STAT 330 Lecture 29
Reading for Today's Lecture: 12.1, 12.2,12.3
Goals of Today's Lecture:
Today's notes
In the model
if the levels of 
are the only levels of interest of
Factor 1 we call Factor 1 (and the 
) a fixed effect. If on the
other hand they are a sample of size I from a population of possible
levels we refer to Factor 1 as a random effect. Often Randomized
Blocks designs have blocks which are regarded as random. For instance
in an experiment where 5 runs of some production process can be run on
a single day we often treat DAY as a blocking factor and then pretend
the days we tried are a sample of possible days.
We call the Model a Fixed Effects model if both factors are fixed, a Random Effects model if both are random and a Mixed model if we have one fixed and one random factor. For mixed models with replicates we get different F tests for main effects. Moreover, the injunction that we test main effects only when there are no interactions is no longer relevant.
END OF CHAPTER 11
Simple Linear Regression and Correlation
Here are two experimental designs used to investigate the relation between two continuous variables.
1: Controlled Experiment: A variable, X is set at values 
and
corresponding values 
of a response variable are measured.
Example: Chapter 12, question 9. x is the "Burner area liberation rate" and
Y is the 
(nitrous oxides) emission rate.
2: A sample of n pairs: We sample a population of n pairs of numbers and
get 
.
Example: we sample 1074 families and measure the Father's height (X) and Son's height (Y) for each family.
In this section our goal is to predict Y from the value of X and not the other way around. We do not treat the variables symmetrically.
Regression Models:
We assume for each observation a model equation of the form
where
is a parameter (or vector of parameters) which describes the
specific relation.
is the error.
Assumptions:
are independent random variables with
mean 0 and variance 
. s are normally distributed.
Definition: The regression is called linear if 
is a linear function of
. (This jargon is used also when each of X and is a vector.)
Our example is Simple Linear Regression.
where the 
are independent mean 0 homoscedastic errors.
(Notice that the map 
is a linear function
of 
. At the same time this model describes a straight line
function of x.
Estimation
Estimation is based on least squares. We choose 
to minimize
To minimize this we take the derivatives 
and
and set them both equal to 0. We get
and
These two equations are called the normal equations usually written in the form
and
The solution is
and
There is an ANOVA table for this least squares analysis based on the identity
where 
is the so-called fitted value namely
.
The quantity
is called the Error Sum of Squares and
the quantity 
is called the Regression
Sum of Squares. We get the following ANOVA table.
In this table the P value is used to test 
. However, for simple
linear regression it is usually better to use a technique which easily provides confidence
intervals for and can be used to test other values of .
Let 
.and note that because 
If the errors are normal so that the 
s are normal then
is normal and we can compute the mean and variance
of 
as follows:
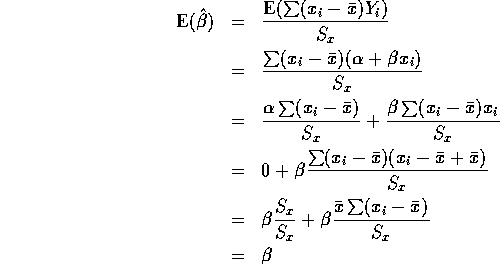
So is unbiased. Next:
