STAT 350: Lecture 29

Power and Sample Size Calculations

Definition: The power function of a test procedure in a model with parameters is

Definition: The non-central distribution t with non-centrality parameter and degrees of freedom is the distribution of

where Z is , U is and Z and U are independent When we get the usual, or central t distribution.

Fact: If a is a vector of length p and is some scalar then

has a non-central t distribution with non-centrality parameter

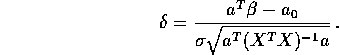
Power of two sided tests from table B 5. Normally computed before experiment based on assumptions about , and .

Sample Size determination

Before an experiment is run it is sensible, if the experiment is costly, to try to work out whether or not it is worth doing. You will only do an experiment if the probability of Type I and II errors are both reasonably low. The simplest case arises when you prespecify a level, say and an acceptable probability of Type II error, say 0.10, for testing a null hypothesis like . Then you need to specify

• The ratio ; this value comes from a physically motivated understanding of what value of the discrepancy would be important to detect and from some understanding of the roughly what values might be reasonable for .
• How the design matrix would depend on the sample size. The easiest thing is to fix some small set of say j values and then use each member of that set say m times so that the aggregate sample size is mk. This gives a non-centrality parameter of the form

  

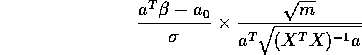
  The value n=mk influences both the row in table B.5 which should be used and the value of . If the solution is large, however, then all the rows in B.5 at the bottom of the table are very similar so that effectively only depends on n; we can then solve for n.

F tests

Simplest example: regression through the origin (no intercept term.)

• Model

  

• Test
• F statistic

  

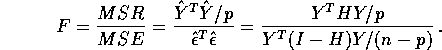
Suppose now that the null hypothesis is false.

• Substitute in F.
• Use HX=X (and so (I-H)X=0).
• Denominator is

  

• So: even when the null hypothesis is false the denominator divided by has the distribution of a on n-p degrees of freedom divided by its degrees of freedom.
• FACT: Numerator and denominator are independent of each other even when the null hypothesis is false.
• Numerator is

  

• Divide by and rewrite this as

  

• has a multivariate normal distribution with mean and variance the identity matrix.

FACT:

If W is a random vector and Q is idempotent with rank p then has a non-central distribution with non-centrality parameter

and p degrees of freedom. This is the same distribution as that of

where the are iid standard normals. An ordinary variable is called central and has .

FACT:

If U and V are independent variables with degrees of freedom and , V is central and U is non-central with non-centrality parameter then

is said to have a non-central F distribution with non-centrality parameter and degrees of freedom and .

POWER CALCULATIONS

• Table B 11 gives powers of F tests for various small numerator degrees of freedom and a range of denominator degrees of freedom
• Must use or .
• In table is our (that is, the square root of what I called the non-centrality parameter divided by the square root of 1 more than the numerator degrees of freedom.)

SAMPLE SIZE CALCULATIONS

• Sometimes done with charts and sometimes with tables; see table B 12.
• This table depends on a quantity

  

  To use the table you specify

  • (one of 0.2, 0.1, 0.05 or 0.01)
  • Power ( in notation of table)- must be one of 0.7, 0.8, 0.9 or 0.95
  • Non-centrality per data point, .

  Then you look up n.

• Realistic specification of difficult in practice.

Examples

POWER of t test: SAND and FIBRE example. See Lecture 11

Consider fitting the model

Compute power of t test of for the alternative . (This is roughly the fitted value. In practice, however, this value needs to be specified before collecting data so you just have to guess or use experience with previous related data sets or work out a value which would make a difference big enough to matter compared to the straight line.)

Need to assume a value for . I take 2.5 - a nice round number near the fitted value. Again, in practice, you will have to make this number up in some reasonable way.

Finally and has to be computed. For the design actually used this is . Now is 2. The power of a two-sided t test at level 0.05 and with 18-4=14 degrees of freedom is 0.46 (from table B 5 page 1346).

Take notice that you need to specify , (or even and ) and the design!

SAMPLE SIZE NEEDED using t test: SAND and FIBRE example.

Now for the same assumed values of the parameters how many replicates of the basic design (using 9 combinations of sand and fibre contents) would I need to get a power of 0.95? The matrix for m replicates of the design actually used is m times the same matrix for 1 replicate. This means that will be 1/m times the same quantiity for 1 replicate. Thus the value of for m replicates will be times the value for our design, which was 2. With m replicates the degrees of freedom for the t-test will be 18m-6. We now need to find a value of m so that in the row in Table B 5 across from 18m-6 degrees of freedom and the column corresponding to

we find 0.95. To simplify we try just assuming that the solution m is quite large abd use the last line of the table. We get between 3 and 4 - say about 3.75. Now set and solve to find m=3.42 which would have to be rounded to 4 meaning a total sample size of . For this value of m the non-centrality parameter is actually 4 (not the target of 3.75 because of rounding) and the power is 0.98. Notice that for this value of m the degrees of freedom for error is 66 which is so far down the table that the powers are not much different from the line.

POWER of F test: SAND and FIBRE example.

Now consider the power of the test that all the higher order terms are 0 in the model

that is the power of the F test of .

You will need to specify the non-centrality parameter for this F test. In general the noncentrality parameter for a F test based on numerator degrees of freedom is given by

This quantity needs to be worked out algebraically for each separate case, however, some general points can be made.

• Write the full model as

  

  and the reduced model as

  

• The Extra SS is the difference between two Error sums of squares. One is for the full model and

  

  because we assume that the FULL model is correct.

• The Error SS for the reduced model is

  

  where . Replace Y by its formula from the full model equation and take expected value. The answer is

  

  where is the rank of . This makes the non-centrality parameter .