is a density.
- (a)
- Let
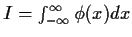 .
Show that
.
Show that
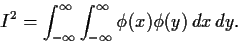
HINT: What is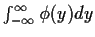 in terms of I.
in terms of I.
- (b)
- Now if
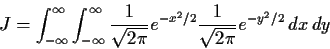
do the double integral J in polar co-ordinates (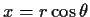 ,
,
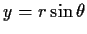 )
to show J=1.
)
to show J=1.
- (c)
- Deduce that
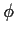 is a density.
is a density.
- (a)
- If XT = (X1,X2,X3) and ZT=(Z1,Z2,Z3) express X in the form AZ+b for a suitable matrix A and vector b.
- (b)
- Show that X is
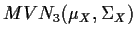 and identify
and identify 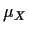 and
and 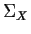 .
.
- (c)
- Let
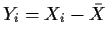 for i=1,2,3 and
for i=1,2,3 and
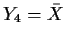 .
Show
that
.
Show
that
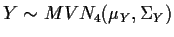 and find
and find 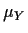 and
and  .
.
- (a)
- Write XTX as a partitioned (3 rows, 3 columns) matrix.
- (b)
- A matrix
![\begin{displaymath}A = \left[\begin{array}{ccc}
A_1 & 0 & 0 \\
0 & A_2 & 0 \\
0 & 0 & A_3
\end{array}\right]
\end{displaymath}](img20.gif)
is called block diagonal. Show that A-1 exists if and only if each Ai-1 exists and that then A-1is block diagonal. - (c)
- Suppose that
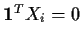 for i=1,2 and
X1TX2=0.
Show that XTX is block diagonal and give a formula for
(XTX)-1.
for i=1,2 and
X1TX2=0.
Show that XTX is block diagonal and give a formula for
(XTX)-1.
- (d)
- Suppose
![$\beta^T = [ \beta_0\vert \beta_1^T\vert\beta_2^T]$](img22.gif) is partitioned
to conform with the partitioning of X (that is
is partitioned
to conform with the partitioning of X (that is 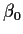 is a scalar
and
is a scalar
and 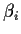 is a column vector of length pi for i=1,2.
Let
is a column vector of length pi for i=1,2.
Let
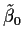 be obtained by fitting
be obtained by fitting
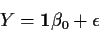
by least squares,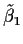 be obtained by fitting
be obtained by fitting
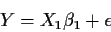
and similarly for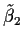 .
Let
.
Let 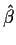 be the usual
least squares estimate for
be the usual
least squares estimate for
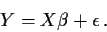
Show that![$\hat\beta^T = [ \tilde\beta_0\vert \tilde\beta_1^T\vert\tilde\beta_2^T]$](img32.gif) .
.
- (e)
- Let
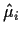 be the vectors of fitted values corresponding to the
estimates
be the vectors of fitted values corresponding to the
estimates
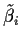 for i=1,2,3. Show that for
for i=1,2,3. Show that for 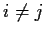 we have
we have
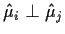 .
.
- (f)
- For the design matrix Xb of the first assignment identify X1 and X2 and verify the orthogonality condition of this problem.