Postscript version of these notes

STAT 350: Lecture 31

Heteroscedastic Errors

If plots and/or tests show that the error variances $\sigma_i^2 = Var(\epsilon_i)$ depend on i there are several standard approaches to fixing the problem, depending on the nature of the dependence.

• If the variances are known except for a constant factor then we may write $\sigma_i^2 =\sigma^2/w_i$ and use a technique called weighted least squares. (See Chapter 10 in the text.)

  This usually arises realistically in the following situations:

  • Y_i is an average of n_i measurements where you know n_i. Then w_i=n_i.

  • Plots suggest that $\sigma_i^2$ might be proportional to some power of some covariate: $\sigma_i^2 = k x_i^\gamma$. Then $w_i=x_i^{-\gamma}$.

• If the variances are thought to depend on the mean of Y_i then two standard approaches are available:

  • The older approach is transformation. We compute Y_i^*=g(Y_i) for some function g like the logarithm or square root. Then we regress Y_i^* on the covariates. This approach sometimes works for skewed response variables like income; after transformation we occasionally find the errors are more nearly normal, more homoscedastic and that the model is simpler. See page 130ff and check under transformations and Box-Cox in the index.

  • The newer approach is to use a generalized linear model; see STAT 402.

  • Transformation uses the model
    
    $$E(g(Y_i)) = x_i^T\beta$$
    
    
    while generalized linear models use
    
    $$g(E(Y_i)) = x_i^T\beta \,$$
    
    
    Generally the latter approach offers more flexibility since it is then possible to model the variance as a general function of the mean while for transformation followed by ordinary least squares the transformed data must follow a homoscedastic linear model.

• It is also possible to use a hybrid approach in which the parameters are estimated by least squares but inference (estimation of standard errors, testing, confidence intervals) are based on a model in which the errors may be heteroscedastic.

Weighted Least Squares

If

$$E(Y_i) = x_i^T\beta$$

and

$$Var(Y_i) = \sigma^2/w_i$$

and the errors are independent with normal distributions then the likelihood is

$$\prod_{i=1}^n \frac{\sqrt{w_i}}{\sqrt{2\pi}\sigma}\exp\left[ -\frac{w_i}{2\sigma^2}(Y_i-x_i^T\beta)^2\right]$$

To choose $\beta$ to maximize this likelihood we minimize the quantity

$$\sum_{i=1}^n w_i (Y_i-x_i^T\beta)^2 \,.$$

The process is called weighted least squares.

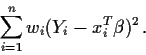
Algebraically it is easy to see how to do the minimization. Rewrite the quantity to be minimized as

$$\sum_{i=1}^n \left[ w_i^{1/2} Y_i - ( w_i^{1/2}x_i)^T\beta\right]^2 \, .$$

This is just an ordinary least squares problem with the response variable being

Y_i^* = w_i^1/2 Y_i

and the covariates being

$$x_i^* = w_i^{1/2}x_i \, .$$

The calculation can be written in matrix form. If W^1/2 is a diagonal matrix with w_i^1/2 in the ith diagonal position then put Y^* = W^1/2Y and X^* =W^1/2X. Then

$$Y=X\beta+\epsilon$$

becomes

$$Y^* = X^*\beta = W^{1/2}\epsilon$$

If $\epsilon$ had mean 0, independent entries and $Var(\epsilon_i) = \sigma^2/w_i$ then $\epsilon^* = W^{1/2}\epsilon$ has mean 0, independent entries $\epsilon_i^* = w_i^{1/2}\epsilon$ and $Var(\epsilon_i^*) = \sigma^2$ so that ordinary multiple regression theory applies. The estimate of $\beta$ is

$$\hat\beta_w = \left[(X^*)^TX^*\right]^{-1} (X^*)^TY^* = (X^TWX)^{-1}X^TWY$$

where now W=W^1/2W^1/2 is a diagonal matrix with w_i on the diagonal. This estimate is unbiased and has variance covariance matrix

$$\sigma^2\left[(X^*)^TX^*\right]^{-1} = \sigma^2(X^TWX)^{-1}\, .$$

Example

It is possible to do weighted least squares in SAS fairly easily. As an example we consider using the SENIC data set taking the variance of RISK to be proportional to 1/CENSUS. (Motivation: RISK is an estimated proportion; variance of a Binomial proportion is inversely proportional to the sample size. This makes the weight just CENSUS.

proc reg  data=scenic;
  model Risk = Culture Stay Nratio Chest Facil;
  weight Census;
run ;

EDITED OUTPUT (Complete output)

Dependent Variable: RISK                                               
                        Analysis of Variance
                        Sum of         Mean
  Source       DF      Squares       Square      F Value       Prob>F
  Model         5  12876.94280   2575.38856       17.819       0.0001
  Error       107  15464.46721    144.52773
  C Total     112  28341.41001
      Root MSE      12.02197     R-square       0.4544
      Dep Mean       4.76215     Adj R-sq       0.4289
      C.V.         252.44833
                              Parameter Estimates
                    Parameter      Standard    T for H0:               
   Variable  DF      Estimate         Error   Parameter=0    Prob > |T|
   INTERCEP   1      0.468108    0.62393433         0.750        0.4547
   CULTURE    1      0.030005    0.00891714         3.365        0.0011
   STAY       1      0.237420    0.04444810         5.342        0.0001
   NRATIO     1      0.623850    0.34803271         1.793        0.0759
   CHEST      1      0.003547    0.00444160         0.799        0.4263
   FACIL      1      0.008854    0.00603368         1.467        0.1452

EDITED OUTPUT FOR UNWEIGHTED CASE (Complete output)

Dependent Variable: RISK                                               
                           Analysis of Variance
                              Sum of         Mean
  Source       DF      Squares       Square      F Value       Prob>F
  Model         5    108.32717     21.66543       24.913       0.0001
  Error       107     93.05266      0.86965
  C Total     112    201.37982
      Root MSE       0.93255     R-square       0.5379
      Dep Mean       4.35487     Adj R-sq       0.5163
      C.V.          21.41399
                        Parameter Estimates
                 Parameter      Standard    T for H0:               
  Variable  DF      Estimate         Error   Parameter=0    Prob > |T|
  INTERCEP   1     -0.768043    0.61022741        -1.259        0.2109
  CULTURE    1      0.043189    0.00984976         4.385        0.0001
  STAY       1      0.233926    0.05741114         4.075        0.0001
  NRATIO     1      0.672403    0.29931440         2.246        0.0267
  CHEST      1      0.009179    0.00540681         1.698        0.0925
  FACIL      1      0.018439    0.00629673         2.928        0.0042

• Notice many changes in significance levels.

• Weighted model would fail diagnostic tests - it would be clearly heteroscedastic.

• Can compute standardized residuals and so on from starred variables as usual.

Transformation

Sometimes the response variable will have a distribution which makes it likely that the errors will be not very normal and that the errors will not be homoscedastic. Typical examples:

• Binary Response Data: the Y_i are either just Bernoulli variables (0 or 1) or Binomial variables:.

  Example: For each of the doses $d_1, \ldots , d_p$ a number of animals $n_1, \ldots , n_p$ are treated with the corresponding dose of some drug. The number, Y, dying at dose d is Binomial with parameter h(d).

• Count Data: the Y_i are counts of the number of times something happens such as the number of traffic accidents at a corner, or cases of leukemia in a region. Typically we might suppose the Y_i to have Poisson distributions.

• Skewed continuous data: the Y_i seem to come from some skewed continuous distribution -- times to recurrence of a disease after surgery might be an example.

The traditional analysis method is to try transformation:

• For Binomial Y_i we use the arc sin transformation:
  
  $$Y_i^* = 2 \arcsin \sqrt{Y_i/n_i}$$
  
  

• For Poisson Y_i we take square roots $Y_i^*=\sqrt{Y_i}$. This is appropriate whenever we think $\sigma_i^2$ is proportional to $\mu_i=E(Y_i)$.

• For data such as money where percentage changes might be a sensible way to think about the variable take logarithms, $Y_i^*=\log{Y_i}$. This is useful if $\sigma_i$ is proportional to $\mu_i$.

• Look up Box-Cox transformation to estimate the transformation.

BIGGEST PROBLEM If the model was linear before transformation then it will not be linear after transformation.