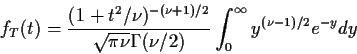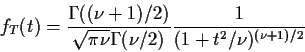Goals of Today's Lecture:
Review of end of last time
I defined independent events and then independent random variables:
Def'n: Ai,
![]() independent:
independent:
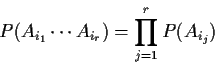
Def'n: Rvs
![]() independent:
independent:
Theorem:
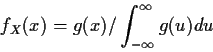
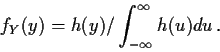
Proof:
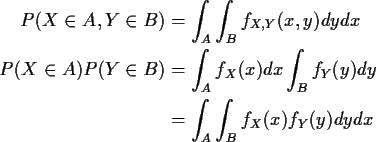
![\begin{displaymath}\int_A\int_B [ f_{X,Y}(x,y) - f_X(x)f_Y(y) ]dydx = 0
\end{displaymath}](img16.gif)
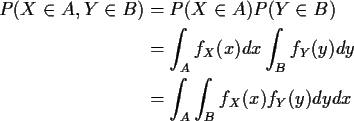

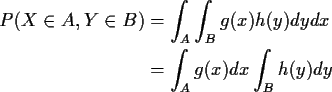
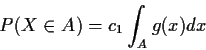
Theorem: If
![]() are independent and
Yi =gi(Xi) then
are independent and
Yi =gi(Xi) then
![]() are independent.
Moreover,
are independent.
Moreover,
![]() and
and
![]() are
independent.
are
independent.
Def'n:
P(A|B) = P(AB)/P(B) if
![]() .
.
Def'n: For discrete X and Y the conditional
probability mass function of Y given X is
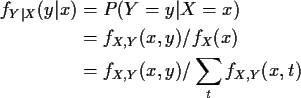
For absolutely continuous X
P(X=x) = 0 for all
x. What is P(A| X=x) or
fY|X(y|x)?
Solution: use limit
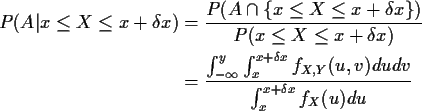

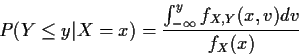
Def'n:
![]() iff
iff
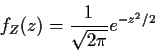
Def'n:
![]() iff
iff
![]() (a column vector for later use) with the
Zi independent and each
(a column vector for later use) with the
Zi independent and each
![]() .
.
In this case according to our theorem
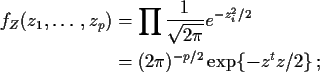
superscript t denotes matrix transpose.
Def'n: ![]() has a multivariate normal distribution if it
has the same distribution as
has a multivariate normal distribution if it
has the same distribution as ![]() for some
for some
![]() ,
some
,
some
![]() matrix of constants A and
matrix of constants A and
![]() .
.
If the matrix A is singular then X will not have a density. If A is
invertible then we can derive the multivariate normal density
by the change of variables formula:
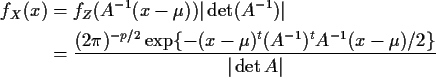
For which vectors ![]() and matrices
and matrices ![]() is this a density?
Any
is this a density?
Any ![]() but if
but if ![]() then
then
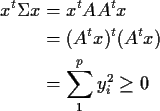
where y=At x. Inequality strict except for y=0 which
is equivalent to x=0. Thus ![]() is a positive definite symmetric
matrix. Conversely, if
is a positive definite symmetric
matrix. Conversely, if ![]() is a positive definite symmetric matrix
then there is a square invertible matrix A such that
is a positive definite symmetric matrix
then there is a square invertible matrix A such that
![]() so that
there is a
so that
there is a
![]() distribution. (A can be found
via the Cholesky decomposition, e.g.)
distribution. (A can be found
via the Cholesky decomposition, e.g.)
More generally X has multivariate normal distribution
if it has the same distribution as ![]() (no
restriction that A be non-singular). When A is singular X will not
have a density:
(no
restriction that A be non-singular). When A is singular X will not
have a density: ![]() such that
such that
![]() ;
X is confined to a hyperplane. Still
true that the distribution of X depends only on the matrix
;
X is confined to a hyperplane. Still
true that the distribution of X depends only on the matrix
![]() :
if
AAt = BBt then
:
if
AAt = BBt then ![]() and
and
![]() have the same distribution.
have the same distribution.
Properties of the MVN distribution
1: All margins are multivariate normal: if
![\begin{displaymath}X = \left[\begin{array}{c} X_1\\ X_2\end{array} \right]
\end{displaymath}](img67.gif)
![\begin{displaymath}\mu = \left[\begin{array}{c} \mu_1\\ \mu_2\end{array} \right]
\end{displaymath}](img68.gif)
![\begin{displaymath}\Sigma = \left[\begin{array}{cc} \Sigma_{11} & \Sigma_{12}
\\
\Sigma_{21} & \Sigma_{22} \end{array} \right]
\end{displaymath}](img69.gif)
2: All conditionals are normal: the conditional distribution of X1given X2=x2 is
![]()
3:
![]() :
affine
transformation of MVN is normal.
:
affine
transformation of MVN is normal.
Theorem:
Suppose
![]() are independent
are independent
![]() random
variables.
Then
random
variables.
Then
Proof: Let
![]() .
Then
.
Then
![]() are
independent N(0,1) so
are
independent N(0,1) so
![]() is multivariate
standard normal. Note that
is multivariate
standard normal. Note that
![]() and
and
![]() Thus
Thus
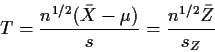
So: reduced to ![]() and
and ![]() .
.
Step 1: Define
![\begin{displaymath}Y =\left[\begin{array}{cccc}
\frac{1}{\sqrt{n}} &
\frac{1}{\s...
...in{array}{c}
Z_1 \\
Z_2 \\
\vdots
\\
Z_n
\end{array}\right]
\end{displaymath}](img91.gif)
![\begin{align*}MM^t & = \left[\begin{array}{c\vert cccc}
1 & 0 & 0 & \cdots & 0 \...
...egin{array}{c\vert c}
1 & 0
\\
\hline
\\
0 & Q
\end{array}\right]
\end{align*}](img94.gif)
Solve for Z from Y:
Zi = n-1/2Y1+Yi+1for
![]() .
Use the identity
.
Use the identity
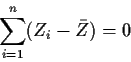
![\begin{displaymath}\Sigma^{-1} \equiv (MM^t)^{-1} =
\left[\begin{array}{c\vert c}
1 & 0
\\
\hline
\\
0 & Q^{-1}
\end{array}\right]
\end{displaymath}](img98.gif)
Now we use the change of variables formula to compute the density
of Y. Let ![]() denote vector whose
entries are
denote vector whose
entries are
![]() .
Note that
.
Note that
![\begin{align*}f_Y(y) =& (2\pi)^{-n/2} \exp[-y^t\Sigma^{-1}y/2]/\vert\det M\vert
...
...^{-(n-1)/2}\exp[-{\bf y}_2^t Q^{-1} {\bf y_2}/2]}{\vert\det M\vert}
\end{align*}](img102.gif)
Note: ftn of y1 times a
ftn of
![]() .
Thus
.
Thus
![]() is independent of
is independent of
![]() .
Since sZ2 is a function of
.
Since sZ2 is a function of
![]() we see that
we see that
![]() and
sZ2 are independent.
and
sZ2 are independent.
Also, density of Y1 is a multiple of the function of y1 in
the factorization above. But factor is standard normal
density so
![]() .
.
First 2 parts done. Third part is
a homework exercise. Derivation of the ![]() density:
density:
Suppose
![]() are independent N(0,1). Define
are independent N(0,1). Define
![]() distribution to be that of
distribution to be that of
![]() .
Define angles
.
Define angles
![]() by
by
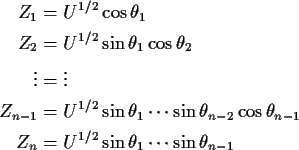
(Spherical co-ordinates in n dimensions. The ![]() values run
from 0 to
values run
from 0 to ![]() except last
except last ![]() from 0 to
from 0 to ![]() .)
Derivative formulas:
.)
Derivative formulas:
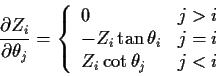
![\begin{displaymath}\left[\begin{array}{ccc}
\frac{\cos\theta_1}{2\sqrt{U}}
&
-U^...
...theta_2
&
U^{1/2} \sin\theta_1\cos\theta_2
\end{array}\right]
\end{displaymath}](img117.gif)

Fourth part is consequence of
first 3 parts and def'n of ![]() distribution, namely,
distribution, namely,
![]() if it has same distribution
as
if it has same distribution
as
Derive density of T in this definition:
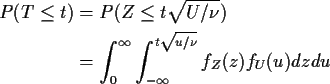
Differentiate wrt t by
differentiating inner integral:
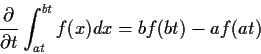
![\begin{displaymath}\frac{d}{dt} P(T \le t) =
\int_0^\infty f_U(u) \sqrt{u/\nu}\frac{\exp[-t^2u/(2\nu)]}{\sqrt{2\pi}} du
\end{displaymath}](img138.gif)
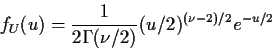
![\begin{displaymath}f_T(t) = \int_0^\infty \frac{(u/2)^{(\nu-1)/2}}{2\sqrt{\pi\nu}\Gamma(\nu/2)}
\exp[-u(1+t^2/\nu)/2]du
\end{displaymath}](img140.gif)