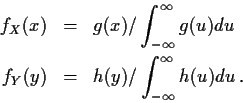Reading: Ch. 1, 2 and 4 of Casella and Berger.
Goals of Today's Lecture:
Today's notes
So far: defined probability space, real and vector valued random variables cdfs in R1 and Rp, discrete densities and densities for random variables with absolutely continuous distributions.
Started distribution theory: for Y=g(X) with X and Y
each real valued
![\begin{eqnarray*}P(Y \le y) & = & P(g(X) \le y)
\\
& = & P(X \in g^{-1}(-\infty,y])
\\
& = & P(X \in \{x: g(x) \le y\} )
\end{eqnarray*}](img2.gif)
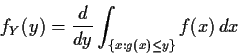
Method 2: Change of variables.
Assume g is one to one.
I do: g is increasing and differentiable.
Interpretation of density (based on density = ![]() ):
):
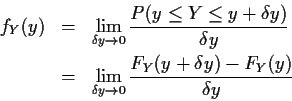
Remark: For g decreasing
![]() but Then
the interval
but Then
the interval
![]() is really
is really
![]() so
that
so
that
![]() .
In both cases this amounts to the formula
.
In both cases this amounts to the formula
Example:
![]() or
or
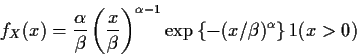
Let ![]() or
or
![]() .
Solve
.
Solve ![]() :
:
![]() or
g-1(y) = ey. Then
or
g-1(y) = ey. Then
![]() and
and
![]() Hence
Hence
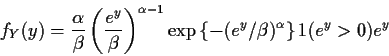
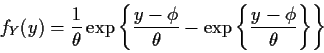
Simplest multivariate problem:
![]() ,
Y=X1 (or in general any Xj).
,
Y=X1 (or in general any Xj).

![]() is the marginal density of
is the marginal density of
![]() and fXthe joint density of X but
they are both just densities.
``Marginal'' just to
distinguish from the joint density of X.
and fXthe joint density of X but
they are both just densities.
``Marginal'' just to
distinguish from the joint density of X.
Example The function
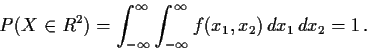
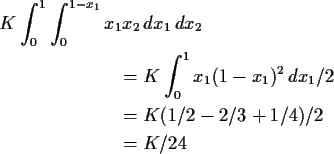
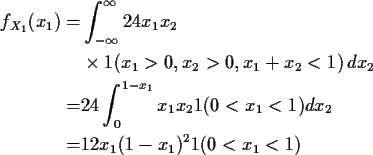
General problem has
![]() with
with
![]() .
.
Case 1: q>p. Y won't have density for ``smooth'' g. Y will have a singular or discrete distribution. Problem rarely of real interest. (But, e.g., residuals have singular distribution.)
Case 2: q=p. We use a change of variables formula which generalizes the one derived above for the case p=q=1. (See below.)
Case 3: q < p.
Pad out Y-add on p-q more variables (carefully chosen)
say
![]() .
Find functions
.
Find functions
![]() .
Define for
.
Define for ![]() ,
,
![]() and
and
![]() Choose gi so that we can use change of variables on
Choose gi so that we can use change of variables on
![]() to compute fZ. Find fYby integration:
to compute fZ. Find fYby integration:
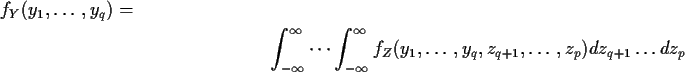
Suppose
![]() with
with ![]() having density fX.
Assume g is a one to one (``injective") map, that is,
g(x1) = g(x2) if and only if x1 = x2.
Find fY as follows:
having density fX.
Assume g is a one to one (``injective") map, that is,
g(x1) = g(x2) if and only if x1 = x2.
Find fY as follows:
Step 1: Solve for x in terms of y: x=g-1(y).
Step 2: Use basic equation:
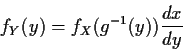
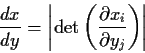
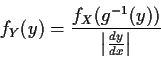
![\begin{displaymath}\left\vert\frac{dy}{dx}\right\vert =
\left\vert \mbox{det} \...
...rac{\partial y_p}{\partial x_p}
\end{array} \right]\right\vert
\end{displaymath}](img63.gif)
Example: The density
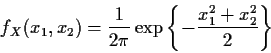
Solve for x in terms of y:
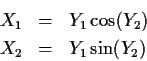
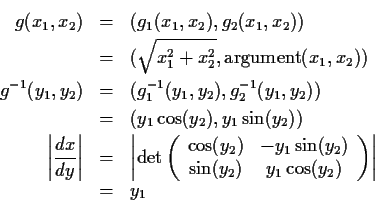
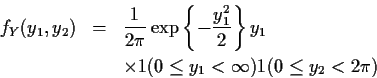
Next: marginal densities of Y1, Y2?
Factor fY as
fY(y1,y2) = h1(y1)h2(y2) where
Then
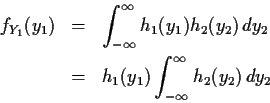
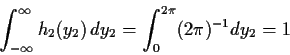
Note: We show below factorization of density is equivalent to independence.
So far density of X specified explicitly. Often modelling leads to a specification in terms of marginal and conditional distributions.
Def'n: Events A and B are independent if
Def'n: Ai,
![]() are independent if
are independent if
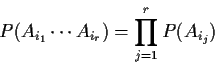
Example: p=3
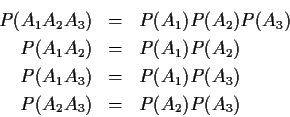
Def'n: X and Y are
independent if
Def'n:
![]() are
independent if
are
independent if
Theorem