


Postscript version of this page
STAT 801: Mathematical Statistics
Moment Generating Functions
Def'n: The moment generating function of a real valued 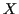 is
is
defined for those real 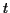 for which the expected value is finite.
for which the expected value is finite.
Def'n: The moment generating function of 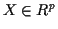 is
is
defined for those vectors 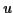 for which the expected value is finite.
for which the expected value is finite.
Formal connection to moments:
Sometimes can find power series expansion of
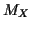 and read off the moments of
and read off the moments of 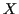 from the coefficients of
from the coefficients of
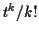 .
.
Theorem: If 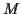 is finite for all
is finite for all
![$ t \in [-\epsilon,\epsilon]$](img13.gif) for some
for some
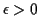 then
then
- Every moment of
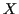 is finite.
is finite.
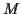 is
is 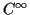 (in fact
(in fact 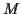 is analytic).
is analytic).
-
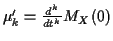 .
.
Note: 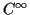 means has continuous derivatives of all orders. Analytic
means has convergent power series expansion in neighbourhood of each
means has continuous derivatives of all orders. Analytic
means has convergent power series expansion in neighbourhood of each
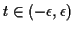 .
.
The proof, and many other facts about mgfs, rely on techniques
of complex variables.
MGFs and Sums
If
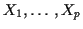 are independent and
are independent and
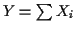 then
the moment generating function of
then
the moment generating function of 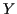 is the product of those
of the individual
is the product of those
of the individual 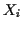 :
:
or
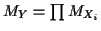 .
.
Note: also true for multivariate 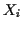 .
.
Problem: power series expansion of 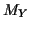 not
nice function of expansions of individual
not
nice function of expansions of individual 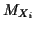 .
.
Related fact: first 3 moments
(meaning 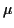 ,
, 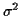 and
and 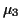 ) of
) of 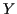 are sums of those
of the
are sums of those
of the 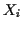 :
:
but
It is possible, however, to replace the moments by other objects called
cumulants which do add up properly. The way to define them relies
on the observation that the log of the mgf of 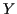 is the sum of the logs
of the mgfs of the
is the sum of the logs
of the mgfs of the 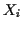 . We define the cumulant generating function of a
variable
. We define the cumulant generating function of a
variable 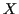 by
by
Then
The mgfs are all positive so that the cumulative generating
functions are defined wherever the mgfs are. This means we can
give a power series expansion of 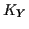 :
We call the
:
We call the 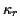 the cumulants of
the cumulants of 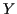 and observe
and observe
To see the relation between cumulants and moments proceed as follows:
the cumulant generating function is
To compute the power series expansion we thing of the quantity in
![$ [\ldots]$](img45.gif) as
as 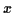 and expand
When you stick in the power series
you have to expand out the powers of
and expand
When you stick in the power series
you have to expand out the powers of 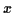 and collect together like terms.
For instance,
and collect together like terms.
For instance,
Now gather up the terms. The power 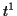 occurs only in
occurs only in 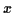 with
coefficient
with
coefficient 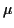 . The power
. The power 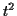 occurs in
occurs in 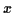 and in
and in 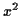 and so on.
Putting these together gives
and so on.
Putting these together gives
Comparing coefficients to 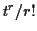 we see that
we see that
Check the book by Kendall and Stuart (or the new version
called Kendall's Theory of Advanced Statistics by Stuart and Ord)
for formulas for larger orders 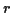 .
.
Example: If
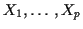 are independent and
are independent and 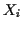 has a
has a
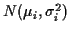 distribution
then
distribution
then
This makes the cumulant generating function
and the cumulants are
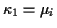 ,
,
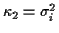 and every other
cumulant is 0. The cumulant generating function for
and every other
cumulant is 0. The cumulant generating function for
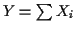 is
which is the cumulant generating function of
is
which is the cumulant generating function of
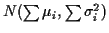 .
.
Example: I am having you derive the moment and cumulant generating function
and all the moments of a Gamma rv. Suppose that
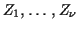 are independent
are independent
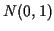 rvs. Then we have defined
rvs. Then we have defined
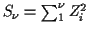 to have a
to have a  distribution. It is easy to check
distribution. It is easy to check 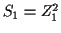 has density
has density
and then the mgf of 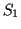 is
It follows that
which you will show in homework is the moment generating function of
a Gamma
is
It follows that
which you will show in homework is the moment generating function of
a Gamma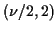 rv. This shows that the
rv. This shows that the
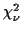 distribution has
the Gamma
distribution has
the Gamma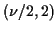 density which is
density which is
Example: The Cauchy density is
the corresponding moment generating function is
which is 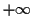 except for
except for 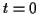 where we get 1.
This mgf is exactly the mgf of every
where we get 1.
This mgf is exactly the mgf of every 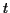 distribution
so it is not much use for distinguishing such distributions.
The problem is that these distributions do not have infinitely
many finite moments.
distribution
so it is not much use for distinguishing such distributions.
The problem is that these distributions do not have infinitely
many finite moments.
This observation has led to the development of a substitute for the mgf
which is defined for every distribution, namely, the characteristic function.
Characteristic Functions
Definition: The characteristic function of a real rv 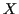 is
is
where
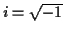 is the imaginary unit.
is the imaginary unit.
Aside on complex arithmetic.
Complex numbers: add
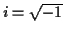 to the
real numbers.
to the
real numbers.
Require all the usual rules of algebra to work.
So:
if 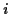 and any real numbers
and any real numbers 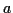 and
and 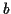 are to be complex numbers then so
must
be
are to be complex numbers then so
must
be 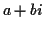 .
.
Multiplication:
If we multiply a complex number 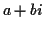 with
with 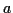 and
and 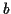 real by
another such number, say
real by
another such number, say 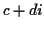 then the usual rules of arithmetic
(associative,
commutative and distributive laws) require
then the usual rules of arithmetic
(associative,
commutative and distributive laws) require
so this is precisely how we define multiplication.
Addition: follow usual rules to get
Additive inverses:
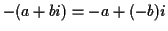 .
.
Multiplicative inverses:
Division:
Notice: usual rules of arithmetic don't require any more numbers
than
where 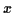 and
and 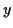 are real.
are real.
Now look at transcendental functions. For real 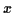 we know
we know
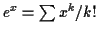 so
our insistence on the usual rules working means
so
our insistence on the usual rules working means
and we need to know how to compute 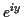 . Remember in what follows that
. Remember in what follows that
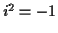 so
so 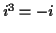 ,
, 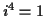
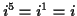 and so on. Then
and so on. Then
We can thus write
Identify 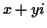 with the
corresponding point
with the
corresponding point 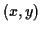 in the plane. Picture the complex numbers
as forming a plane.
in the plane. Picture the complex numbers
as forming a plane.
Now every point in the plane can be written in polar co-ordinates as
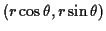 and comparing this with our formula for the
exponential we see we can write
and comparing this with our formula for the
exponential we see we can write
for an angle
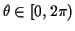 .
.
Multiplication revisited:
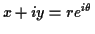 ,
,
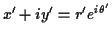 .
.
We will need from time to time a couple of other definitions:
Definition: The modulus of 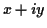 is
is
Definition: The complex conjugate of 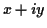 is
is
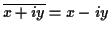 .
.
Some identities:
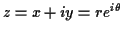 and
and
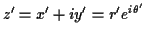 .
.
Notes on calculus with complex variables. Essentially the usual rules apply so,
for example,
We will (mostly) be doing only integrals over the real line; the theory of integrals
along paths in the complex plane is a very important part of mathematics, however.
FACT: (not use explicitly in course). If
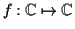 is
differentiable then
is
differentiable then 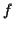 is analytic (has power series expansion).
is analytic (has power series expansion).
End of Aside
Characteristic Functions
Definition: The characteristic function of a real rv 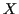 is
is
where
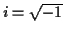 is the imaginary unit.
is the imaginary unit.
Since
we find that
Since the trigonometric functions are bounded by 1 the expected values must
be finite for all 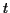 and this is precisely the reason for using
characteristic rather than moment generating functions in probability
theory courses.
and this is precisely the reason for using
characteristic rather than moment generating functions in probability
theory courses.
Theorem 1
For any two real rvs
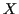
and
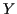
the following are
equivalent:
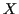 and
and 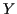 have the same distribution, that is, for any (Borel)
set
have the same distribution, that is, for any (Borel)
set 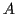 we have
we have
-
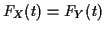 for all
for all 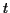 .
.
-
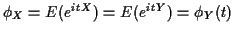 for all real
for all real 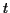 .
.
Moreover, all of these are implied if there is a positive
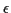
such
that for all
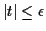
Theorem 2
For any two real rvs
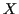
and
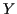
the following are
equivalent:
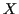 and
and 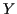 have the same distribution, that is, for any (Borel)
set
have the same distribution, that is, for any (Borel)
set 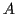 we have
we have
-
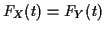 for all
for all 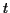 .
.
-
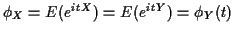 for all real
for all real 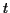 .
.
Moreover, all of these are implied if there is a positive
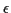
such
that for all
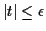
Inversion
Previous theorem is non-constructive characterization.
Can get from 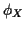 to
to 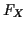 or
or 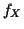 by inversion.
See homework for basic inversion formula:
by inversion.
See homework for basic inversion formula:
If 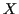 is a random variable taking only integer values then
for each integer
is a random variable taking only integer values then
for each integer 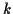
The proof proceeds from the formula
Now suppose that 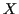 has a continuous bounded density
has a continuous bounded density 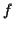 . Define
. Define
where ![$ [a]$](img171.gif) denotes the integer part (rounding down to the next smallest
integer). We have
denotes the integer part (rounding down to the next smallest
integer). We have
Make the substitution 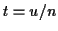 , and get
Now, as
, and get
Now, as
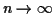 we have
(by the dominated convergence theorem - the dominating random variable
is just the constant 1). The range of integration converges to the whole
real line and if
we have
(by the dominated convergence theorem - the dominating random variable
is just the constant 1). The range of integration converges to the whole
real line and if 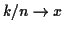 we see that the left hand side converges to
the density
we see that the left hand side converges to
the density 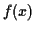 while the right hand side converges to
which gives the inversion formula
Many other such formulas are available to compute things like
while the right hand side converges to
which gives the inversion formula
Many other such formulas are available to compute things like
 and so on.
and so on.
All such formulas are sometimes referred to as Fourier inversion formulas;
the characteristic function itself is sometimes called the Fourier
transform of the distribution or cdf or density of  .
.
Inversion of the Moment Generating Function
MGF and characteristic function related
formally:
When 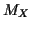 exists this relationship is not merely formal; the
methods of complex variables mean there is a ``nice'' (analytic)
function which is
exists this relationship is not merely formal; the
methods of complex variables mean there is a ``nice'' (analytic)
function which is 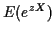 for any complex
for any complex
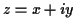 for which
for which 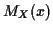 is finite.
is finite.
SO: there is an inversion formula for 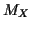 using a
complex contour integral:
using a
complex contour integral:
If 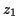 and
and 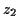 are two
points in the complex plane and
are two
points in the complex plane and 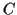 a path between these two points we
can define the path integral
a path between these two points we
can define the path integral
by the methods of line integration.
Do algebra with
such integrals via usual theorems of calculus.
The Fourier
inversion formula was
so replacing 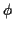 by
by 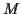 we get
If we just substitute
we get
If we just substitute 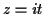 then we find
where the path
then we find
where the path 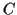 is the imaginary axis.
Methods of complex integration permit us to replace
is the imaginary axis.
Methods of complex integration permit us to replace 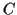 by any other path which starts and ends at the same place. Sometimes
can choose path to make it easy to do the integral
approximately; this is what saddlepoint approximations are.
Inversion formula is called the inverse Laplace transform; the mgf is
also called the Laplace transform of the distribution or cdf or
density.
by any other path which starts and ends at the same place. Sometimes
can choose path to make it easy to do the integral
approximately; this is what saddlepoint approximations are.
Inversion formula is called the inverse Laplace transform; the mgf is
also called the Laplace transform of the distribution or cdf or
density.
Applications of Inversion
1): Numerical calculations
Example: Many statistics have a distribution which is approximately that
of
where the 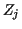 are iid
are iid 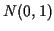 . In this case
. In this case
Imhof ( Biometrika, 1961) gives a simplification of the Fourier
inversion formula for
which can be evaluated numerically:
Multiply
top and bottom by the complex conjugate of the denominator:
The complex number
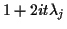 is
is
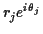 where
where
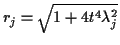 and
and
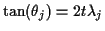 .
This allows us to rewrite
or
Assemble this to give
where
and
.
This allows us to rewrite
or
Assemble this to give
where
and
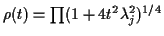 .
But
We can now collect up the real part of the resulting integral to
derive the formula given by Imhof. I don't produce the details here.
.
But
We can now collect up the real part of the resulting integral to
derive the formula given by Imhof. I don't produce the details here.
2): The central limit theorem (in some versions) can be deduced from
the Fourier inversion formula:
if
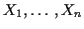 are iid with mean 0 and variance 1 and
are iid with mean 0 and variance 1 and
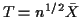 then with
then with 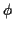 denoting the characteristic function of
a single
denoting the characteristic function of
a single 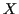 we have
we have
But now
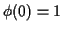 and
So
and
So
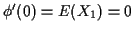 .
Similarly
so that
It now follows that
.
Similarly
so that
It now follows that
With care we can then apply the Fourier inversion formula and
get
where
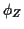 is the characteristic function of a standard normal variable
is the characteristic function of a standard normal variable
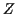 . Doing the integral we find
so that
which is a standard normal random variable.
. Doing the integral we find
so that
which is a standard normal random variable.
This proof of the central limit theorem is not terribly general
since it requires 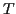 to have a bounded continuous density. The central
limit theorem itself is a statement about cdfs not densities and is
to have a bounded continuous density. The central
limit theorem itself is a statement about cdfs not densities and is
3) Saddlepoint approximation from
MGF inversion formula
(limits of integration indicate contour
integral running up imaginary axis.)
Replace contour (using complex variables) with
line 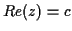 . (
. (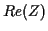 denotes the real part
of
denotes the real part
of 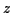 , that is,
, that is, 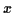 when
when 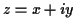 with
with 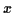 and
and 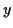 real.) Must choose
real.) Must choose
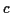 so that
so that
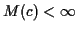 .
Rewrite inversion formula using cumulant generating function
.
Rewrite inversion formula using cumulant generating function
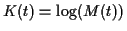 :
Along the contour in question we have
:
Along the contour in question we have 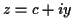 so we can think of the
integral as being
Now do a Taylor expansion of the exponent:
Ignore the higher order terms and select a
so we can think of the
integral as being
Now do a Taylor expansion of the exponent:
Ignore the higher order terms and select a 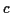 so that the first derivative
vanishes. Such a
so that the first derivative
vanishes. Such a 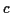 is a saddlepoint. We get the formula
The integral is just a normal density calculation and gives
is a saddlepoint. We get the formula
The integral is just a normal density calculation and gives
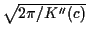 . The saddlepoint approximation is
. The saddlepoint approximation is
Essentially the same idea lies at the heart of the proof of
Sterling's approximation to the factorial function:
The exponent is maximized when 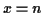 . For
. For 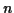 large
we approximate
large
we approximate
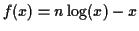 by
and choose
by
and choose 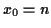 to make
to make
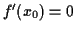 . Then
Substitute
. Then
Substitute
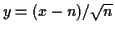 to get the approximation
or
to get the approximation
or
This tactic is called Laplace's method. Note that I am being very sloppy about the
limits of integration; to do the thing properly you have to prove that
the integral over  not near
not near  is negligible.
is negligible.



Postscript version of this page
Richard Lockhart
2001-01-21
![]() is
is
![]() is
is
![$\displaystyle = \sum_{k=0}^\infty E[(tX)^k]/k!$](img8.gif)
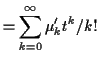
![]() is finite for all
is finite for all
![]() for some
for some
![]() then
then
![]() means has continuous derivatives of all orders. Analytic
means has convergent power series expansion in neighbourhood of each
means has continuous derivatives of all orders. Analytic
means has convergent power series expansion in neighbourhood of each
![]() .
.
![]() are independent and
are independent and
![]() then
the moment generating function of
then
the moment generating function of ![]() is the product of those
of the individual
is the product of those
of the individual ![]() :
:
![]() .
.
![]() not
nice function of expansions of individual
not
nice function of expansions of individual ![]() .
.
![]() ,
, ![]() and
and ![]() ) of
) of ![]() are sums of those
of the
are sums of those
of the ![]() :
:
![$\displaystyle E[(Y-E(Y))^4] =
\sum \{E[(X_i-E(X_i))^4] -3E^2[(X_i-E(X_i))^2]\}
+ 3 \left\{\sum E[(X_i-E(X_i))^2]\right\}^2\, .
$](img35.gif)
![]() is the sum of the logs
of the mgfs of the
is the sum of the logs
of the mgfs of the ![]() . We define the cumulant generating function of a
variable
. We define the cumulant generating function of a
variable ![]() by
by
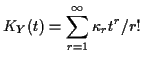
![\begin{multline*}
K(t) =
\\
\mu t + [\mu_2^\prime -\mu^2]t^2/2 \\
+ [\mu_3^\p...
...(\mu_2^\prime)^2 + 12
\mu_2^\prime \mu^2 -6\mu^4]t^4/4! + \cdots
\end{multline*}](img59.gif)
![]() .
.
![]() are independent and
are independent and ![]() has a
has a
![]() distribution
then
distribution
then
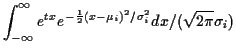
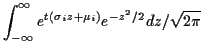
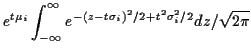
![]() are independent
are independent
![]() rvs. Then we have defined
rvs. Then we have defined
![]() to have a
to have a ![]() distribution. It is easy to check
distribution. It is easy to check ![]() has density
has density
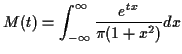
![]() is
is
![]() to the
real numbers.
to the
real numbers.
![]() and any real numbers
and any real numbers ![]() and
and ![]() are to be complex numbers then so
must
be
are to be complex numbers then so
must
be ![]() .
.
![]() with
with ![]() and
and ![]() real by
another such number, say
real by
another such number, say ![]() then the usual rules of arithmetic
(associative,
commutative and distributive laws) require
then the usual rules of arithmetic
(associative,
commutative and distributive laws) require
![]() .
.
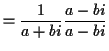
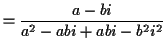
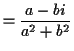
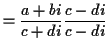
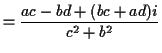
![]() we know
we know
![]() so
our insistence on the usual rules working means
so
our insistence on the usual rules working means
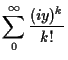
![]() with the
corresponding point
with the
corresponding point ![]() in the plane. Picture the complex numbers
as forming a plane.
in the plane. Picture the complex numbers
as forming a plane.
![]() and comparing this with our formula for the
exponential we see we can write
and comparing this with our formula for the
exponential we see we can write
![]() ,
,
![]() .
.
![]() is
is
![]() is
is
![]() .
.
![]() and
and
![]() .
.
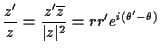
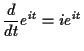
![]() is
differentiable then
is
differentiable then ![]() is analytic (has power series expansion).
is analytic (has power series expansion).
![]() is
is
![]() to
to ![]() or
or ![]() by inversion.
See homework for basic inversion formula:
by inversion.
See homework for basic inversion formula:
![]() is a random variable taking only integer values then
for each integer
is a random variable taking only integer values then
for each integer ![]()
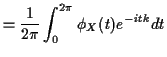
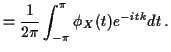
![]() has a continuous bounded density
has a continuous bounded density ![]() . Define
. Define
![$\displaystyle \frac{1}{2\pi} \int_{-\pi}^{\pi} \phi_{[nX]}(t)$](img174.gif)
![$\displaystyle n P(k/n \le X < (k+1)/n) =\frac{1}{2\pi}
\int_{-n\pi}^{n\pi} \phi_{[nX]}(u/n)e^{iuk/n} du \, .
$](img177.gif)
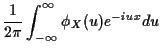
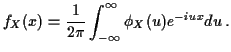
![]() .
.
![]() using a
complex contour integral:
using a
complex contour integral:
![]() and
and ![]() are two
points in the complex plane and
are two
points in the complex plane and ![]() a path between these two points we
can define the path integral
a path between these two points we
can define the path integral
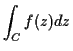
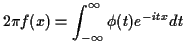
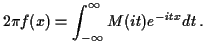
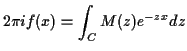
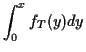
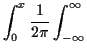
![$\displaystyle \phi(t) = \left[\frac{1}{\prod(1-2it\lambda_j)}\right]^{1/2}
$](img208.gif)
![$\displaystyle \phi(t) =
\left[\frac{\prod(1+2it\lambda_j)}{\prod(1+4t^2\lambda_j^2)}\right]^{1/2}
\, .
$](img209.gif)
![$\displaystyle \phi(t) = \left[\frac{\prod r_j e^{i\sum\theta_j}}{\prod
r_j^2}\right]^{1/2}
$](img214.gif)
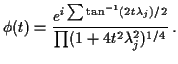
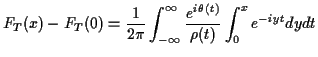
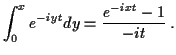
![]() are iid with mean 0 and variance 1 and
are iid with mean 0 and variance 1 and
![]() then with
then with ![]() denoting the characteristic function of
a single
denoting the characteristic function of
a single ![]() we have
we have
![$\displaystyle \approx \left[\phi(0) +\frac{t\phi^\prime(0)}{\sqrt{n}} + \frac{t^2\phi^{\prime\prime}(0)}{2n}+ o(n^{-1})\right]^n \, .$](img224.gif)
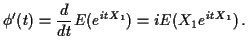
![$\displaystyle = \frac{1}{2\pi } \int_{-\infty}^\infty e^{-itx} [\phi(tn^{-1/2})]^n dt$](img233.gif)
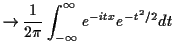
![]() to have a bounded continuous density. The central
limit theorem itself is a statement about cdfs not densities and is
to have a bounded continuous density. The central
limit theorem itself is a statement about cdfs not densities and is
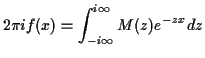
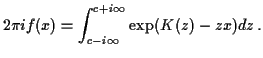
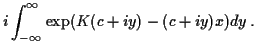
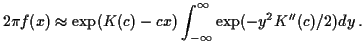
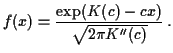
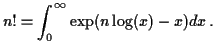
![$\displaystyle n! \approx \int_0^\infty \exp[n\log(n) - n -
(x-n)^2/(2n)] dx \, .
$](img264.gif)
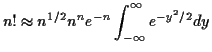
![]() not near
not near ![]() is negligible.
is negligible.