STAT 801
Problems: Assignment 2
Postscript version of these questions
- 1.
- Suppose X and Y have joint density f(x,y). Prove from the
definition of density that the density of X is
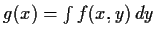 .
.
- 2.
- Suppose X is Poisson(
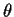 ). After observing X a coin landing
Heads with probability p is tossed X times. Let Y be the number of
Heads and Z be the number of Tails. Find the joint and marginal distributions
of Y and Z.
). After observing X a coin landing
Heads with probability p is tossed X times. Let Y be the number of
Heads and Z be the number of Tails. Find the joint and marginal distributions
of Y and Z.
- 3.
- Let p1 be the bivariate normal density with mean 0,
unit variances and correlation
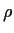 and let p2 be the standard
bivariate normal density. Let
p= (p1+p2)/2.
and let p2 be the standard
bivariate normal density. Let
p= (p1+p2)/2.
- (a)
- Show that p has normal margins but is not bivariate normal.
- (b)
- Generalize the construction to show that there rv's X and Y
such that X and Y are each standard normal, X and Y are
uncorrelated but X and Y are not independent.
- 4.
- Warning: This is probably hard. Don't waste too much time on
it. Suppose X and Y are independent
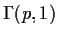 and
and
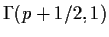 random variables. Show that
Z=2(XY)1/2 is a
random variables. Show that
Z=2(XY)1/2 is a
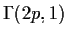 random variable.
random variable.
- 5.
- Suppose X and Y are independent with
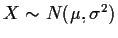 and
and
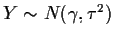 .
Let Z=X+Y.
Find the distribution of Z given X and that of X given Z.
.
Let Z=X+Y.
Find the distribution of Z given X and that of X given Z.
Richard Lockhart
1998-08-27