- (a)
- Find complete and sufficient statistics.
- (b)
- Find UMVUE's of
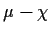 and
and
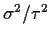 .
.
- (c)
- Now suppose you know that
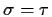 .
Find UMVUE's of
.
Find UMVUE's of
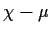 and of
and of
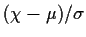 .
(You have already found
the UMVUE for
.
(You have already found
the UMVUE for 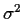 .)
.)
- (d)
- Now suppose
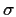 and
and 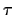 are unknown but that you
know that
are unknown but that you
know that
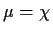 .
Prove there is no UMVUE for
.
Prove there is no UMVUE for 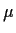 .
(Hint: Find the UMVUE if you knew
.
(Hint: Find the UMVUE if you knew
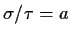 with a known.
Use the fact that the solution depends on a to finish the proof.)
with a known.
Use the fact that the solution depends on a to finish the proof.)
- (e)
- Why doesn't the Lehmann-Scheffé theorem apply?
for
- (a)
- Find the MLE's for
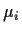 and
and 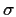 .
.
- (b)
- Find the expectations and variances of these estimators.
- (a)
- Find the joint density of the Ti.
- (b)
- Find the best estimate of
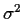 of the form
of the form
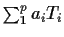 in the sense of mean squared error.
in the sense of mean squared error.
- (c)
- Do the same under the condition that the estimator must be unbiased.
- (d)
- If only
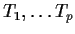 are observed what is the MLE of
are observed what is the MLE of 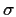 ?
?
- (e)
- Find the UMVUE of
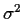 for the usual one-way layout model,
that is, the model of the last two questions.
for the usual one-way layout model,
that is, the model of the last two questions.
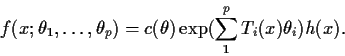
- (a)
- Find minimal sufficient statistics.
- (b)
- If
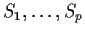 are the minimal sufficient statistics show
that setting
are the minimal sufficient statistics show
that setting
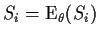 and solving gives the
likelihood equations. (Note the connection to the method of moments.)
and solving gives the
likelihood equations. (Note the connection to the method of moments.)
where
- (a)
- Find the log-likelihood, the score function and the Fisher information.
- (b)
- For the data set in
 /teaching/courses/801/data1 fit the
model and produce a contour plot of the log-likelihood surface, the profile
likelihood for
/teaching/courses/801/data1 fit the
model and produce a contour plot of the log-likelihood surface, the profile
likelihood for 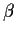 and an approximate 95% confidence interval for
and an approximate 95% confidence interval for
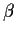 .
.
- (a)
- Compute the mean and variance covariance matrix of the vector you
get by writing out all the Xij as a vector.
- (b)
- Suppose that M is a matrix of the form aI+b11t where
I is a
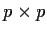 identity and 1 denotes a column vector of p ones.
Show that M-1 is of the form cI+d11t and find c and d.
In what follows you may use the fact that the determinant of M is
ap-1(a+pb).
identity and 1 denotes a column vector of p ones.
Show that M-1 is of the form cI+d11t and find c and d.
In what follows you may use the fact that the determinant of M is
ap-1(a+pb).
- (c)
- Write down the likelihood.
- (d)
- Find minimal sufficient statistics.
- (e)
- Are they complete?
- (f)
- Data sets like this are usually analyzed based on the fixed effects ANOVA
table. Use the formulas for expected mean squares in this table to develop
``method of moments'' estimates of the three parameters. (Because the data are not
iid this is not going to be exactly the same technique as the examples in class.)
- (g)
- Can you find the MLE's?
- (a)
- Find the likelihood equations for estimating
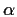 and
and 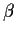 .
.
- (b)
- Find the Fisher information matrix.
- (c)
- Define the parameter LD50 as the value of d for which h(d)= 1/2;
express LD50 as a function of
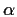 and
and 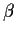 .
.
- (d)
- Use a Taylor expansion to find large sample confidence limits for LD50.
- (e)
- At each of the doses -3.204, -2.903, 2.602, -2.301 and -2.000 a sample
of 40 mice were exposed to antipneumonococcus serum. The numbers surviving
were 7, 18, 32, 35, and 38 respectively. Get numerical values for the theory
above. You can use glm or get preliminary estimates based on linear
regression of the MLE of h(di) against dose.
In the following question the digamma function
- (a)
- For
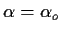 known find the mle for
known find the mle for 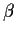 .
.
- (b)
- When both
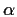 and
and 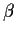 are unknown what equation must be
solved to find
are unknown what equation must be
solved to find
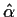 ,
the mle of
,
the mle of 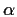 ?
?
- (c)
- Evaluate the Fisher information matrix.
- (d)
- A sample of size 20 is in the file
Use this data in the following questions. First take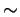 /teaching/801/gamma.
/teaching/801/gamma.
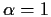 and find
the mle of
and find
the mle of 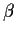 subject to this restriction.
subject to this restriction.
- (e)
- Now use
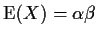 and
and
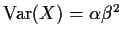 to
get method of moments estimates
to
get method of moments estimates
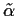 and
and
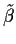 for
the parameters. (This was done in class so I just mean get numbers.)
for
the parameters. (This was done in class so I just mean get numbers.)
- (f)
- Do two steps of Newton Raphson to get MLEs.
- (g)
- Use Fisher's scoring idea, which is to replace the second derivative
in Newton Raphson with the Fisher information (and then not change it
as you run the iteration), to redo the previous question.
- (h)
- Compute standard errors for the MLEs and compare the difference
between the estimates in the previous 2 questions to the SEs.
- (i)
- Do a likelihood ratio test of
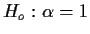 .
.