Reading for Today's Lecture: Chapter 1 of Casella and Berger.
Goals of Today's Lecture:
Today's notes
Course outline:
Standard view of scientific inference has a set of theories which make predictions about the outcomes of an experiment:
| Theory | Prediction |
| A | 1 |
| B | 2 |
| C | 3 |
If we conduct the experiment and see outcome 2 we infer that Theory B is correct (or at least that A and C are wrong).
Add Randomness
| Theory | Prediction |
| A | Usually 1 sometimes 2 never 3 |
| B | Usually 2 sometimes 1 never 3 |
| C | Usually 3 sometimes 1 never 2 |
Now if we actually see outcome 2 we infer that Theory B is probably correct, that Theory A is probably not correct and that Theory C is wrong.
Probability Theory is concerned with constructing the table just given: computing the likely outcomes of experiments.
Statistics is concerned with the inverse process of using the table to draw inferences from the outcome of the experiment. How should we do it and how wrong are our inferences likely to be?
A Probability Space (sometimes called a Sample Space) is an ordered
triple
![]() .
The idea is that
.
The idea is that ![]() is the set of possible
outcomes of a random experiment,
is the set of possible
outcomes of a random experiment, ![]() is the set of those events, or subsets
of
is the set of those events, or subsets
of ![]() whose probability is defined and P is the rule for computing probabilities.
Formally:
whose probability is defined and P is the rule for computing probabilities.
Formally:
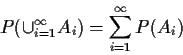
These axioms guarantee that as we compute probabilities by the usual rules, including approximation of an event by a sequence of others we don't get caught in any logical contradictions.
A vector valued random variable is a function X whose domain is ![]() and
whose range is in some p dimensional Euclidean space, Rp with the property that
the events whose probabilities we would like to calculate from their
definition in terms of X are in
and
whose range is in some p dimensional Euclidean space, Rp with the property that
the events whose probabilities we would like to calculate from their
definition in terms of X are in ![]() .
We will write
.
We will write
![]() .
We
will want to make sense of
.
We
will want to make sense of
Now for formal definitions:
The Borel ![]() -field in Rp is the smallest
-field in Rp is the smallest ![]() -field in Rp
containing every open ball.
-field in Rp
containing every open ball.
Every common set is a Borel set, that is, in the Borel ![]() -field
-field
An Rp valued random variable is a map
![]() such that
when A is Borel then
such that
when A is Borel then
![]() .
.
Fact: this is equivalent to
Jargon and notation: we write ![]() for
for
![]() and define the distribution of X to be the map
and define the distribution of X to be the map
The Cumulative Distribution Function (or CDF) of X is the function FX on Rp
defined by
Properties of FX (or just F when there's only one cdf under consideration):
The distribution of a random variable X is discrete
(we also call the random variable discrete) if there
is a countable set
![]() such that
such that
The distribution of a random variable X is absolutely continuous
if there is a function f such that
Example: X is exponential.
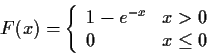

General Problem: Start with assumptions about the density or cdf of a random
vector
![]() .
Define
.
Define
![]() to be some function
of X (usually some statistic of interest). How can we compute the distribution
or cdf or density of Y?
to be some function
of X (usually some statistic of interest). How can we compute the distribution
or cdf or density of Y?
Univariate Techniques
Method 1: compute the cdf by integration and differentiate to find fY.
Example:
![]() and
and ![]() .
Then
.
Then
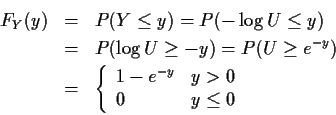
Example:
![]() ,
i.e.
,
i.e.
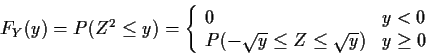
![\begin{displaymath}f_Y(y) = \left\{ \begin{array}{ll}
0 & y < 0
\\
\frac{d}{dy...
...\right] & y > 0
\\
\mbox{undefined} & y=0
\end{array}\right.
\end{displaymath}](img52.gif)
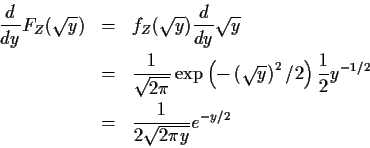
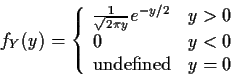
We will find indicator notation useful:
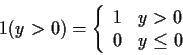
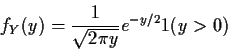
Notice: I never evaluated FY before differentiating it. In fact
FY and FZ are integrals I can't do but I can differentiate then anyway.
You should remember the fundamental theorem of calculus: