Reading for Today's Lecture:
Goals of Today's Lecture:
Review of end of last time
Proof: Reduces to ![]() and
and ![]() .
.
Step 1: Define
![\begin{align*}f_Y(y) =& (2\pi)^{-n/2} \exp[-y^t\Sigma^{-1}y/2]/\vert\det M\vert
...
...^{-(n-1)/2}\exp[-{\bf y}_2^t Q^{-1} {\bf y}_2/2]}{\vert\det M\vert}
\end{align*}](img11.gif)
Notice that this is a factorization into a function of y1 times a
function of
![]() .
Thus
.
Thus
![]() is independent of
is independent of
![]() .
Since sZ2 is a function of
.
Since sZ2 is a function of
![]() we see that
we see that
![]() and
sZ2 are independent (remember that
and
sZ2 are independent (remember that
![]() ).
).
Furthermore the density of Y1 is a multiple of the function of y1 in
the factorization above. But the factor in question is the standard normal
density so
![]() .
.
We have now done the first 2 parts of the theorem. The third part is
a homework exercise but I will outline the derivation of the ![]() density.
density.
Suppose that
![]() are independent N(0,1). We define the
are independent N(0,1). We define the
![]() distribution to be that of
distribution to be that of
![]() .
Define angles
.
Define angles
![]() by
by
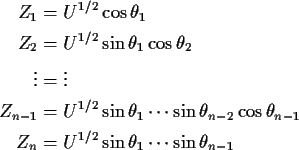
(These are spherical co-ordinates in n dimensions. The ![]() values run
from 0 to
values run
from 0 to ![]() except for the last
except for the last ![]() whose values run from 0 to
whose values run from 0 to ![]() .)
Then note the following derivative formulas
.)
Then note the following derivative formulas

![\begin{displaymath}\left[\begin{array}{ccc}
U^{-1/2} \cos\theta_1 /2
&
-U^{1/2} ...
...theta_2
&
U^{1/2} \sin\theta_1\cos\theta_2
\end{array}\right]
\end{displaymath}](img29.gif)
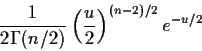
Finally the fourth part of the theorem is a consequence of the
first 3 parts of the theorem and the definition of the ![]() distribution, namely, that
distribution, namely, that
![]() if it has the same distribution
as
if it has the same distribution
as
However, I now derive the density of T in this definition:

I can differentiate this with respect to t by
simply differentiating the inner integral:
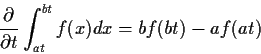
![\begin{displaymath}\frac{d}{dt} P(T \le t) =
\int_0^\infty f_U(u) \sqrt{u/\nu}\frac{\exp[-t^2u/(2\nu)]}{\sqrt{2\pi}} du
\, .
\end{displaymath}](img50.gif)

![\begin{displaymath}f_T(t) = \int_0^\infty \frac{1}{2\sqrt{\pi\nu}\Gamma(\nu/2)}
(u/2)^{(\nu-1)/2} \exp[-u(1+t^2/\nu)/2] \, du \, .
\end{displaymath}](img52.gif)

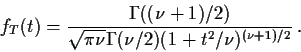
In elementary courses we give two definitions of expected values:
Def'n If X has density f then
Def'n: If X has discrete density f then

Now if Y=g(X) for smooth g then
In general, there are random variables which are neither absolutely continuous nor discrete. Here's how probabilists define E in general.
Def'n: A random variable X is simple if we can write

Def'n: For a simple rv X we define
For positive random variables which are not simple we extend our definition by approximation:
Def'n: If ![]() then
then
Def'n: We call X integrable if
Facts: E is a linear, monotone, positive operator:
Major technical theorems:
Monotone Convergence: If
![]() and
and
![]() (which has to exist) then
(which has to exist) then
Dominated Convergence: If
![]() and there
is a random variable X such that
and there
is a random variable X such that ![]() (technical
details of this convergence later in the course) and
a random variable Y such that
(technical
details of this convergence later in the course) and
a random variable Y such that ![]() with
with
![]() then
then
Fatou's Lemma: If ![]() then
then
Theorem: With this definition of E if X has density
f(x) (even in Rp say) and Y=g(X) then
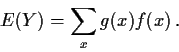
This works for instance even if X has a density but Y doesn't.
Def'n: The
![]() moment (about the origin) of a real
random variable X is
moment (about the origin) of a real
random variable X is
![]() (provided it exists).
We generally use
(provided it exists).
We generally use
![]() for E(X). The
for E(X). The
![]() central moment is
central moment is
Def'n: For an Rp valued random vector X we define
![]() to be the vector whose
to be the vector whose
![]() entry is E(Xi)
(provided all entries exist).
entry is E(Xi)
(provided all entries exist).
Def'n: The (
![]() )
variance covariance matrix of X is
)
variance covariance matrix of X is
Moments and probabilities of rare events are closely connected as will
be seen in a number of important probability theorems. Here is one
version of Markov's inequality (one case is Chebyshev's inequality):
![\begin{align*}P(\vert X-\mu\vert \ge t ) &= E[1(\vert X-\mu\vert \ge t)]
\\
&\...
...-\mu\vert \ge t)\right]
\\
& \le \frac{E[\vert X-\mu\vert^r]}{t^r}
\end{align*}](img93.gif)
The intuition is that if moments are small then large deviations from
average are unlikely.
Example moments: If Z is standard normal then

and (integrating by parts)

so that


If now
![]() ,
that is,
,
that is,
![]() ,
then
,
then
![]() and
and
Theorem: If
![]() are independent and each Xi is
integrable then
are independent and each Xi is
integrable then
![]() is integrable and
is integrable and
Proof: Suppose each Xi is simple:
![]() where the xij are the possible values of Xi. Then
where the xij are the possible values of Xi. Then
![\begin{align*}E(X_1\cdots X_p) & = \sum_{j_1\ldots j_p} x_{1j_1}\cdots x_{pj_p} ...
...ft[\sum_{j_p} x_{pj_p} P(X_p = x_{pj_p})\right]
\\
&= \prod E(X_i)
\end{align*}](img111.gif)
For general Xi>0 we create a sequence of simple approximations
by rounding Xi down to the nearest multiple of 2-n (to
a maximum of n) and applying the case just done and the monotone
convergence theorem. The general case uses the fact that
we can write each Xi as the difference of its positive and negative
parts:
Def'n: The moment generating function of a real valued X is
Def'n: The moment generating function of ![]() is
is
The mgf has the following formal connection to moments:
![\begin{align*}M_X(t) & = \sum_{k=0}^\infty E[(tX)^k]/k!
\\
= \sum_{k=0}^\infty \mu_k^\prime t^k/k!
\end{align*}](img115.gif)
It is thus sometimes possible to find the power series expansion of
MX and read off the moments of X from the coefficients of the
powers tk/k!.
Theorem: If M is finite for all
![]() for some
for some
![]() then
then
The proof, and many other facts about mgfs, rely on techniques of complex variables.