Reading for Today's Lecture:
Goals of Today's Lecture:
Review of end of last time
I defined independent events and then independent random variables:
Definition: Events Ai,
![]() are
independent if
are
independent if
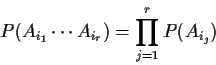
Definition: Random variables
![]() are
independent if
are
independent if
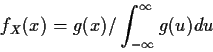
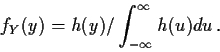
New material
Proof:
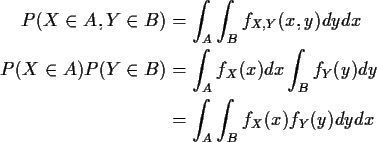
![\begin{displaymath}\int_A\int_B [ f_{X,Y}(x,y) - f_X(x)f_Y(y) ]dydx = 0
\end{displaymath}](img16.gif)
![\begin{align*}P(X \in A, Y \in B) & = P(X\in A)P(Y \in B)
\\
&= \int_Af_X(x)dx \int_B f_Y(y) dy
\\
&= \int_A\int_B f_X(x)f_Y(y) ]dydx
\end{align*}](img17.gif)



Def'n:
P(A|B) = P(AB)/P(B) provided
![]() .
.
Def'n: For discrete random variables X and Y the conditional
probability mass function of Y given X is
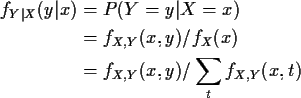
For absolutely continuous X the problem is that
P(X=x) = 0 for all
x so how can we define P(A| X=x) or
fY|X(y|x)?
The solution is to take a limit
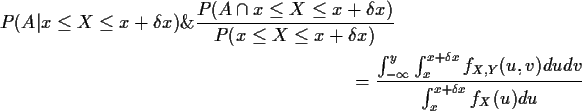
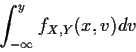

Def'n:
![]() iff
iff

Def'n:
![]() iff
iff
![]() (a column vector for later use) with the
Zi independent and each
(a column vector for later use) with the
Zi independent and each
![]() .
.
In this case according to our theorem

where the superscript t denotes matrix transpose.
Def'n: ![]() has a multivariate normal distribution if it
has the same distribution as
has a multivariate normal distribution if it
has the same distribution as ![]() for some
for some
![]() ,
some
,
some
![]() matrix of constants A and
matrix of constants A and
![]() .
.
If the matrix A is singular then X will not have a density. If A is
invertible then we can derive the multivariate normal density
by the change of variables formula:

For which vectors ![]() and matrices
and matrices ![]() is this a density?
Any
is this a density?
Any ![]() will work but if
will work but if ![]() then
then

where y=At x. The inequality is strict except for y=0 which
is equivalent to x=0. Thus ![]() is a positive definite symmetric
matrix. Conversely, if
is a positive definite symmetric
matrix. Conversely, if ![]() is a positive definite symmetric matrix
then there is a square invertible matrix A such that
is a positive definite symmetric matrix
then there is a square invertible matrix A such that
![]() so that
there is a
so that
there is a
![]() distribution. (The matrix A can be found
via the Cholesky decomposition, for example.)
distribution. (The matrix A can be found
via the Cholesky decomposition, for example.)
More generally we say that X has a multivariate normal distribution
if it has the same distribution as ![]() where now we remove the
restriction that A be non-singular. When A is singular X will not
have a density because there will exist an a such that
where now we remove the
restriction that A be non-singular. When A is singular X will not
have a density because there will exist an a such that
![]() ,
that is, so that X is confined to a hyperplane. It is still
true, however, that the distribution of X depends only on the matrix
,
that is, so that X is confined to a hyperplane. It is still
true, however, that the distribution of X depends only on the matrix
![]() in the sense that if
AAt = BBt then
in the sense that if
AAt = BBt then ![]() and
and
![]() have the same distribution.
have the same distribution.
Properties of the MVN distribution
1: All margins are multivariate normal: if
![\begin{displaymath}X = \left[\begin{array}{c} X_1\\ X_2\end{array} \right]
\end{displaymath}](img64.gif)
![\begin{displaymath}\mu = \left[\begin{array}{c} \mu_1\\ \mu_2\end{array} \right]
\end{displaymath}](img65.gif)
![\begin{displaymath}\Sigma = \left[\begin{array}{cc} \Sigma_{11} & \Sigma_{12}
\\
\Sigma_{21} & \Sigma_{22} \end{array} \right]
\end{displaymath}](img66.gif)
2: All conditionals are normal: the conditional distribution of X1
given X2=x2 is
![]()
3:
![]() .
That is, an affine
transformation of a Multivariate Normal is normal.
.
That is, an affine
transformation of a Multivariate Normal is normal.
Proof: Let
![]() .
Then
.
Then
![]() are
independent N(0,1) so
are
independent N(0,1) so
![]() is multivariate
standard normal. Note that
is multivariate
standard normal. Note that
![]() and
and
![]() Thus
Thus
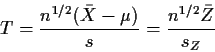
Thus we need only give a proof in the special case ![]() and
and ![]() .
.
Step 1: Define
![\begin{displaymath}Y =\left[\begin{array}{cccc}
\frac{1}{\sqrt{n}} &
\frac{1}{\s...
...in{array}{c}
Z_1 \\
Z_2 \\
\vdots
\\
Z_n
\end{array}\right]
\end{displaymath}](img88.gif)
![\begin{align*}MM^t & = \left[\begin{array}{c\vert cccc}
1 & 0 & 0 & \cdots & 0 \...
...egin{array}{c\vert c}
1 & 0
\\
\hline
\\
0 & Q
\end{array}\right]
\end{align*}](img90.gif)
Now it is easy to solve for Z from Y because
Zi = n-1/2Y1+Yi+1
for
![]() .
To get Zn we use the identity
.
To get Zn we use the identity
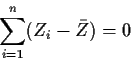
![\begin{displaymath}\Sigma^{-1} \equiv (MM^t)^{-1} =
\left[\begin{array}{c\vert c}
1 & 0
\\
\hline
\\
0 & Q^{-1}
\end{array}\right]
\end{displaymath}](img94.gif)
Now we use the change of variables formula to compute the density
of Y. It is helpful to let ![]() denote the n-1 vector whose
entries are
denote the n-1 vector whose
entries are
![]() .
Note that
.
Note that
![\begin{align*}f_Y(y) =& (2\pi)^{-n/2} \exp[-y^t\Sigma^{-1}y/2]/\vert\det M\vert
...
...^{-(n-1)/2}\exp[-{\bf y}_2^t Q^{-1} {\bf y_2}/2]}{\vert\det M\vert}
\end{align*}](img98.gif)
Notice that this is a factorization into a function of y1 times a
function of
![]() .
Thus
.
Thus
![]() is independent of
is independent of
![]() .
Since sZ2 is a function of
.
Since sZ2 is a function of
![]() we see that
we see that
![]() and
sZ2 are independent.
and
sZ2 are independent.
Furthermore the density of Y1 is a multiple of the function of y1 in
the factorization above. But the factor in question is the standard normal
density so
![]() .
.
We have now done the first 2 parts of the theorem. The third part is
a homework exercise but I will outline the derivation of the ![]() density.
density.
Suppose that
![]() are independent N(0,1). We define the
are independent N(0,1). We define the
![]() distribution to be that of
distribution to be that of
![]() .
Define angles
.
Define angles
![]() by
by

(These are spherical co-ordinates in n dimensions. The ![]() values run
from 0 to
values run
from 0 to ![]() except for the last
except for the last ![]() whose values run from 0 to
whose values run from 0 to ![]() .)
Then note the following derivative formulas
.)
Then note the following derivative formulas
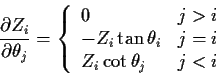
![\begin{displaymath}\left[\begin{array}{ccc}
U^{-1/2} \cos\theta_1 /2
&
-U^{1/2} ...
...theta_2
&
U^{1/2} \sin\theta_1\cos\theta_2
\end{array}\right]
\end{displaymath}](img113.gif)

Finally the fourth part of the theorem is a consequence of the
first 3 parts of the theorem and the definition of the ![]() distribution, namely, that
distribution, namely, that
![]() if it has the same distribution
as
if it has the same distribution
as
However, I now derive the density of T in this definition:

I can differentiate this with respect to t by
simply differentiating the inner integral:

![\begin{displaymath}\frac{d}{dt} P(T \le t) =
\int_0^\infty f_U(u) \sqrt{u/\nu}\frac{\exp[-t^2u/(2\nu)]}{\sqrt{2\pi}} du
\, .
\end{displaymath}](img134.gif)

![\begin{displaymath}f_T(t) = \int_0^\infty \frac{1}{2\sqrt{\pi\nu}\Gamma(\nu/2)}
(u/2)^{(\nu-1)/2} \exp[-u(1+t^2/\nu)/2] \, du \, .
\end{displaymath}](img136.gif)

