Postscript version of these notes

STAT 801 Lecture 23

Reading for Today's Lecture:

Goals of Today's Lecture:

• Introduce confidence sets.

• Describe relation of tests to confidence intervals.

• Describe the use of pivots to make confidence sets.

• Introduce decision theory.

Today's notes

Confidence Sets

A level $\beta$ confidence set for a parameter $\phi(\theta)$ is a random subset C, of the set of possible values of $\phi$ such that for each $\theta$ we have

$$P_\theta(\phi(\theta) \in C) \ge \beta$$

Confidence sets are very closely connected with hypothesis tests:

Suppose C is a level $\beta=1-\alpha$ confidence set for $\phi$. To test $\phi=\phi_0$ we consider the test which rejects if $\phi\not\in C$. This test has level $\alpha$. Conversely, suppose that for each $\phi_0$ we have available a level $\alpha$ test of $\phi=\phi_0$ who rejection region is say $R_{\phi_0}$. Then if we define $C=\{\phi_0: \phi=\phi_0 \mbox{ is not rejected}\}$ we get a level $1-\alpha$ confidence for $\phi$. The usual t test gives rise in this way to the usual t confidence intervals

$$\bar{X} \pm t_{n-1,\alpha/2} \frac{s}{\sqrt{n}}$$

which you know well.

Confidence sets from Pivots

Definition: A pivot (or pivotal quantity) is a function $g(\theta,X)$ whose distribution is the same for all $\theta$. (As usual the $\theta$ in the pivot is the same $\theta$ as the one being used to calculate the distribution of $g(\theta,X)$.

Pivots can be used to generate confidence sets as follows. Pick a set A in the space of possible values for g. Let $\beta=P_\theta(g(\theta,X) \in A)$; since g is pivotal $\beta$ is the same for all $\theta$. Now given a data set X solve the relation

$$g(\theta,X) \in A$$

to get

$$\theta \in C(X,A) \, .$$

Example: The quantity

$$(n-1) s^2/\sigma^2$$

is a pivot in the $N(\mu,\sigma^2)$ model. It has a $\chi_{n-1}^2$ distribution. Given $\beta=1-\alpha$ consider the two points $\chi_{n-1,1-\alpha/2}^2$ and $\chi_{n-1,\alpha/2}^2$. Then

$$P(\chi_{n-1,1-\alpha/2}^2 \le (n-1) s^2/\sigma^2 \le \chi_{n-1,\alpha/2}^2) = \beta$$

for all $\mu,\sigma$. We can solve this relation to get

$$P( \frac{(n-1)^{1/2} s}{ \chi_{n-1,\alpha/2}} \le \sigma \le \frac{(n-1)^{1/2} s}{ \chi_{n-1,1-\alpha/2}}) = \beta$$

so that the interval from $(n-1)^{1/2} s/\chi_{n-1,\alpha/2}$ to $(n-1)^{1/2} s/\chi_{n-1,1-\alpha/2}$ is a level $1-\alpha$ confidence interval.

In the same model we also have

$$P(\chi_{n-1,1-\alpha}^2 \le (n-1) s^2/\sigma^2 ) = \beta$$

which can be solved to get

$$P(\sigma \le \frac{(n-1)^{1/2} s}{ \chi_{n-1,1-\alpha/2}}) = \beta$$

This gives a level $1-\alpha$ interval $(0,(n-1)^{1/2} s/\chi_{n-1,1-\alpha})$. The right hand end of this interval is usually called a confidence upper bound.

In general the interval from $(n-1)^{1/2} s/\chi_{n-1,\alpha_1}$ to $(n-1)^{1/2} s/\chi_{n-1,1-\alpha_2}$ has level $\beta = 1 -\alpha_1-\alpha_2$. For a fixed value of $\beta$ we can minimize the length of the resulting interval numerically. This sort of optimization is rarely used. See your homework for an example of the method.

Decision Theory and Bayesian Methods

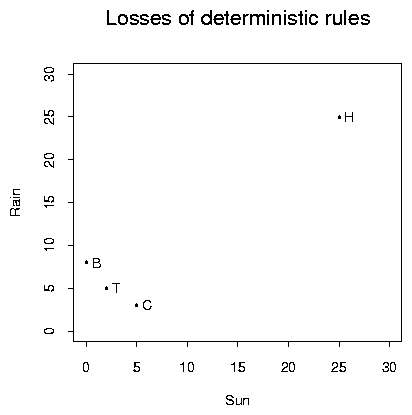
Example: I get up in the morning and must decide between 4 modes of transportation to work:

• B = Ride my bike.

• C = Take the car.

• T = Use public transit.

• H = Stay home.

Costs to me depend on the weather that day: R = Rain or S = Sun.

Ingredients of a Decision Problem: No data case.

• Decision space $D=\{B,C,T,H\}$ of possible actions I might take.

• Parameter space $\Theta = \{R,S\}$ of possible ``states of nature''.

• Loss function $L=L(d,\theta)$ which is the loss I incur if I do d and $\theta$ is the true state of nature.

In the example we might use the following table for L:

	C	B	T	H
R	3	8	5	25
S	5	0	2	25

Notice that if it rains I will be glad if I drove. If it is sunny I will be glad if I rode my bike. In any case staying at home is expensive.

In general we study this problem by comparing various functions of $\theta$. In this problem a function of $\theta$ has only two values, one for rain and one for sun and we can plot any such function as a point in the plane. We do so to indicate the geometry of the problem before stating the general theory.

Statistical Decision Theory

Statistical problems have another ingredient, the data. We observe X a random variable taking values in say $\cal X$. We may make our decision d depend on X. A decision rule is a function $\delta(X)$ from $\cal X$ to D. We will want $L(\delta(X),\theta)$ to be small for all $\theta$. Since X is random we quantify this by averaging over X and compare procedures $\delta$ in terms of the risk function

$$R_\delta(\theta) = E_\theta(L(\delta(X),\theta))$$

To compare two procedures we must compare two functions of $\theta$ and pick ``the smaller one''. But typically the two functions will cross each other and there won't be a unique `smaller one'.

Example: In estimation theory to estimate a real parameter $\theta$ we used $D=\Theta$,

$$L(d,\theta) = (d-\theta)^2$$

and find that the risk of an estimator $\hat\theta(X)$ is

$$R_{\hat\theta}(\theta) = E[(\hat\theta-\theta)^2]$$

which is just the Mean Squared Error of $\hat\theta$. We have already seen that there is no unique best estimator in the sense of MSE. How do we compare risk functions in general?

• Minimax methods choose $\delta$ to minimize the worst case risk:
  
  $$\sup\{R_\delta(\theta);\theta\in\Theta)\}.$$
  
  
  We call $\delta^*$ minimax if
  
  $$\sup_\theta R_{\delta^*}(\theta) = \inf_\delta \sup_\theta R_\delta(\theta)$$
  
  
  Usually the suprema and infima are achieved and we write $\max$ for $\sup$ and $\min$ for $\inf$. This is the source of ``minimax''.

• Bayes methods choose $\delta$ to minimize an average
  
  $$r_\pi(\delta) = \int R_\delta(\theta) \pi(\theta) d\theta$$
  
  
  for a suitable density $\pi$. We call $\pi$ a prior density and r the Bayes risk of $\delta$ for the prior $\pi$.

Example: For my transportation problem there is no data so the only possible (non-randomized) decisions are the four possible actions B,C,T,H. For B and T the worst case is rain. For the other two actions Rain and Sun are equivalent. We have the following table:

	C	B	T	H
R	3	8	5	25
S	5	0	2	25
Maximum	5	8	5	25

The smallest maximum arises for taking my car. The minimax action is to take my car or public transit.

Now imagine each morning I toss a coin with probability $\lambda$ of getting Heads and take my car if I get Heads, otherwise taking transit. Now in the long run my average daily loss for this procedure would be $3 \lambda + 5(1-\lambda)$ when it rains and $5\lambda +2(1-\lambda)$ when it is Sunny. I will call this procedure $d_\lambda$ and add it to my graph for each value of $\lambda$. Notice that on the graph varying $\lambda$ from 0 to 1 gives a straight line running from (3,5) to (5,2). The two losses are equal when $\lambda=3/5$. For smaller $\lambda$ the worst case risk is for sun while for larger $\lambda$ the worst case risk is for rain.

On the graph below I have added the loss functions for each $d_\lambda$, (a straight line) and the set of (x,y) pairs for which $\min(x,y) = 3.8$; this is the worst case risk for $d_\lambda$ when $\lambda=3/5$.

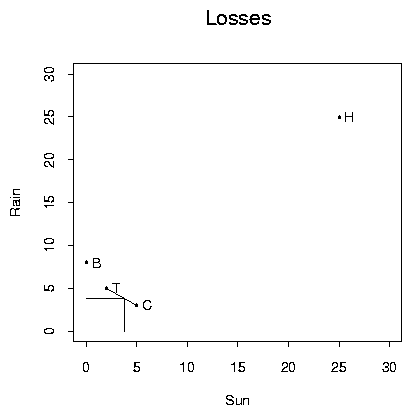
The figure then shows that d_3/5 is actually the minimax procedure when randomized procedures are permitted.

In general we might consider using a 4 sided coin where we took action B with probability $\lambda_B$, C with probability $\lambda_C$ and so on. The loss function of such a procedure is a convex combination of the losses of the four basic procedures making the set of risks achievable with the aid of randomization look like the following:

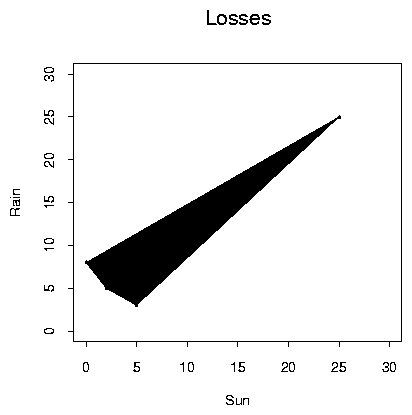
The use of randomization in general decision problems permits us to assume that the set of possible risk functions is convex. This is an important technical conclusion; it permits us to prove many of the basic results of decision theory.

Studying the graph we can see that many of the points in the picture correspond to bad decision procedures. Regardless of whether or not it rains taking my car to work has a lower loss than staying home; we call the decision to stay home inadmissible.

Definition: A decision rule $\delta$ is inadmissible if there is a rule $\delta^*$ such that

$$R_{\delta^*}(\theta) \le R_\delta(\theta)$$

for all $\theta$ and there is at least one value of $\theta$ where the inequality is strict. A rule which is not inadmissible is called admissible.

The admissible procedures have risks on the lower left of the graphs above. That is, the two lines connecting B to T and T to C are the admissible procedures.

There is a connection between Bayes procedures and admissible procedures. A prior distribution in our example problem is specified by two probabilities, $\pi_R$ and $\pi_S$ which add up to 1. If L=(L_R,L_S) is the risk function for some procedure then the Bayes risk is

$$r_\pi= \pi_R L_R + \pi_S L_S$$

Consider the set of L such that this Bayes risk is equal to some constant. On our picture this is a straight line with slope $-\pi_R/\pi_S$. Consider now three priors $\pi_1 = (0.9,0.1)$, $\pi_2 = (0.5,0.5)$ and $\pi_3= (0.1,0.9)$. For say $\pi_1$ imagine a line with slope -9 =0.9/0.1 starting on the far left of the picture and sliding right until it bumps into the convex set of possible losses in the previous picture. It does so at point B as shown in the next graph. Sliding this line to the right corresponds to making the value of $r_\pi$ larger and larger so that when it just touches the convex set we have found the Bayes procedure.

Here is a picture showing the same lines for the three priors above.

We see that the Bayes procedure for $\pi_1$ (you are pretty sure it will be sunny) is to ride your bike. If it's a toss up between R and S you take the bus. If R is very likely you take your car.

The special prior (0.6,0.4) produces the line shown here:

You can see that any point on the line connecting B to T is Bayes for this prior.

The ideas here can be used to prove the following general facts:

• Every admissible procedure is Bayes. (Proof uses the Separating Hyperplane Theorem in Functional Analysis.)

• Every Bayes procedure is admissible. (Proof: If $\delta$ is Bayes for $\pi$ but not admissible there is a $\delta^*$ such that
  
  $$R_{\delta^*}(\theta) \le R_\delta(\theta)$$
  
  
  Multiply by the prior density and integrate to deduce
  
  $$r_\pi(\delta^*) \le r_\pi(\delta)$$
  
  
  If there is a $\theta$ for which the inequality involving R is strict and if the density of $\pi$ is positive at that $\theta$ then the inequality for $r_\pi$ is strict which would contradict the hypothesis that $\delta$ is Bayes for $\pi$. Notice that this theorem actually requires the extra hypothesis about the positive density.)

• A minimax procedure is admissible. (Actually there can be several minimax procedures and the claim is that at least one of them is admissible. When the parameter space is infinite it might happen that set of possible risk functions is not closed; if not then we have to replace the notion of admissible by some notion of nearly admissible.)

• The minimax procedure has constant risk. Actually the admissible minimax procedure is Bayes for some $\pi$ and its risk is constant on the set of $\theta$ for which the prior density is positive.

Bayesian estimation

Now let's focus on the problem of estimation of a 1 dimensional parameter. Mean Squared Error corresponds to using

$$L(d,\theta) = (d-\theta)^2 \, .$$

The risk function of a procedure (estimator) $\hat\theta$ is

$$R_{\hat\theta}(\theta) =E_\theta[(\hat\theta-\theta)^2 ]$$

Now consider using a prior with density $\pi(\theta)$. The Bayes risk of $\hat\theta$ is
$$\begin{align*}r_\pi & = \int R_{\hat\theta}(\theta)\pi(\theta) d\theta \\ & = \int \int (\hat\theta(x) - \theta)^2 f(x;\theta) \pi(\theta) dx d\theta \end{align*}$$