


Postscript version of these notes
STAT 801 Lecture 24
Reading for Today's Lecture:
Goals of Today's Lecture:
- Introduce Decision Theory.
- Discuss priors, posteriors, posterior expected risk.
- Discuss admissible, minimax and Bayes procedures.
Today's notes
Decision Theory and Bayesian Methods
- Decision space is the set of possible actions I might take. We assume
that it is convex, typically by expanding a basic decision space D to
the space
of all probability distributions on D.
- Parameter space
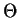 of possible ``states of nature''.
of possible ``states of nature''.
- Loss function
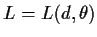 which is the loss I incur if I do d and
which is the loss I incur if I do d and
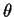 is the true state of nature.
is the true state of nature.
- We call
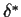 minimax if
minimax if
- A prior is a probability distribution
 on
on 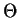 ,.
,.
- The Bayes risk of a decision
 for a prior
for a prior  is
is
if the prior has a density. For finite parameter spaces 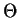 the
integral is a sum.
the
integral is a sum.
- A decision
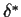 is Bayes for a prior
is Bayes for a prior  if
if
for any decision  .
.
- When the parameter space is infinite we sometimes have to consider
prior ``densities'' which are not really densities because they have
integral equal to
 .
A positive function on
.
A positive function on 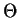 is called
a proper prior if it has a finite integral; in this case we divide through
by that integral to get a density. A positive function on
is called
a proper prior if it has a finite integral; in this case we divide through
by that integral to get a density. A positive function on 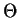 whose
integral is infinite is an improper prior density.
whose
integral is infinite is an improper prior density.
- A decision
 is inadmissible if there is
a decision
is inadmissible if there is
a decision 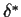 such that
such that
for all 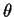 and there is at least one value of
and there is at least one value of 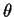 where the
inequality is strict. A decision which is not inadmissible is called
admissible.
where the
inequality is strict. A decision which is not inadmissible is called
admissible.
- Every admissible procedure is Bayes, perhaps only for an improper
prior. (Proof uses the Separating
Hyperplane Theorem in Functional Analysis.)
- Every Bayes procedure with finite Bayes risk
(for a prior which has a density
which is positive for all
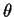 )
is admissible. (Proof: If
)
is admissible. (Proof: If  is
Bayes for
is
Bayes for  but not admissible there is a
but not admissible there is a 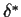 such that
such that
Multiply by the prior density and integrate to deduce
If there is a 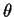 for which the inequality involving L is
strict and if the density of
for which the inequality involving L is
strict and if the density of  is positive at that
is positive at that 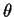 then
the inequality for
then
the inequality for  is strict which would contradict the hypothesis
that
is strict which would contradict the hypothesis
that  is Bayes for
is Bayes for  .
Notice that this theorem actually
requires the extra hypothesis about the positive density and that the
risk functions of
.
Notice that this theorem actually
requires the extra hypothesis about the positive density and that the
risk functions of  and
and 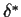 be continuous.)
be continuous.)
- A minimax procedure is admissible. (Actually there can be several
minimax procedures and the claim is that at least one of them is
admissible. When the parameter space is infinite it might happen that set
of possible risk functions is not closed; if not then we have to replace
the notion of admissible by some notion of nearly admissible.)
- The minimax procedure has constant risk. Actually the admissible
minimax procedure is Bayes for some
 and its risk is constant on
the set of
and its risk is constant on
the set of 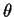 for which the prior density is positive.
for which the prior density is positive.
Statistical Decision Theory
Statistical problems have another ingredient, the data. We observe
X a random variable taking values in say  .
We may make our decision d depend on X. A
decision rule is a function
.
We may make our decision d depend on X. A
decision rule is a function  from
from  to D.
We will want
to D.
We will want
 to be small for all
to be small for all 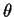 .
Since
X is random we quantify this by averaging over X and compare procedures
.
Since
X is random we quantify this by averaging over X and compare procedures
 in terms of the risk function
in terms of the risk function
To compare two procedures we must compare two functions of 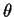 and
pick ``the smaller one''. But typically the two functions will cross each
other and there won't be a unique `smaller one'.
and
pick ``the smaller one''. But typically the two functions will cross each
other and there won't be a unique `smaller one'.
Example: In estimation theory to estimate a real parameter
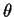 we used
we used  ,
,
and find that the risk of an estimator
 is
is
which is just the Mean Squared Error of
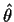 .
We have already seen that there is no unique best estimator in
the sense of MSE. How do we compare risk functions in general? We
extend minimax and bayes to risks rather than just losses.
.
We have already seen that there is no unique best estimator in
the sense of MSE. How do we compare risk functions in general? We
extend minimax and bayes to risks rather than just losses.
- Minimax methods choose
 to minimize the worst case
risk:
to minimize the worst case
risk:
We call 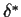 minimax if
minimax if
Usually the suprema and infima are achieved and we write  for
for 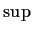 and
and  for
for 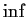 .
This is the source of ``minimax''.
.
This is the source of ``minimax''.
- Bayes methods choose
 to minimize an average
to minimize an average
for a suitable density  .
We call
.
We call  a prior density
and r the Bayes risk of
a prior density
and r the Bayes risk of  for the prior
for the prior  .
.
Definition: A decision rule  is inadmissible if there is
a rule
is inadmissible if there is
a rule 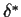 such that
such that
for all 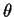 and there is at least one value of
and there is at least one value of 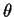 where the
inequality is strict. A rule which is not inadmissible is called admissible.
where the
inequality is strict. A rule which is not inadmissible is called admissible.
Bayesian estimation
Now let's focus on the problem of estimation of a 1 dimensional
parameter. Mean Squared Error
corresponds to using
The risk function of a procedure (estimator)
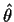 is
is
Now consider using a prior with density
 .
The
Bayes risk of
.
The
Bayes risk of
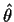 is
is

How should we choose
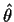 to minimize
to minimize  ? The solution
lies in recognizing that
? The solution
lies in recognizing that
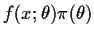 is really a joint
density
is really a joint
density
For this joint density the conditional density of X given 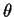 is just the model
is just the model
 .
From now on I write the model as
.
From now on I write the model as
 to emphasize this fact. We can now compute
to emphasize this fact. We can now compute  a different way by factoring the joint density a different way:
a different way by factoring the joint density a different way:
where now f(x) is the marginal density of x and
 denotes the conditional density of
denotes the conditional density of 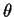 given X. We call
given X. We call
 the posterior density. It is found via
Bayes theorem (which is why this is Bayesian statistics):
the posterior density. It is found via
Bayes theorem (which is why this is Bayesian statistics):
With this notation we can write
Now we can choose
 separately for each x to minimize the
quantity in square brackets (as in the NP lemma). The quantity in
square brackets is a quadratic function of
separately for each x to minimize the
quantity in square brackets (as in the NP lemma). The quantity in
square brackets is a quadratic function of
 and can be seen
to be minimized by
and can be seen
to be minimized by
which is
and is called the posterior expected mean of 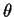 .
.
Example: Consider first the problem of estimating a normal
mean  .
Imagine, for example that
.
Imagine, for example that  is the true speed of sound.
I think this is around 330 metres per second and am pretty sure that I
am within 30 metres per second of the truth with that guess. I might
summarize my opinion by saying that I think
is the true speed of sound.
I think this is around 330 metres per second and am pretty sure that I
am within 30 metres per second of the truth with that guess. I might
summarize my opinion by saying that I think  has a normal distribution
with mean
has a normal distribution
with mean 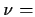 330 and standard deviation
330 and standard deviation  .
That is, I take a
prior density
.
That is, I take a
prior density  for
for  to be
.
Before I make any
measurements my best guess of
to be
.
Before I make any
measurements my best guess of  minimizes
minimizes
This quantity is minimized by the prior mean of  ,
namely,
,
namely,
Now suppose we collect 25 measurements of the speed of sound. I will
assume that the relationship between the measurements and  is that
the measurements are unbiased and that the standard deviation of the
measurement errors is
is that
the measurements are unbiased and that the standard deviation of the
measurement errors is 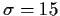 which I assume that we know. Thus the
model is that conditional on
which I assume that we know. Thus the
model is that conditional on 
 are iid
are iid
 .
The joint density of the data and
.
The joint density of the data and  is then
is then
This is a multivariate normal joint density for
 so the conditional distribution of
so the conditional distribution of 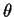 given
given
 is
normal. Standard multivariate normal formulas can be used to calculate
the conditional means and variances. Alternatively the exponent in the
joint density is of the form
is
normal. Standard multivariate normal formulas can be used to calculate
the conditional means and variances. Alternatively the exponent in the
joint density is of the form
plus terms not involving  where
where
and
This means that the conditional density of  given the data is
given the data is
 .
In other words the posterior mean of
.
In other words the posterior mean of  is
is
which is a weighted average of the prior mean  and the sample
mean
and the sample
mean 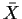 .
Notice that the weight on the data is large when n
is large or
.
Notice that the weight on the data is large when n
is large or  is small (precise measurements) and small when
is small (precise measurements) and small when
 is small (precise prior opinion).
is small (precise prior opinion).
Improper priors: When the density does not integrate
to 1 we can still follow the machinery of Bayes' formula to derive
a posterior. For instance in the
 example consider
the prior density
example consider
the prior density
 .
This ``density'' integrates
to
.
This ``density'' integrates
to  but using Bayes' theorem to compute the posterior would
give
but using Bayes' theorem to compute the posterior would
give
It is easy to see that this cancels to the limit of the case previously
done when
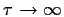 giving a
giving a
 density.
That is, the Bayes estimate of
density.
That is, the Bayes estimate of  for this improper prior is
for this improper prior is 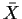 .
.
Admissibility: ayes procedures for proper priors are
admissible. It follows that for each
 and each real
and each real  the estimate
the estimate
is admissible. That this is also true for w=1, that is, that 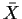 is admissible is much harder to prove.
is admissible is much harder to prove.
Minimax estimation: The risk function of 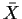 is simply
is simply
 .
That is, the risk function is constant since
it does not depend on
.
That is, the risk function is constant since
it does not depend on  .
Were
.
Were 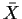 Bayes for a proper
prior this would prove that
Bayes for a proper
prior this would prove that 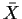 is minimax. In fact this is also
true but hard to prove.
is minimax. In fact this is also
true but hard to prove.
Example: Suppose that given p X has a Binomial(n,p)
distribution. We will give p a Beta
 prior density
prior density
The joint ``density'' of X and p is
so that the posterior density of p given X is of the form
for a suitable normalizing constant c. But this is a
Beta
 density. The mean of a Beta
density. The mean of a Beta
 distribution is
distribution is
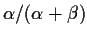 .
Thus the Bayes estimate
of p is
.
Thus the Bayes estimate
of p is
where
 is the usual mle.
Notice that this is again a weighted average of the prior mean and
the mle. Notice also that the prior is proper for
is the usual mle.
Notice that this is again a weighted average of the prior mean and
the mle. Notice also that the prior is proper for  and
and
 .
To get w=1 we take
.
To get w=1 we take
 and use the improper
prior
and use the improper
prior
Again we learn that each
 is admissible for
is admissible for
 .
Again it is true that
.
Again it is true that  is admissible but that
our theorem is not adequate to prove this fact.
is admissible but that
our theorem is not adequate to prove this fact.
The risk function of
 is
is
which is
This risk function will be constant if the coefficients of
both p2 and of p in the risk are 0. The coefficient of
p is
-w2/n +(1-w)2
so
w=n1/2/(1+n1/2). The coefficient of p is then
w2/n -2p0(1-w)2
which will vanish if 2p0=1 or p0=1/2. Working
backwards we find that to get these values for w and p0
we require
 .
Moreover the equation
.
Moreover the equation
w2/(1-w)2 = n
gives
or
 .
The minimax estimate of
p is
.
The minimax estimate of
p is
Example: Now suppose that
 are iid
are iid
 with
with  known. Consider as the improper prior for
known. Consider as the improper prior for  which is constant. The
posterior density of
which is constant. The
posterior density of  given X is then
given X is then
 .
.
For multivariate estimation it is common to extend the notion of squared error loss
by defining
For this loss function the risk is the sum of the MSEs of the individual components and
the Bayes estimate is the posterior mean again. Thus 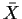 is Bayes for an improper
prior in this problem. It turns out that
is Bayes for an improper
prior in this problem. It turns out that 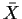 is minimax; its risk function is
the constant
is minimax; its risk function is
the constant
 .
If the dimension p of
.
If the dimension p of 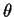 is 1 or 2 then
is 1 or 2 then
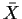 is also admissible but if
is also admissible but if  then it is inadmissible. This fact
was first demonstrated by James and Stein who produced an estimate which is better,
in terms of this risk function, for every
then it is inadmissible. This fact
was first demonstrated by James and Stein who produced an estimate which is better,
in terms of this risk function, for every  .
The ``improved'' estimator, called the
James Stein estimator is essentially never used.
.
The ``improved'' estimator, called the
James Stein estimator is essentially never used.



Richard Lockhart
1998-11-30
![]() .
We may make our decision d depend on X. A
decision rule is a function
.
We may make our decision d depend on X. A
decision rule is a function ![]() from
from ![]() to D.
We will want
to D.
We will want
![]() to be small for all
to be small for all ![]() .
Since
X is random we quantify this by averaging over X and compare procedures
.
Since
X is random we quantify this by averaging over X and compare procedures
![]() in terms of the risk function
in terms of the risk function
![]() and
pick ``the smaller one''. But typically the two functions will cross each
other and there won't be a unique `smaller one'.
and
pick ``the smaller one''. But typically the two functions will cross each
other and there won't be a unique `smaller one'.
![]() we used
we used ![]() ,
,
![]() is inadmissible if there is
a rule
is inadmissible if there is
a rule ![]() such that
such that
![]() is
is

![]() to minimize
to minimize ![]() ? The solution
lies in recognizing that
? The solution
lies in recognizing that
![]() is really a joint
density
is really a joint
density

![\begin{displaymath}r_\pi(\hat\theta) = \int \left[ \int (\hat\theta(x) - \theta)^2
\pi(\theta\vert x) d\theta \right] f(x) dx
\end{displaymath}](img43.gif)
![]() .
Imagine, for example that
.
Imagine, for example that ![]() is the true speed of sound.
I think this is around 330 metres per second and am pretty sure that I
am within 30 metres per second of the truth with that guess. I might
summarize my opinion by saying that I think
is the true speed of sound.
I think this is around 330 metres per second and am pretty sure that I
am within 30 metres per second of the truth with that guess. I might
summarize my opinion by saying that I think ![]() has a normal distribution
with mean
has a normal distribution
with mean ![]() 330 and standard deviation
330 and standard deviation ![]() .
That is, I take a
prior density
.
That is, I take a
prior density ![]() for
for ![]() to be
.
Before I make any
measurements my best guess of
to be
.
Before I make any
measurements my best guess of ![]() minimizes
minimizes

![]() is that
the measurements are unbiased and that the standard deviation of the
measurement errors is
is that
the measurements are unbiased and that the standard deviation of the
measurement errors is ![]() which I assume that we know. Thus the
model is that conditional on
which I assume that we know. Thus the
model is that conditional on ![]()
![]() are iid
are iid
![]() .
The joint density of the data and
.
The joint density of the data and ![]() is then
is then



![]() example consider
the prior density
example consider
the prior density
![]() .
This ``density'' integrates
to
.
This ``density'' integrates
to ![]() but using Bayes' theorem to compute the posterior would
give
but using Bayes' theorem to compute the posterior would
give

![]() and each real
and each real ![]() the estimate
the estimate
![]() is simply
is simply
![]() .
That is, the risk function is constant since
it does not depend on
.
That is, the risk function is constant since
it does not depend on ![]() .
Were
.
Were ![]() Bayes for a proper
prior this would prove that
Bayes for a proper
prior this would prove that ![]() is minimax. In fact this is also
true but hard to prove.
is minimax. In fact this is also
true but hard to prove.
![]() prior density
prior density


![]() is
is
![]() are iid
are iid
![]() with
with ![]() known. Consider as the improper prior for
known. Consider as the improper prior for ![]() which is constant. The
posterior density of
which is constant. The
posterior density of ![]() given X is then
given X is then
![]() .
.