


Postscript version of these notes
STAT 801 Lecture 25
Reading for Today's Lecture:
Goals of Today's Lecture:
- Do Bayesian estimation examples.
- Look at hypothesis testing as decision theory.
Today's notes
Statistical Decision Theory: examples
Example: In estimation theory to estimate a real parameter
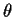 we used
we used  ,
,
and find that the risk of an estimator
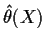 is
is
which is just the Mean Squared Error of
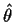 .
.
The Bayes estimate of 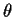 is
is
 ,
the posterior mean of
,
the posterior mean of
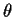 .
.
Example: In
 model with
model with  known
a common prior is
known
a common prior is
 .
The resulting posterior
distribution is Normal with posterior mean
.
The resulting posterior
distribution is Normal with posterior mean
and posterior variance
 .
.
Improper priors: When the density does not integrate
to 1 we can still follow the machinery of Bayes' formula to derive
a posterior. For instance in the
 example consider
the prior density
example consider
the prior density
 .
This ``density'' integrates
to
.
This ``density'' integrates
to  but using Bayes' theorem to compute the posterior would
give
but using Bayes' theorem to compute the posterior would
give
It is easy to see that this cancels to the limit of the case previously
done when
 giving a
giving a
 density.
That is, the Bayes estimate of
density.
That is, the Bayes estimate of  for this improper prior is
for this improper prior is  .
.
Admissibility: Bayes procedures with finite Bayes risk
and continuous risk functions are admissible. It follows that for each
 and each real
and each real  the estimate
the estimate
is admissible. That this is also true for w=1, that is, that  is admissible, is much harder to prove.
is admissible, is much harder to prove.
Minimax estimation: The risk function of  is simply
is simply
 .
That is, the risk function is constant since
it does not depend on
.
That is, the risk function is constant since
it does not depend on  .
Were
.
Were  Bayes for a proper
prior this would prove that
Bayes for a proper
prior this would prove that  is minimax. In fact this is also
true but hard to prove.
is minimax. In fact this is also
true but hard to prove.
Example: Suppose that given p X has a Binomial(n,p)
distribution. We will give p a Beta
 prior density
prior density
The joint ``density'' of X and p is
so that the posterior density of p given X is of the form
for a suitable normalizing constant c. But this is a
Beta
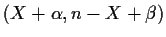 density. The mean of a Beta
density. The mean of a Beta
 distribution is
distribution is
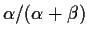 .
Thus the Bayes estimate
of p is
.
Thus the Bayes estimate
of p is
where
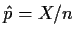 is the usual mle.
Notice that this is again a weighted average of the prior mean and
the mle. Notice also that the prior is proper for
is the usual mle.
Notice that this is again a weighted average of the prior mean and
the mle. Notice also that the prior is proper for  and
and
 .
To get w=1 we take
.
To get w=1 we take
 and use the improper
prior
and use the improper
prior
Again we learn that each
 is admissible for
is admissible for
 .
Again it is true that
.
Again it is true that  is admissible but that
our theorem is not adequate to prove this fact.
is admissible but that
our theorem is not adequate to prove this fact.
The risk function of
 is
is
which is
This risk function will be constant if the coefficients of
both p2 and of p in the risk are 0. The coefficient of
p is
-w2/n +(1-w)2
so
w=n1/2/(1+n1/2). The coefficient of p is then
w2/n -2p0(1-w)2
which will vanish if 2p0=1 or p0=1/2. Working
backwards we find that to get these values for w and p0
we require
 .
Moreover the equation
.
Moreover the equation
w2/(1-w)2 = n
gives
or
 .
The minimax estimate of
p is
.
The minimax estimate of
p is
Example: Now suppose that
 are iid
are iid
 with
with  known. Consider as the improper prior for
known. Consider as the improper prior for  which is constant. The
posterior density of
which is constant. The
posterior density of  given X is then
given X is then
 .
.
For multivariate estimation it is common to extend the notion of squared error loss
by defining
For this loss function the risk is the sum of the MSEs of
the individual components and the Bayes estimate is the
posterior mean again. Thus  is Bayes for an improper
prior in this problem. It turns out that
is Bayes for an improper
prior in this problem. It turns out that  is minimax;
its risk function is the constant
is minimax;
its risk function is the constant
 .
If the
dimension p of
.
If the
dimension p of 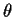 is 1 or 2 then
is 1 or 2 then  is also admissible
but if
is also admissible
but if  then it is inadmissible. This fact was first
demonstrated by James and Stein who produced an estimate which is better,
in terms of this risk function, for every
then it is inadmissible. This fact was first
demonstrated by James and Stein who produced an estimate which is better,
in terms of this risk function, for every  .
The ``improved''
estimator, called the James Stein estimator, is essentially never used.
.
The ``improved''
estimator, called the James Stein estimator, is essentially never used.
Hypothesis Testing and Decision Theory
One common decision analysis of hypothesis testing takes
 and
and
 or
more generally
or
more generally
 and
and
 for two positive
constants
for two positive
constants  and
and  .
We make the decision space convex
by allowing a decision to be a probability measure on D. Any such measure
can be specified by
.
We make the decision space convex
by allowing a decision to be a probability measure on D. Any such measure
can be specified by
 so
so
![${\cal D} =[0,1]$](img60.gif) .
The
loss function of
.
The
loss function of
![$\delta\in[0,1]$](img61.gif) is
is
Simple hypotheses: A prior is just two numbers  and
and 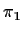 which are non-negative and sum to 1. A procedure is a map
from the data space to
which are non-negative and sum to 1. A procedure is a map
from the data space to  which is exactly what a test function was.
The risk function of a procedure
which is exactly what a test function was.
The risk function of a procedure  is a pair of numbers:
is a pair of numbers:
and
We find
and
The Bayes risk of  is
is
We saw in the hypothesis testing section that this is minimized
by
which is a likelihood ratio test. These tests are Bayes
and admissible. The risk is constant if
 ;
you can use this to find the minimax test in this context.
;
you can use this to find the minimax test in this context.
Composite hypotheses:



Richard Lockhart
1998-12-02
![]() we used
we used ![]() ,
,
![]() is
is
![]() ,
the posterior mean of
,
the posterior mean of
![]() .
.
![]() model with
model with ![]() known
a common prior is
known
a common prior is
![]() .
The resulting posterior
distribution is Normal with posterior mean
.
The resulting posterior
distribution is Normal with posterior mean

![]() example consider
the prior density
example consider
the prior density
![]() .
This ``density'' integrates
to
.
This ``density'' integrates
to ![]() but using Bayes' theorem to compute the posterior would
give
but using Bayes' theorem to compute the posterior would
give

![]() and each real
and each real ![]() the estimate
the estimate
![]() is simply
is simply
![]() .
That is, the risk function is constant since
it does not depend on
.
That is, the risk function is constant since
it does not depend on ![]() .
Were
.
Were ![]() Bayes for a proper
prior this would prove that
Bayes for a proper
prior this would prove that ![]() is minimax. In fact this is also
true but hard to prove.
is minimax. In fact this is also
true but hard to prove.
![]() prior density
prior density



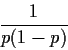
![]() is
is

![]() are iid
are iid
![]() with
with ![]() known. Consider as the improper prior for
known. Consider as the improper prior for ![]() which is constant. The
posterior density of
which is constant. The
posterior density of ![]() given X is then
given X is then
![]() .
.
![]() and
and
![]() or
more generally
or
more generally
![]() and
and
![]() for two positive
constants
for two positive
constants ![]() and
and ![]() .
We make the decision space convex
by allowing a decision to be a probability measure on D. Any such measure
can be specified by
.
We make the decision space convex
by allowing a decision to be a probability measure on D. Any such measure
can be specified by
![]() so
so
![]() .
The
loss function of
.
The
loss function of
![]() is
is
![]() and
and ![]() which are non-negative and sum to 1. A procedure is a map
from the data space to
which are non-negative and sum to 1. A procedure is a map
from the data space to ![]() which is exactly what a test function was.
The risk function of a procedure
which is exactly what a test function was.
The risk function of a procedure ![]() is a pair of numbers:
is a pair of numbers: