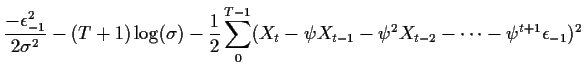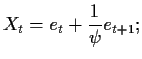Postscript version of these notes
STAT 804: Notes on Lecture 9
Fitting higher order autoregressions
For the model
we will use conditional likelihood again. Let 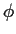 denote the
vector
denote the
vector
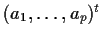 . Now we condition
on the first
. Now we condition
on the first 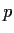 values of
values of 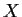 and use
If we estimate
and use
If we estimate 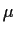 using
using 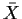 we find that we are trying
to maximize
To estimate
we find that we are trying
to maximize
To estimate
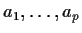 then we merely minimize the sum of squares
This is a straightforward regression problem. We regress the response
vector
on the design matrix
then we merely minimize the sum of squares
This is a straightforward regression problem. We regress the response
vector
on the design matrix
An alternative to estimating 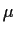 by
by 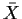 is to define
is to define
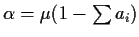 and then recognize that
and then recognize that
is maximized by regressing the vector
on the design matrix
From
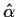 and
and 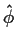 we would get an estimate for
we would get an estimate for
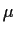 by
by
Notice that if we put
then
and if
then
so that the normal equations (from least squares)
are nearly the Yule-Walker equations again.
Full maximum likelihood
To compute a full mle of
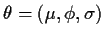 you generally begin by finding preliminary estimates
you generally begin by finding preliminary estimates
 say by one of the conditional likelihood
methods above and then iterate via Newton-Raphson or
some other scheme for numerical maximization of the
log-likelihood.
say by one of the conditional likelihood
methods above and then iterate via Newton-Raphson or
some other scheme for numerical maximization of the
log-likelihood.
Fitting  models
models
Here we consider the model with known mean (generally this
will mean we estimate
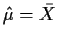 and subtract the mean
from all the observations):
and subtract the mean
from all the observations):
In general 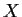 has a
has a
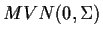 distribution and, letting
distribution and, letting
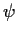 denote the vector of
denote the vector of 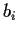 s we find
s we find
Here 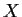 denotes the column vector of all the data.
As an example consider
denotes the column vector of all the data.
As an example consider 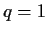 so that
It is not so easy to work with the determinant and inverse of matrices
like this. Instead we try to mimic the conditional inference approach
above but with a twist; we now condition on something we haven't observed
--
so that
It is not so easy to work with the determinant and inverse of matrices
like this. Instead we try to mimic the conditional inference approach
above but with a twist; we now condition on something we haven't observed
--
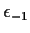 .
.
Notice that
Now imagine that the data were actually
Then the same idea we used for an 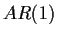 would give
would give
The parameters are listed in the conditions in this formula merely
to indicate which terms depend on which parameters. For
Gaussian 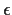 s the terms in this likelihood are squares
as usual (plus logarithms of
s the terms in this likelihood are squares
as usual (plus logarithms of 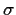 ) leading to
) leading to
We will estimate the parameters by maximizing this function
after getting rid of
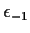 somehow.
somehow.
Method A: Put
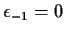 since 0 is
the most probable value and maximize
since 0 is
the most probable value and maximize
Notice that for large 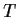 the coefficients of
the coefficients of
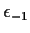 are close to 0 for most
are close to 0 for most 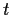 and the remaining few terms are
negligible relatively to the total.
and the remaining few terms are
negligible relatively to the total.
Method B: Backcasting is the process of
guessing
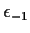 on the basis of the data; we replace
on the basis of the data; we replace
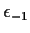 in the log likelihood by
in the log likelihood by
E
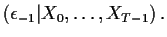
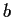 and
and 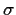 .
.
We will use the EM algorithm to solve this problem.
The algorithm can be applied when we have (real or imaginary)
missing data. Suppose the data we have is 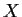 ; some other data
we didn't get is
; some other data
we didn't get is 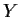 and
and  . It often happens that we can
think of a
. It often happens that we can
think of a 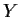 we didn't observe in such a way that the likelihood
for the whole data set
we didn't observe in such a way that the likelihood
for the whole data set 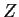 would be simple. In that case we can
try to maximize the likelihood for
would be simple. In that case we can
try to maximize the likelihood for 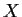 by following a two step
algorithm first discussed in detail by Dempster, Laid and Rubin.
This algorithm has two steps:
by following a two step
algorithm first discussed in detail by Dempster, Laid and Rubin.
This algorithm has two steps:
- The E or Estimation step. We ``estimate''
the missing data
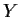 by computing
E
by computing
E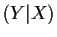 . Technically,
we are supposed to estimate the likelihood function based on
. Technically,
we are supposed to estimate the likelihood function based on 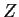 .
Factor the density of
.
Factor the density of 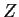 as
and take logs to get
We actually estimate the log conditional density (which is
a function of
as
and take logs to get
We actually estimate the log conditional density (which is
a function of 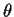 ) by computing
) by computing
E
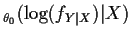
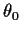 on E. This indicates
that you have to know the parameter to compute the conditional
expectation. Notice too that there is another
on E. This indicates
that you have to know the parameter to compute the conditional
expectation. Notice too that there is another 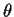 in the
conditional expectation - the log conditional density has
a parameter in it.
in the
conditional expectation - the log conditional density has
a parameter in it.
- We then maximize our estimate of
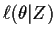 to get
a new value
to get
a new value 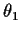 for
for 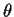 . Go back to step 1 with this
. Go back to step 1 with this
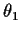 replacing
replacing 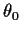 and iterate.
and iterate.
To get started we need a preliminary estimate. Now look at our
problem. In our case the quantity 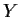 is
is
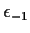 .
Rather than work with the log-likelihood directly we work with
.
Rather than work with the log-likelihood directly we work with
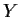 . Our preliminary estimate of
. Our preliminary estimate of 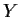 is 0. We use this value
to estimate
is 0. We use this value
to estimate 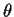 as above getting an estimate
as above getting an estimate 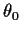 .
Then we compute
E
.
Then we compute
E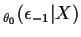 and
replace
and
replace
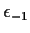 in the log-likelihood above by this
conditional expectation. Then iterate. This process of guessing
in the log-likelihood above by this
conditional expectation. Then iterate. This process of guessing
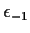 is called backcasting.
is called backcasting.
Summary
- The log likelihood based on
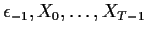 is
is
- Put
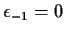 in this formula and estimate
in this formula and estimate
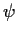 by minimizing
where
for
by minimizing
where
for
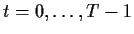 .
.
- Now compute
E
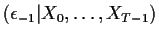 Box, Jenkins and Reinsel presents an algorithm to do so based
on the fact that there are actually two MA representations of
corresponding to a given covariance function (the invertible
one and a non-invertible one). The non-invertible representation
is
this
form can be used to carry out the computation of the
conditional expection.
Box, Jenkins and Reinsel presents an algorithm to do so based
on the fact that there are actually two MA representations of
corresponding to a given covariance function (the invertible
one and a non-invertible one). The non-invertible representation
is
this
form can be used to carry out the computation of the
conditional expection.
- Iterate, re-estimating
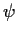 and recomputing the
backcast value of
and recomputing the
backcast value of
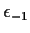 if needed.
if needed.



Richard Lockhart
2001-09-30
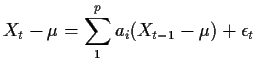
![$\displaystyle \ell_c(\phi,\mu,\sigma) = -\frac{1}{2\sigma^2}
\sum_p^{T-1} \left[ X_t-\mu - \sum_1^p a_i(X_{t-i} - \mu)\right]^2
-(T-p)\log(\sigma)
$](img6.gif)
![$\displaystyle -\frac{1}{2\sigma^2}
\sum_p^{T-1} \left[ X_t-\bar{X} - \sum_1^p a_i(X_{t-i} - \bar{X})\right]^2
-(T-p)\log(\sigma)
$](img9.gif)
![$\displaystyle \sum_p^{T-1} \hat\epsilon_t^2 = \sum_p^{T-1} \left[ X_t-\bar{X} - \sum_1^p
a_i(X_{t-i} - \bar{X})\right]^2
$](img11.gif)
![$\displaystyle \left[\begin{array}{c} X_p -\bar{X} \\ \vdots \\ X_{T-1} -\bar{X} \end{array} \right]
$](img12.gif)
![$\displaystyle \left[\begin{array}{ccc}
X_{p-1} -\bar{X}& \cdots & X_0 -\bar{X}
...
...
\vdots
\\
X_{T-2} -\bar{X}& \cdots & X_{T-p-1} -\bar{X}
\end{array}\right]
$](img13.gif)
![]() by
by ![]() is to define
is to define
![]() and then recognize that
and then recognize that
![$\displaystyle \ell(\alpha,\phi,\sigma) = -\frac{1}{2\sigma^2}
\sum_p^{T-1} \left[ X_t-\alpha - \sum_1^p a_iX_{t-i}\right]^2
-(T-p)\log(\sigma)
$](img15.gif)
![$\displaystyle \left[\begin{array}{c} X_p \\ \vdots \\ X_{T-1} \end{array} \right]
$](img16.gif)
![$\displaystyle \left[\begin{array}{ccc}
X_{p-1} & \cdots & X_0
\\
\vdots &
\vdots & \vdots
\\
X_{T-2} & \cdots & X_{T-p-1}
\end{array}\right]
$](img17.gif)

![$\displaystyle Z=\left[\begin{array}{ccc}
X_{p-1} -\bar{X}& \cdots & X_0 -\bar{X...
...&
\vdots
\\
X_{T-2} -\bar{X}& \cdots & X_{T-p-1} -\bar{X}
\end{array}\right]
$](img21.gif)
![$\displaystyle Z^tZ \approx T \left[\begin{array}{cccc}
\hat{C}(0) & \hat{C}(1) ...
...ots & \cdots
\\
\cdots & \cdots & \hat{C}(1) & \hat{C}(0)
\end{array}\right]
$](img22.gif)
![$\displaystyle Y=\left[\begin{array}{c} X_p -\bar{X} \\ \vdots \\ X_{T-1} -\bar{X}
\end{array} \right]
$](img23.gif)
![$\displaystyle Z^tY \approx T \left[\begin{array}{c} \hat{C}(1) \\ \vdots \\ \hat{C}(p)
\end{array}\right]
$](img24.gif)
![]() you generally begin by finding preliminary estimates
you generally begin by finding preliminary estimates
![]() say by one of the conditional likelihood
methods above and then iterate via Newton-Raphson or
some other scheme for numerical maximization of the
log-likelihood.
say by one of the conditional likelihood
methods above and then iterate via Newton-Raphson or
some other scheme for numerical maximization of the
log-likelihood.
![]() and subtract the mean
from all the observations):
and subtract the mean
from all the observations):
![]() has a
has a
![]() distribution and, letting
distribution and, letting
![]() denote the vector of
denote the vector of ![]() s we find
s we find
![$\displaystyle \ell(\psi,\sigma) = -\frac{1}{2}\left[\log(\det(\Sigma))
- X^T \Sigma^{-1} X\right]
$](img34.gif)
![$\displaystyle \Sigma = \left[\begin{array}{ccccc}
\sigma^2(1+b_1^2) & -b_1\sigm...
...
\\
0 & \cdots & \cdots & -b_1\sigma^2& \sigma^2(1+b_1^2)
\end{array}\right]
$](img36.gif)
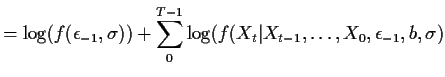
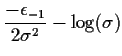
![$\displaystyle - \sum_0^{T-1} \left[\frac{1}{2} (X_t - \psi X_{t-1} - \psi^2 X_{t-2} - \cdots -\psi^{t+1} \epsilon_{-1})^2+\log(\sigma)\right]$](img58.gif)
![]() since 0 is
the most probable value and maximize
since 0 is
the most probable value and maximize
![$\displaystyle -T\log(\sigma) - \frac{1}{2\sigma^2} \sum_0^{T-1} \left[X_t - \psi X_{t-1}
- \psi^2 X_{t-2} - \cdots -\psi^{t}X_0\right]^2
$](img60.gif)
![]() on the basis of the data; we replace
on the basis of the data; we replace
![]() in the log likelihood by
in the log likelihood by
![]() ; some other data
we didn't get is
; some other data
we didn't get is ![]() and
and ![]() . It often happens that we can
think of a
. It often happens that we can
think of a ![]() we didn't observe in such a way that the likelihood
for the whole data set
we didn't observe in such a way that the likelihood
for the whole data set ![]() would be simple. In that case we can
try to maximize the likelihood for
would be simple. In that case we can
try to maximize the likelihood for ![]() by following a two step
algorithm first discussed in detail by Dempster, Laid and Rubin.
This algorithm has two steps:
by following a two step
algorithm first discussed in detail by Dempster, Laid and Rubin.
This algorithm has two steps:
![]() is
is
![]() .
Rather than work with the log-likelihood directly we work with
.
Rather than work with the log-likelihood directly we work with
![]() . Our preliminary estimate of
. Our preliminary estimate of ![]() is 0. We use this value
to estimate
is 0. We use this value
to estimate ![]() as above getting an estimate
as above getting an estimate ![]() .
Then we compute
E
.
Then we compute
E![]() and
replace
and
replace
![]() in the log-likelihood above by this
conditional expectation. Then iterate. This process of guessing
in the log-likelihood above by this
conditional expectation. Then iterate. This process of guessing
![]() is called backcasting.
is called backcasting.