The model applies equally to a string fixed at both ends or a tube open at both ends, at least in terms of the resonant frequencies all being harmonics of the fundamental. If the sample is negated before being fed back into the delay line, the resulting change of phase models a tube closed at one end, which results in only the odd harmonics being resonant, and lowers the fundamental frequency by an octave, since the negation effectively doubles the length of the delay line. For the basic model, the fundamental resonance equals
SR / (p + 1/2)
where SR is the sampling rate, and p is the length of the delay line.
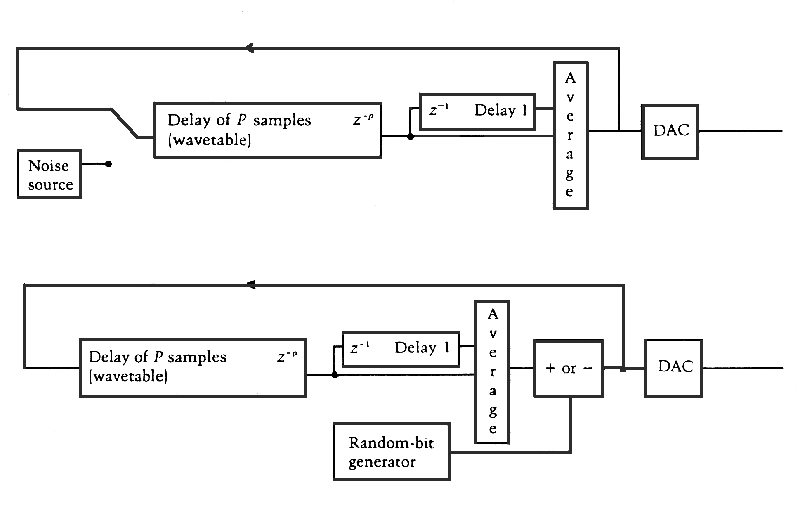
However, since the technique models a resonating tube as well as a fixed string, it is equally suited for processing sampled sound. Because an ongoing signal activates the resonator, rather than an initial noise burst, a feedback gain factor must be used to prevent amplitude overflow and to control the amount of resonance in the resulting sound. The current real-time PODX system implementation offers a choice of delay line configurations (single, in parallel or series), plus the options of adding a comb filter (to add or subtract a delayed signal) and signal negation (which lowers the fundamental frequency by an octave and produces odd harmonics).
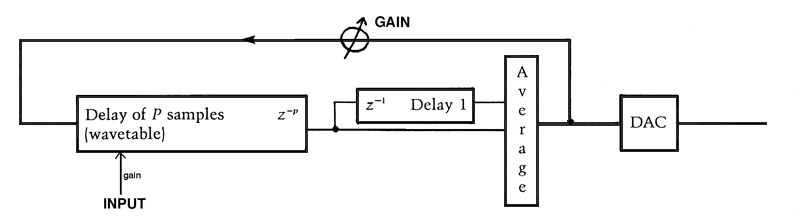
Particularly interesting effects occur when the length of the Karplus-Strong delay and the comb filter delay are related by simple ratios. Each delay line has real-time control over its length, and hence its tuning, up to a maximum of 511 samples. The user also controls the feedback level which can be finely adjusted to ride just below saturation, in combination with the input amplitude which can be lowered to facilitate higher feedback levels. The use of sample negation also makes it easier to control high feedback levels since the length of the feedback loop is essentially doubled.
The complex behaviour of these resonators, particularly when driven to their maximum feedback level (termed hyper-resonance) cannot be tracked by the ear at normal speed, compared to when such sounds are time-stretched, using the real-time granulation technique described by Truax (1994) with the DMX-1000 signal processor. Such processing lengthens the decay of the resonance to an arbitrary duration, hence suggesting a very large space, while keeping the resonant frequencies intact.
That is, resonant frequencies associated with relatively short tubes appear to emanate from spaces with much larger volumes. Vocal sounds subjected to this processing resemble 'overtone singing' in a reverberant cathedral, because the resonant frequencies are strong enough to be heard as pitches. The addition of simple harmonization at the granulation stage, such as an octave lower, enriches the sound further and gives the impression of a choir.
The technique is prominently used in the works Inside, Powers of Two: The Artist, Wings of Fire, Androgyne, Mon Amour, Pacific Fanfare, Powers of Two: The Sibyl, Powers of Two: Beyond, PendlerdrÝm, and Sequence of Earlier Heaven. Sound examples are provided on the WSP Database (contact Barry at truax@sfu.ca for guest access).
References:
Karplus, K. & A. Strong, 1983. Digital synthesis of plucked string and drum timbres. Computer Music Journal, 7(2).
Truax, B. 1994. Discovering inner complexity: Time-shifting and transposition with a real-time granulation technique. Computer Music Journal, 18(2), 38-48.