Example 19.5: Ordinal Relations Among Factor Loadings

The CALIS Procedure

Example 19.5: Ordinal Relations Among Factor Loadings

McDonald (1980) uses the same data set to compute a factor analysis with ordinally constrained factor loadings. The results of the linearly constrained factor analysis show that the loadings of the two factors are ordered as 2, 1, 3, 4, 6, 5. McDonald (1980) then tests the hypothesis that the factor loadings are all nonnegative and can be ordered in the following manner:

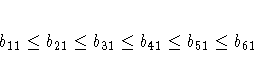
$b_{11} \le b_{21} \le b_{31} \le b_{41} \le b_{51} \le b_{61}$

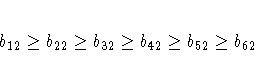
$b_{12} \ge b_{22} \ge b_{32} \ge b_{42} \ge b_{52} \ge b_{62}$

This example is recomputed by PROC CALIS to illustrate a further application of the COSAN model statement combined with program statements. The same identification problem as in Example 19.4 occurs here. The following model specification describes an unidentified model:

   proc calis data=Kinzer method=max outram=ram tech=nr nobs=326;        
   Title2 "Ordinally Related Factor Analysis, (Mcdonald,1980)";          
   Title3 "Identification Problem";                                      
   Cosan F(8,Gen) * I(8,Ide);                                            
      MATRIX F                                                            
         [,1]  = x1-x6,                                                     
         [,2]  = x7-x12,                                                    
         [1,3] = x13-x18;                                                  
      PARAMETERS t1-t10=1.;                                               
         x2  = x1  + t1  * t1;                                               
         x3  = x2  + t2  * t2;                                               
         x4  = x3  + t3  * t3;                                               
         x5  = x4  + t4  * t4;                                               
         x6  = x5  + t5  * t5;                                               
         x11 = x12 + t6  * t6;                                               
         x10 = x11 + t7  * t7;                                               
         x9  = x10 + t8  * t8;                                               
         x8  = x9  + t9  * t9;                                               
         x7  = x8  + t10 * t10;                                              
      Bounds x13-x18 >= 0.;                                               
      Vnames F Fact1 Fact2 Uvar1-Uvar6;                                   
   run;

You can specify the same model with the LINCON statement:

   proc calis data=Kinzer method=max tech=lm edf=325;      
      Title3 "Identified Problem 2";                         
      cosan f(8,gen)*I(8,ide);                              
      matrix F                                              
         [,1]  = x1-x6,                                       
         [,2]  = x7-x12,                                      
         [1,3] = x13-x18;                                    
      lincon  x1  <= x2,                                    
              x2  <= x3,                                    
              x3  <= x4,                                    
              x4  <= x5,                                    
              x5  <= x6,                                    
              x7  >= x8,                                    
              x8  >= x9,                                    
              x9  >= x10,                                   
              x10 >= x11,                                   
              x11 >= x12;                                   
      Bounds x13-x18 >= 0.;                                 
      Vnames F Fact1 Fact2 Uvar1-Uvar6;                     
   run;

To have an identified model, the loading, b₁₁ (x1), is fixed at 0. The information in the OUTRAM= data set (the data set ram), produced by the unidentified model, can be used to specify the identified model. However, because x1 is now a fixed constant in the identified model, it should not have a parameter name in the new analysis. Thus, the data set ram is modified as follows:

   data ram2(type=ram); set ram;                                              
      if _name_ = 'x1' then do;                                              
         _name_ = ' '; _estim_ = 0.;                                          
      end;                                                                   
   run;

The data set ram2 is now an OUTRAM= data set in which x1 is no longer a parameter. PROC CALIS reads the information (that is, the set of parameters and the model specification) in the data set ram2 for the identified model. As displayed in the following code, you can use the PARMS statement to specify the desired ordinal relationships between the parameters.

                                                               
   proc calis data=Kinzer method=max inram=ram2 tech=nr nobs=326;     
      title2 "Ordinally Related Factor Analysis, (Mcdonald,1980)";               
      title3 "Identified Model with X1=0";                                       
      parms t1-t10= 10 * 1.;                                                   
         x2  =     + t1  * t1;                                                    
         x3  = x2  + t2  * t2;                                                    
         x4  = x3  + t3  * t3;                                                    
         x5  = x4  + t4  * t4;                                                    
         x6  = x5  + t5  * t5;                                                    
         x11 = x12 + t6  * t6;                                                    
         x10 = x11 + t7  * t7;                                                    
         x9  = x10 + t8  * t8;                                                    
         x8  = x9  + t9  * t9;                                                    
         x7  = x8  + t10 * t10;                                                   
      bounds x13-x18 >= 0.;                                                    
   run;

Selected output for the identified model is displayed in Output 19.5.1.

Output 19.5.1: Factor Analysis with Ordinal Constraints

Data Matrix of Kinzer & Kinzer, see GUTTMAN (1957)

Ordinally Related Factor Analysis, (Mcdonald,1980)

Identified Model with X1=0

The CALIS Procedure

Covariance Structure Analysis: Maximum Likelihood Estimation

Parameter Estimates	17
Functions (Observations)	21
Lower Bounds	6
Upper Bounds	0

Optimization Start
Active Constraints	0	Objective Function	5.2552270182
Max Abs Gradient Element	0.8821788922

Iteration	Restarts	Function Calls	Active Constraints	Objective Function	Objective Function Change	Max Abs Gradient Element	Ridge	Ratio Between Actual and Predicted Change
1	0	2	0	3.14901	2.1062	1.0712	0	2.226
2	0	3	0	1.42725	1.7218	1.0902	0	2.064
3	0	4	0	0.41661	1.0106	0.7472	0	1.731
4	0	5	0	0.09260	0.3240	0.3365	0	1.314
5	0	6	0	0.09186	0.000731	0.3880	0	0.0123
6	0	8	0	0.04570	0.0462	0.2870	0.0313	0.797
7	0	10	0	0.03269	0.0130	0.0909	0.0031	0.739
8	0	16	0	0.02771	0.00498	0.0890	0.0800	0.682
9	0	17	0	0.02602	0.00168	0.0174	0.0400	0.776
10	0	19	0	0.02570	0.000323	0.0141	0.0800	0.630
11	0	21	0	0.02560	0.000103	0.00179	0.160	1.170
12	0	23	0	0.02559	7.587E-6	0.000670	0.160	1.423
13	0	24	0	0.02559	2.993E-6	0.000402	0.0400	1.010
14	0	27	0	0.02559	1.013E-6	0.000206	0.160	1.388
15	0	28	0	0.02559	1.889E-7	0.000202	0.0400	0.530
16	0	30	0	0.02559	1.803E-7	0.000097	0.0800	0.630
17	0	32	0	0.02559	4.845E-8	0.000035	0.160	1.340
18	0	33	0	0.02559	1.837E-9	0.000049	0.0400	0.125
19	0	35	0	0.02559	9.39E-9	0.000024	0.0800	0.579
20	0	37	0	0.02559	2.558E-9	6.176E-6	0.160	1.305

Optimization Results
Iterations	20	Function Calls	38
Jacobian Calls	21	Active Constraints	0
Objective Function	0.0255871615	Max Abs Gradient Element	6.1764582E-6
Ridge	0.04	Actual Over Pred Change	1.3054374955

ABSGCONV convergence criterion satisfied.

Data Matrix of Kinzer & Kinzer, see GUTTMAN (1957)

Ordinally Related Factor Analysis, (Mcdonald,1980)

Identified Model with X1=0

The CALIS Procedure

Covariance Structure Analysis: Maximum Likelihood Estimation

Fit Function	0.0256
Goodness of Fit Index (GFI)	0.9916
GFI Adjusted for Degrees of Freedom (AGFI)	0.9557
Root Mean Square Residual (RMR)	0.0180
Parsimonious GFI (Mulaik, 1989)	0.2644
Chi-Square	8.3158
Chi-Square DF	4
Pr > Chi-Square	0.0807
Independence Model Chi-Square	682.87
Independence Model Chi-Square DF	15
RMSEA Estimate	0.0576
RMSEA 90% Lower Confidence Limit	.
RMSEA 90% Upper Confidence Limit	0.1133
ECVI Estimate	0.1325
ECVI 90% Lower Confidence Limit	.
ECVI 90% Upper Confidence Limit	0.1711
Probability of Close Fit	0.3399
Bentler's Comparative Fit Index	0.9935
Normal Theory Reweighted LS Chi-Square	8.2901
Akaike's Information Criterion	0.3158
Bozdogan's (1987) CAIC	-18.8318
Schwarz's Bayesian Criterion	-14.8318
McDonald's (1989) Centrality	0.9934
Bentler & Bonett's (1980) Non-normed Index	0.9758
Bentler & Bonett's (1980) NFI	0.9878
James, Mulaik, & Brett (1982) Parsimonious NFI	0.2634
Z-Test of Wilson & Hilferty (1931)	1.4079
Bollen (1986) Normed Index Rho1	0.9543
Bollen (1988) Non-normed Index Delta2	0.9936
Hoelter's (1983) Critical N	372

Data Matrix of Kinzer & Kinzer, see GUTTMAN (1957)

Ordinally Related Factor Analysis, (Mcdonald,1980)

Identified Model with X1=0

The CALIS Procedure

Covariance Structure Analysis: Maximum Likelihood Estimation

Estimated Parameter Matrix F[6:8] Standard Errors and t Values General Matrix
	Fact1	Fact2	Uvar1	Uvar2	Uvar3	Uvar4	Uvar5	Uvar6
Obs1	0 0 0	0.7101 0.0435 16.3317 <x7>	0.7131 0.0404 17.6427 [x13]	0 0 0	0 0 0	0 0 0	0 0 0	0 0 0
Obs2	0.0261 0.0875 0.2977 <x2>	0.7101 0.0435 16.3317 <x8>	0 0 0	0.6950 0.0391 17.7571 [x14]	0 0 0	0 0 0	0 0 0	0 0 0
Obs3	0.2382 0.0851 2.7998 <x3>	0.6827 0.0604 11.3110 <x9>	0 0 0	0 0 0	0.6907 0.0338 20.4239 [x15]	0 0 0	0 0 0	0 0 0
Obs4	0.3252 0.0823 3.9504 <x4>	0.6580 0.0621 10.5950 <x10>	0 0 0	0 0 0	0 0 0	0.6790 0.0331 20.5361 [x16]	0 0 0	0 0 0
Obs5	0.5395 0.0901 5.9887 <x5>	0.5528 0.0705 7.8359 <x11>	0 0 0	0 0 0	0 0 0	0 0 0	0.6249 0.0534 11.7052 [x17]	0 0 0
Obs6	0.5395 0.0918 5.8776 <x6>	0.4834 0.0726 6.6560 [x12]	0 0 0	0 0 0	0 0 0	0 0 0	0 0 0	0.7005 0.0524 13.3749 [x18]

Data Matrix of Kinzer & Kinzer, see GUTTMAN (1957)

Ordinally Related Factor Analysis, (Mcdonald,1980)

Identified Model with X1=0

The CALIS Procedure

Covariance Structure Analysis: Maximum Likelihood Estimation

Additional PARMS and Dependent Parameters
The Number of Dependent Parameters is 10
Parameter	Estimate	Standard Error	t Value
t1	0.16143	0.27111	0.60
t2	0.46060	0.09289	4.96
t3	0.29496	0.13702	2.15
t4	0.46297	0.10756	4.30
t5	0.0000522	1311	0.00
t6	0.26347	0.12203	2.16
t7	0.32430	0.09965	3.25
t8	0.15721	0.21134	0.74
t9	0.16543	0.20537	0.81
t10	-4.2528E-7	0.47736	-0.00
x7	0.71007	0.04348	16.33
x2	0.02606	0.08753	0.30
x8	0.71007	0.04348	16.33
x3	0.23821	0.08508	2.80
x9	0.68270	0.06036	11.31
x4	0.32521	0.08232	3.95
x10	0.65799	0.06210	10.60
x5	0.53955	0.09009	5.99
x11	0.55282	0.07055	7.84
x6	0.53955	0.09180	5.88

By fixing the loading b₁₁ (x1) to constant 0, you obtain $\chi^2 = 8.316$ on df = 4 (p < .09). McDonald reports the same $\chi^2$ value, but on df=3, and thus, he obtains a smaller p-value. An analysis without the fixed loading shows typical signs of an unidentified problem: after more iterations it leads to a parameter set with a $\chi^2$ value of 8.174 on df=3. A singular Hessian matrix occurs.

The singular Hessian matrix of the unidentified problem slows down the convergence rate of the Levenberg-Marquardt algorithm considerably. Compared to the unidentified problem with 30 iterations, the identified problem needs only 20 iterations. Note that the number of iterations may depend on the precision of the processor.

The same model can also be specified using the LINCON statement for linear constraints:

   proc calis data=Kinzer method=max tech=lm edf=325;   
      Title3 "Identified Model 2";                        
      cosan f(8,gen)*I(8,ide);                           
      matrix f                                           
         [,1]  = 0. x2-x6,                                 
         [,2]  = x7-x12,                                   
         [1,3] = x13-x18;                                 



      lincon  x2  <= x3,                                 
              x3  <= x4,                                 
              x4  <= x5,                                 
              x5  <= x6,                                 
              x7  >= x8,                                 
              x8  >= x9,                                 
              x9  >= x10,                                
              x10 >= x11,                                
              x11 >= x12;                                
      bounds x2 x13-x18 >= 0.;                           
   run;

Chapter Contents
Previous
Next
Top