Testing Linear Hypotheses about the Regression Coefficients
Linear hypotheses for 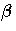 are
expressed in matrix form as
are
expressed in matrix form as
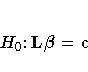
where L is a matrix of coefficients for the linear hypotheses, and
c is a vector of constants.
The vector of regression coefficients 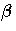 includes slope parameters
as well as intercept parameters.
The Wald chi-square statistic for testing
H0 is computed as
includes slope parameters
as well as intercept parameters.
The Wald chi-square statistic for testing
H0 is computed as
![\chi^2_{W} = (L\hat{{\beta}}- c)' [{L\hat{V}(\hat{{\beta}})L'}]^{-1} (L\hat{{\beta}}- c)](images/lgseq219.gif)
where  is the estimated
covariance matrix. Under H0,
is the estimated
covariance matrix. Under H0,  has an asymptotic
chi-square distribution with r degrees of freedom,
where r is the rank of L.
has an asymptotic
chi-square distribution with r degrees of freedom,
where r is the rank of L.
Copyright © 1999 by SAS Institute Inc., Cary, NC, USA. All rights reserved.
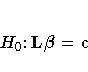
![\chi^2_{W} = (L\hat{{\beta}}- c)' [{L\hat{V}(\hat{{\beta}})L'}]^{-1} (L\hat{{\beta}}- c)](images/lgseq219.gif)