


Postscript version of this file
STAT 380 Lecture 3
Reading for Today's Lecture: Chapters 1, 2 and 3
of Ross.
Today's lecture Summary
- Example to review
- basic probability: sample space, events, random variables,
expected value
- standard distributions: Binomial, Geometric, Poisson
- conditional probability, independence
- Baye's rule
- Introduce first step analysis
Example 3: Survival of family names. Traditionally: family
name follows sons. Given man at end of 20th century. Probability
descendant (male) with same last name alive at end of 21st century?
or end of 30th century?
Simplified model: count generations not years. Compute probability,
of survival of name for n generations.
Technically easier to compute qn, probability of extinction by
generation n.
Useful rvs:
Event of interest:
Break up En:
Now look at the event
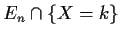 .
Let
.
Let

Then
Now add modelling assumptions:
- 1.
- Given (conditional on) X=k the events
Bj,n-1 are independent. In other words: one son's
descendants don't affect other sons' descendants.
- 2.
- Given X=k the probability of Bj,n-1 is qn-1.
In other words: sons are just like the parent.
Now add notation
P(X=k) = pk.
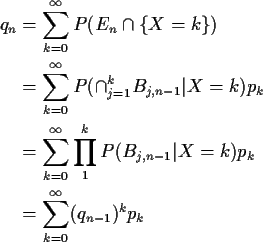
Probability generating function:
We have found
q1 = p0
and
Notice that
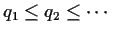 so that the limit of
the qn, say
so that the limit of
the qn, say 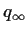 ,
must exist and (because
,
must exist and (because 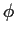 is
continuous)
solve
is
continuous)
solve
Special cases
Geometric Distribution: Assume
(X is number of failures before first success. Trials are
Bernoulli; 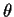 is probability of success.)
is probability of success.)
Then
![\begin{align*}\phi(s) & = \sum_0^\infty s^k (1-\theta)^k \theta
\\
& = \theta \...
...fty \left[s(1-\theta)\right]^k
\\
& = \frac{\theta}{1-s(1-\theta)}
\end{align*}](img19.gif)
Set
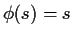 to get
to get
Two roots are
One of the roots is 1; the other is
If
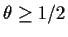 the only root which is a probability is 1 and
the only root which is a probability is 1 and
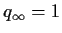 .
If
.
If
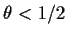 then in fact
then in fact
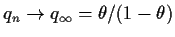 .
.
Binomial(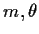 ): If
): If
then
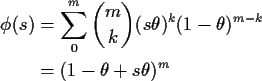
The equation 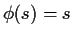 has two roots. One is 1. The other is
less than 1 if and only if
has two roots. One is 1. The other is
less than 1 if and only if
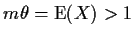 .
.
Poisson(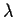 ): Now
): Now
and
The equation
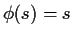 has two roots. One is 1. The other
is less than 1 if and only if
has two roots. One is 1. The other
is less than 1 if and only if
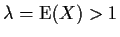 .
.
Important Points:
- Use of conditioning.
- Approximate nature of modelling assumptions
- Key assumptions of conditional independence, homogeneity



Richard Lockhart
2000-10-02
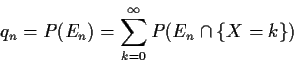
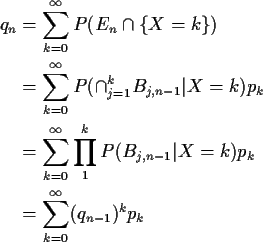
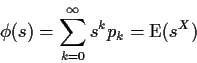
![\begin{align*}\phi(s) & = \sum_0^\infty s^k (1-\theta)^k \theta
\\
& = \theta \...
...fty \left[s(1-\theta)\right]^k
\\
& = \frac{\theta}{1-s(1-\theta)}
\end{align*}](img19.gif)
![]() to get
to get
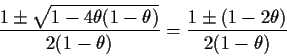
![]() ): If
): If
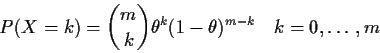
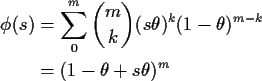
![]() ): Now
): Now