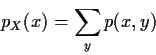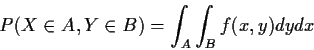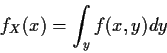Postscript version of this file

STAT 380 Lecture 4

Reading for Today's Lecture: Chapters 2, 3

Goals of Today's Lecture:

• Review properties of expectation

• Introduce conditional expectation

Example 3: Mean values

Z_n = total number of sons in generation n.

Z₀=1 for convenience.

Compute ${\rm E}(Z_n)$.

Recall definition of expected value:

If X is discrete then

$${\rm E}(X) = \sum_x x P(X=x)$$

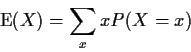
If X is absolutely continuous then

$${\rm E}(X) = \int_{-\infty}^\infty x f(x) dx$$

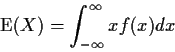
Theorem: If Y=g(X), X has density f then

$${\rm E}(Y) = {\rm E}(g(X)) =\int g(x) f(x) dx$$

Key properties of ${\rm E}$:

1: If $X\ge 0$ then ${\rm E}(X) \ge 0$. Equals iff P(X=0)=1.

2: ${\rm E}(aX+bY) = a{\rm E}(X) +b{\rm E}(Y)$.

3: If $0 \le X_1 \le X_2 \le \cdots$ then

$${\rm E}(\lim X_n) = \lim {\rm E}(X_n)$$

4: ${\rm E}(1) = 1$.

Conditional Expectations

If X, Y, two discrete random variables then

$${\rm E}(Y\vert X=x) = \sum_y y P(Y=y\vert X=x)$$

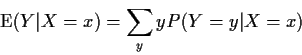
Extension to absolutely continuous case:

Joint pmf of X and Y is defined as

p(x,y) = P(X=x,Y=y)

Notice: The pmf of X is

$$p_X(x) = \sum_y p(x,y)$$

Analogue for densities: joint density of X,Y is

$$f(x,y) dx dy \approx P(x \le X \le x+dx, y \le Y \le y+dy)$$

Interpretation is that

$$P(X \in A, Y \in B) = \int_A \int_B f(x,y) dy dx$$

Property: if X,Y have joint density f(x,y) then X has density

$$f_X(x) = \int_y f(x,y) dy$$

Sums for discrete rvs are replaced by integrals.