Postscript version of this file

STAT 380 Lecture 6

Reading for Today's Lecture: Chapter 3

Goals of Today's Lecture:

• Use first step analysis.

Conditional Expectations

Example:

$$f(x,y) = \begin{cases}x+y & 0 \le x,y \le 1 \\ 0 & \text{otherwise} \end{cases}$$

has conditional of Y|X:

$$f_{Y\vert X}(y\vert x) = \begin{cases} \frac{x+y}{x+\frac{1}{... ...\le x \le 1, y < 0 \\ \text{undefined} & otherwise \end{cases}$$

so, for $0 \le x \le 1$,
$$\begin{align*}{\rm E}(Y\vert X=x) & = \int_0^1 y \frac{x+y}{x+\frac{1}{2}} dy \\ & = \frac{x/2 +1/3}{x+1/2} \end{align*}$$

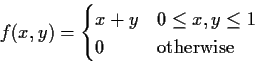
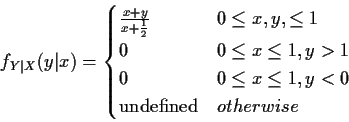
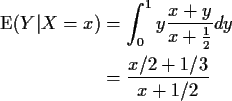
Computing expectations by conditioning:

Notation: ${\rm E}(Y\vert X)$ is the function of X you get by working out ${\rm E}(Y\vert X=x)$, getting a formula in x and replacing x by X. This makes ${\rm E}(Y\vert X)$ a random variable.

Properties:

1: ${\rm E}(A(X)Y+B(X)Z\vert X) = A(X){\rm E}(Y\vert X) +B(X){\rm E}(Z\vert X)$.

2: If Y and X are independent then

$${\rm E}(Y\vert X) = {\rm E}(Y)$$

3: ${\rm E}(1\vert X) = 1$.

4: ${\rm E}\left[{\rm E}(Y\vert X)\right] = {\rm E}(Y)$ (compute average holding X fixed first, then average over X).

In example:

$${\rm E}(Y\vert X) = \frac{X+2/3}{2X+1}$$

Application to last names problem. Put $m={\rm E}(X)$

$$\begin{align*}{\rm E}(Z_n) & = {\rm E}\left[{\rm E}(Z_n\vert X)\right] \\ & = {... ...Z_{n-2}) \\ & \quad \vdots \\ & = m^{n-1}{\rm E}(Z_1) \\ & = m^n \end{align*}$$

For m < 1 expect exponential decay. For m>1 exponential growth (if not extinction).