


Postscript version of this file
STAT 380 Lecture 7
Reading for Today's Lecture: Chapter 4 sections 1-3.
Goals of Today's Lecture:
- Define Markov Chain.
- Introduce transition matrix
- Derive Chapman Kolmogorov equations.
Today's notes
Summary of Probability Review
We have reviewed the following definitions:
- Probability Space (or Sample Space):
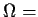 set
of possible outcomes,
set
of possible outcomes, 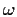 .
.
- Events, subsets of
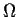 .
.
- Probability: P function defined for events, values in
[0,1] satisfying:
- 1.
-
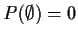 and
and
 .
.
- 2.
- Countable additivity:
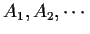 pairwise disjoint
(
pairwise disjoint
(
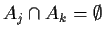 )
)
- Joint, marginal, cond'l prob mass functions: X,Ydiscrete:
- Joint, marginal, conditional densities: X,Y continuous:
- Expected value:
or
- Conditional expectation
or
-
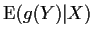 is previous with x replaced by X after getting
formula.
is previous with x replaced by X after getting
formula.
Tactics:
- Convert English expressions to set notation:
- ``Or'' means union (remember inclusive or).
- ``And'' means intersection.
- ``not'' means complement.
- Compute prob something happens as 1-prob it doesn't.
- Break up event into disjoint pieces and add up probabilities.
- Find independent events and write event as intersection.
- Find A, B for which P(A|B) is known.
- Use Bayes rule: if
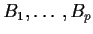 is a partition
then
is a partition
then
- Use first step analysis. (See family names example, craps game,
alternating dice tossing on asst 1.)
Tactics for expected values:
- Use linearity:
- Condition on another variable and use
- Use first step analysis. (Special case of previous.)
Markov Chains
The last names example has the following structure: if, at generation
n there are m individuals then the number of sons in the
next generation has the distribution of the sum of m independent
copies of the random variable X which is the number of sons I have.
This distribution does not depend on n, only on the value m of Zn.
We call Zn a Markov Chain.
Ingredients of a Markov Chain:
- A state space S. S will be finite or countable
in this course.
- A sequence
 of random variables whose values
are all in S.
of random variables whose values
are all in S.
- A matrix
 with entries Pi,j for
with entries Pi,j for 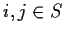 .
The matrix
is required to be stochastic which means
.
The matrix
is required to be stochastic which means
for all i.
The stochastic process
 is called a
Markov chain if
is called a
Markov chain if
for all
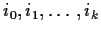 and all k.
and all k.
The matrix  is called a transition matrix.
is called a transition matrix.
Example: If X in the last names example has
a Poisson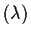 distribution then given Zn=k,
Zn+1 is like the sum of k independent Poisson
distribution then given Zn=k,
Zn+1 is like the sum of k independent Poisson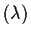 random variables which has a Poisson(
random variables which has a Poisson(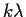 )
distribution.
So
)
distribution.
So
Example: Weather: each day is dry (D) or wet (W).
Xn is weather on day n.
Suppose dry days tend to be followed by dry days, say
3 times in 5 and wet days by wet 4 times in 5.
Markov assumption: yesterday's weather irrelevant to
prediction of tomorrow's given today's.
Transition Matrix:
Now suppose it is wet today. P(wet in 2 days) ?
Notice that all the entries in the last line are items in  .
.
Look at the matrix product
 :
:
Notice that the probability
P(X2=W|X0=W) is exactly the formula for the W,W entry
in
 .
.



Richard Lockhart
2000-10-02
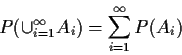


![]() is called a
Markov chain if
is called a
Markov chain if
![]() is called a transition matrix.
is called a transition matrix.
![]() distribution then given Zn=k,
Zn+1 is like the sum of k independent Poisson
distribution then given Zn=k,
Zn+1 is like the sum of k independent Poisson![]() random variables which has a Poisson(
random variables which has a Poisson(![]() )
distribution.
So
)
distribution.
So
![\begin{displaymath}{\bf P}= \left[\begin{array}{llll}
1 & 0 & 0 & \cdots
\\
e^{...
...ts
\\
\vdots &
\vdots &
\vdots &
\ddots
\end{array}\right]
\end{displaymath}](img31.gif)
![\begin{displaymath}{\bf P}= \left[\begin{array}{cc} \frac{3}{5} & \frac{2}{5}
\\
\frac{1}{5} & \frac{4}{5}
\end{array} \right]
\end{displaymath}](img32.gif)
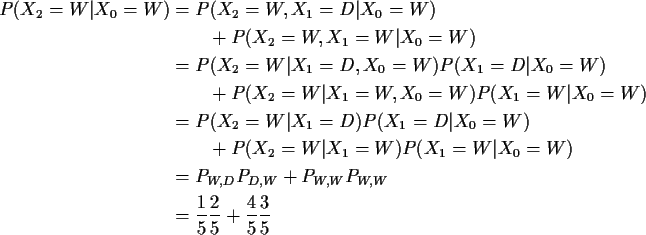
![]() .
.
![]() :
:
![\begin{displaymath}\left[\begin{array}{ll} \frac{3}{5} & \frac{2}{5}
\\
\frac{1...
... \frac{2}{5}
\\
\frac{1}{5} & \frac{4}{5}
\end{array} \right]
\end{displaymath}](img35.gif)