Postscript version of this file

STAT 380 Week 3

Markov Chains

Last names example has following structure: if, at generation $n$ there are $m$ individuals then the number of sons in the next generation has the distribution of the sum of $m$ independent copies of the random variable $X$ which is the number of sons I have. This distribution does not depend on $n$, only on the value $m$ of $Z_n$. We call $Z_n$ a Markov Chain.

Ingredients of a Markov Chain:

• A state space $S$. $S$ will be finite or countable in this course.

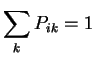• A sequence $X_0,X_1,\ldots$ of random variables whose values are all in $S$.

• Matrix ${\bf P}$ with entries $P_{i,j}$ for $i,j\in S$. ${\bf P}$ is required to be stochastic:
  $$\sum_k P_{ik} = 1$$   and$$\qquad 0 \le P_{ij}$$
  for all $i,j$.

The stochastic process $X_0,X_1,\ldots$ is called a Markov chain if

$$P\left(X_{k+1} =j\vert X_k=i,A\right) = P_{i,j}$$

for any $A$ defined in terms of $X_0,\ldots,X_{k-1}$ and for all $i,j,k$. Usually used with

$$A=\{X_{k-1}=i_{k-1},\ldots,X_0=i_0\}$$

for some $i_0,\ldots,i_{k-1}$.

The matrix ${\bf P}$ is called a transition matrix.

Example: If $X$ in the last names example has a Poisson$(\lambda)$ distribution then given $Z_n=k$, $Z_{n+1}$ is like sum of $k$ independent Poisson$(\lambda)$ rvs which has a Poisson($k\lambda$) distribution. So

$${\bf P}= \left[\begin{array}{llll} 1 & 0 & 0 & \cdots \\ e^{-\l... ...\lambda} & \cdots \\ \vdots & \vdots & \vdots & \ddots \end{array}\right]$$

Example: Weather: each day is dry (D) or wet (W).

$X_n$ is weather on day n.

Suppose dry days tend to be followed by dry days, say 3 times in 5 and wet days by wet 4 times in 5.

Markov assumption: yesterday's weather irrelevant to prediction of tomorrow's given today's.

Transition Matrix:

$${\bf P}= \left[\begin{array}{cc} \frac{3}{5} & \frac{2}{5} \\ \\ \frac{1}{5} & \frac{4}{5} \end{array} \right]$$

Now suppose it's wet today. P(wet in 2 days)?

$$P(X_2=W\vert X_0=W) \hspace*{230pt}$$

$$= P(X_2=W,X_1=D \vert X_0=W)$$

$$\quad + P(X_2=W,X_1=W \vert X_0=W)$$

$$= P(X_2=W\vert X_1=D, X_0=W)$$

$$\qquad \times P(X_1=D\vert X_0=W)$$

$$\quad + P(X_2=W\vert X_1=W ,X_0=W)$$

$$\qquad \times P(X_1=W\vert X_0=W)$$

$$= P(X_2=W \vert X_1=D)$$

$$\qquad \times P(X_1=D\vert X_0=W)$$

$$\quad + P(X_2=W\vert X_1=W)$$

$$\qquad \times P(X_1=W\vert X_0=W)$$

$$= P_{W,D} P_{D,W} +P_{W,W} P_{W,W}$$

$$= \left(\frac{1}{5}\right)\left(\frac{2}{5}\right) + \left(\frac{4}{5}\right)\left(\frac{4}{5}\right)$$

Notice that all the entries in the last line are items in ${\bf P}$. Look at the matrix product ${\bf P}{\bf P}$:

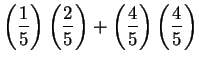$$\left[\begin{array}{ll} \frac{3}{5} & \frac{2}{5} \\ \\ \frac... ...25} & \frac{14}{25} \\ \\ \frac{7}{25} & \frac{18}{25} \end{array} \right]$$

Notice that $P(X_2=W\vert X_0=W)$ is exactly the $W,W$ entry in ${\bf P}{\bf P}$.

General case. Define

$$P^{(n)}_{i,j} =P(X_n=j\vert X_0=i)$$

Then

$$P(X_{m+n}=j \vert X_m=i, X_{m-1}=i_{m-1},\ldots)$$

$$= P(X_{m+n}=j\vert X_m=i)$$

$$=P(X_n=j\vert X_0=i)$$

$$= P^{(n)}_{i,j}$$

$$= \left({\bf P}^n\right)_{ij}$$

Proof of these assertions by induction on $m,n$.

Example for $n=2$. Two bits to do:

First suppose $U,V,X,Y$ are discrete variables. Assume

$$P(Y=y\vert X=x, U=u,V=v)$$

$$= P(Y=y\vert X=x)$$

for any $x,y,u,v$. Then I claim

$$P(Y=y \vert X=x,U=u)$$

$$= P(Y=y\vert X=x)$$

In words, if knowing both $U$ and $V$ doesn't change the conditional probability then knowing $U$ alone doesn't change the conditional probability.

Proof of claim:

$$A=\{X=x,U=u\}$$

Then

$$P(Y=y \vert X=x,U=u)$$

$$= \frac{P(Y=y,A)}{P(A)}$$

$$= \frac{\sum_v P(Y=y,A,V=v)}{P(A)}$$

$$= \frac{\sum_v P(Y=y\vert A,V=v)P(A,V=v)}{P(A)}$$

$$= \frac{\sum_v P(Y=y\vert X=x)P(A,V=v)}{P(A)}$$

$$= \frac{ P(Y=y\vert X=x)\sum_vP(A,V=v)}{P(A)}$$

$$= \frac{ P(Y=y\vert X=x)P(A)}{P(A)}$$

$$= P(Y=y\vert X=x)$$

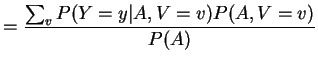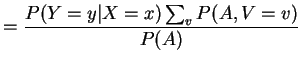Second step: consider

$$P(X_{n+2} =k \vert X_n=i)$$

$$= \sum_j P(X_{n+2}=k,X_{n+1}=j\vert X_n=i)$$

$$= \sum_j P(X_{n+2}=k\vert X_{n+1}=j,X_n=i)$$

$$\qquad \times P(X_{n+1}=j\vert X_n=i)$$

$$= \sum_j P(X_{n+2}=k\vert X_{n+1}=j)$$

$$\qquad \times P(X_{n+1}=j\vert X_n=i)$$

$$= \sum_j {\bf P}_{i,j}{\bf P}_{j,k}$$

This shows that

$$P(X_{n+2}=k\vert X_n=i) = ({\bf P}^2)_{i,k}$$

where ${\bf P}^2$ means the matrix product ${\bf P}{\bf P}$. Notice both that the quantity does not depend on $n$ and that we can compute it by taking a power of ${\bf P}$.

More general version

$$P(X_{n+m}=k\vert X_n=j) = ({\bf P}^m)_{j,k}$$

Since ${\bf P}^n{\bf P}^m={\bf P}^{n+m}$ we get the Chapman-Kolmogorov equations:

$$\begin{multline*} P(X_{n+m}=k\vert X_0=i) = \\ \sum_j P(X_{n+m}=k\vert X_n=j)P(X_n=j\vert X_0=i) \end{multline*}$$

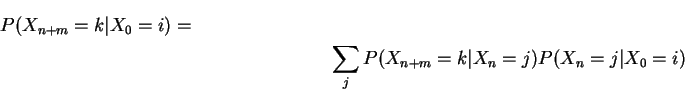
Summary: A Markov Chain has stationary $n$ step transition probabilities which are the $n$th power of the 1 step transition probabilities.

Here is Maple output for the 1,2,4,8 and 16 step transition matrices for our rainfall example:

> p:= matrix(2,2,[[3/5,2/5],[1/5,4/5]]);
                      [3/5    2/5]
                 p := [          ]
                      [1/5    4/5]
> p2:=evalm(p*p):
> p4:=evalm(p2*p2):
> p8:=evalm(p4*p4):
> p16:=evalm(p8*p8):

This computes the powers ( evalm understands matrix algebra).

Fact:

$$\lim_{n\to\infty} {\bf P}^n = \left[ \begin{array}{cc} \frac... ...{2}{3} \\ \\ \frac{1}{3} & \frac{2}{3} \end{array}\right]$$

> evalf(evalm(p));
            [.6000000000    .4000000000]
            [                          ]
            [.2000000000    .8000000000]
> evalf(evalm(p2));
            [.4400000000    .5600000000]
            [                          ]
            [.2800000000    .7200000000]
> evalf(evalm(p4));
            [.3504000000    .6496000000]
            [                          ]
            [.3248000000    .6752000000]
> evalf(evalm(p8));
            [.3337702400    .6662297600]
            [                          ]
            [.3331148800    .6668851200]
> evalf(evalm(p16));
            [.3333336197    .6666663803]
            [                          ]
            [.3333331902    .6666668098]

Where did $1/3$ and $2/3$ come from?

Suppose we toss a coin $P(H)=\alpha_D$ and start the chain with Dry if we get heads and Wet if we get tails.

Then

$$P(X_0=x) = \begin{cases}\alpha_D & x=\text{Dry} \\ \alpha_W=1-\alpha_D & x=\text{Wet} \end{cases}$$

and

$$P(X_1=x) = \sum_y P(X_1=x\vert X_0=y)P(X_0=y)$$

$$= \sum_y \alpha_y P_{y,x}$$

Notice last line is a matrix multiplication of row vector $\alpha$ by matrix ${\bf P}$. A special $\alpha$: if we put $\alpha_D=1/3$ and $\alpha_W=2/3$ then

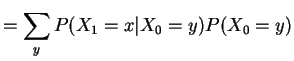$$\left[ \frac{1}{3} \quad \frac{2}{3} \right] \left[\begin{array}{... ...frac{4}{5} \end{array} \right] = \left[ \frac{1}{3} \quad \frac{2}{3} \right]$$

In other words if we start off $P(X_0=D)=1/3$ then $P(X_1=D)=1/3$ and analogously for $W$. This means that $X_0$ and $X_1$ have the same distribution.

A probability vector $\alpha$ is called an initial distribution for the chain if

$$P(X_0=i) = \alpha_i$$

A Markov Chain is stationary if

$$P(X_1=i) = P(X_0=i)$$

for all $i$

An initial distribution is called stationary if the chain is stationary. We find that $\alpha$ is a stationary initial distribution if

$$\alpha {\bf P}=\alpha$$

Suppose ${\bf P}^n$ converges to some matrix ${\bf P}^\infty$. Notice that

$$\lim_{n\to\infty} {\bf P}^{n-1} = {\bf P}^\infty$$

and

$${\bf P}^\infty = \lim {\bf P}^n$$

$$= \left[\lim {\bf P}^{n-1}\right] {\bf P}$$

$$= {\bf P}^\infty {\bf P}$$

This proves that each row $\alpha$ of ${\bf P}^\infty$ satisfies

$$\alpha = \alpha {\bf P}$$

Def'n: A row vector $x$ is a left eigenvector of $A$ with eigenvalue $\lambda$ if

$$xA=\lambda x$$

So each row of ${\bf P}^\infty$ is a left eigenvector of ${\bf P}$ with eigenvalue $1$.