Finding stationary initial distributions. Consider the ![]() for the weather example. The equation
for the weather example. The equation
![$\displaystyle {\bf P}= \left[\begin{array}{cccc}
0 & 1/3 & 0 & 2/3
\\
1/3&0 & 2/3 & 0
\\
0 & 2/3 & 0 & 1/3
\\
2/3 & 0 & 1/3 & 0
\end{array}\right]
$](img12.gif)
p:=matrix([[0,1/3,0,2/3],[1/3,0,2/3,0],
[0,2/3,0,1/3],[2/3,0,1/3,0]]);
[ 0 1/3 0 2/3]
[ ]
[1/3 0 2/3 0 ]
p := [ ]
[ 0 2/3 0 1/3]
[ ]
[2/3 0 1/3 0 ]
> p2:=evalm(p*p);
[5/9 0 4/9 0 ]
[ ]
[ 0 5/9 0 4/9]
p2:= [ ]
[4/9 0 5/9 0 ]
[ ]
[ 0 4/9 0 5/9]
> p4:=evalm(p2*p2):
> p8:=evalm(p4*p4):
> p16:=evalm(p8*p8):
> p17:=evalm(p8*p8*p):
> evalf(evalm(p16));
[.5000000116 , 0 , .4999999884 , 0]
[ ]
[0 , .5000000116 , 0 , .4999999884]
[ ]
[.4999999884 , 0 , .5000000116 , 0]
[ ]
[0 , .4999999884 , 0 , .5000000116]
> evalf(evalm(p17));
[0 , .4999999961 , 0 , .5000000039]
[ ]
[.4999999961 , 0 , .5000000039 , 0]
[ ]
[0 , .5000000039 , 0 , .4999999961]
[ ]
[.5000000039 , 0 , .4999999961 , 0]
> evalf(evalm((p16+p17)/2));
[.2500, .2500, .2500, .2500]
[ ]
[.2500, .2500, .2500, .2500]
[ ]
[.2500, .2500, .2500, .2500]
[ ]
[.2500, .2500, .2500, .2500]
![$\displaystyle p = \left[\begin{array}{cccc}
\frac{2}{5} & \frac{3}{5}
& 0 &0
\\...
...ac{2}{5} & \frac{3}{5}
\\
0 &0 &
\frac{1}{5} & \frac{4}{5}\end{array}\right]
$](img28.gif)
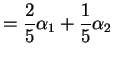 |
||
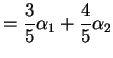 |
||
 |
||
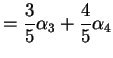 |
||
Pick ![]() in
in ![]() ;
put
;
put
![]() .
.
> p:=matrix([[2/5,3/5,0,0],[1/5,4/5,0,0],
[0,0,2/5,3/5],[0,0,1/5,4/5]]);
[2/5 3/5 0 0 ]
[ ]
[1/5 4/5 0 0 ]
p := [ ]
[ 0 0 2/5 3/5]
[ ]
[ 0 0 1/5 4/5]
> p2:=evalm(p*p):
> p4:=evalm(p2*p2):
> p8:=evalm(p4*p4):
> evalf(evalm(p8*p8));
[.2500000000 , .7500000000 , 0 , 0]
[ ]
[.2500000000 , .7500000000 , 0 , 0]
[ ]
[0 , 0 , .2500000000 , .7500000000]
[ ]
[0 , 0 , .2500000000 , .7500000000]
Notice that rows converge but to two different vectors:
> p:=matrix([[2/5,3/5,0],[1/5,4/5,0],
[1/2,0,1/2]]);
[2/5 3/5 0 ]
[ ]
p := [1/5 4/5 0 ]
[ ]
[1/2 0 1/2]
> p2:=evalm(p*p):
> p4:=evalm(p2*p2):
> p8:=evalm(p4*p4):
> evalf(evalm(p8*p8));
[.2500000000 .7500000000 0 ]
[ ]
[.2500000000 .7500000000 0 ]
[ ]
[.2500152588 .7499694824 .00001525878906]
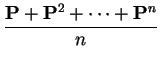
Basic distinguishing features: pattern of 0s in matrix ![]() .
.
State ![]() leads to state
leads to state ![]() if
if
![]() for some
for some ![]() .
It is convenient to agree that
.
It is convenient to agree that
![]() the identity matrix;
thus
the identity matrix;
thus ![]() leads to
leads to ![]() .
.
Note ![]() leads to
leads to ![]() and
and ![]() leads to
leads to ![]() implies
implies ![]() leads to
leads to ![]() (Chapman-Kolmogorov).
(Chapman-Kolmogorov).
States ![]() and
and ![]() communicate if
communicate if ![]() leads to
leads to ![]() and
and ![]() leads
to
leads
to ![]() .
.
The relation of communication is an equivalence relation; it
is reflexive, symmetric and transitive: if
![]() and
and ![]() communicate and
communicate and ![]() and
and ![]() communicate then
communicate then ![]() and
and ![]() communicate.
communicate.
Example (![]() signs indicate non-zero entries):
signs indicate non-zero entries):
![$\displaystyle {\bf P}= \left[\begin{array}{ccccc}
0& 1 & 0 & 0 &0
\\
0 & 0 & ...
...+ & + & 0 & 0
\\
+ & 0 & 0 & + & 0
\\
0 & + & 0 & + & +
\end{array}\right]
$](img55.gif)
For this example:
![]() ,
,
![]() ,
,
![]() so
so ![]() are all in the same communicating class.
are all in the same communicating class.
![]() but not vice versa.
but not vice versa.
![]() but not vice versa.
but not vice versa.
So the communicating classes are
A Markov Chain is irreducible if there is only one communicating class.
Notation:
State ![]() is recurrent if
is recurrent if ![]() , otherwise
transient.
, otherwise
transient.
If ![]() then Markov property (chain starts over when
it gets back to
then Markov property (chain starts over when
it gets back to ![]() ) means prob return infinitely many times
(given started in
) means prob return infinitely many times
(given started in ![]() or given ever get to
or given ever get to ![]() ) is 1.
) is 1.
Consider chain started from transient ![]() .
Let
.
Let ![]() be number of visits
to state
be number of visits
to state ![]() (including visit at time 0). To return
(including visit at time 0). To return ![]() times must return once
then starting over return
times must return once
then starting over return ![]() times, then never return.
So:
times, then never return.
So:
![]() has a Geometric distribution and
has a Geometric distribution and
![]() .
.
Another calculation:
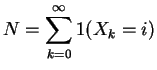
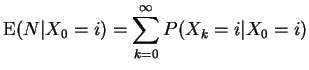


For last example: ![]() and
and ![]() are transient. Claim:
states 1, 2 and 3 are recurrent.
are transient. Claim:
states 1, 2 and 3 are recurrent.
Proof: argument above shows each transient state is visited only finitely many times. So: there is a recurrent state. (Note use of finite number of states.) It must be one of 1, 2 and 3. Proposition: If one state in a communicating class is recurrent then all states in the communicating class are recurrent.
Proof: Let ![]() be the known recurrent state so
be the known recurrent state so
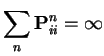

Proposition also means that if 1 state in a class is transient so are all.
State ![]() has period
has period ![]() if
if ![]() is greatest common
divisor of
is greatest common
divisor of
![$\displaystyle {\bf P}= \left[\begin{array}{ccccc}
0& 1 & 0 & 0 &0
\\
0 & 0 & ...
...0 & 0 & 0 & 0
\\
0 & 0 & 0 & 0 & 1
\\
0 & 0 & 0 & 1 & 0
\end{array}\right]
$](img87.gif)
![$\displaystyle {\bf P}= \left[\begin{array}{ccc}
0& 1/2 & 1/2
\\
1 & 0 & 0
\\
1 & 0 & 0
\end{array}\right]
$](img90.gif)
A chain is aperiodic if all its states are aperiodic.