Example: consider a sequence of independent coin tosses with probability ![]() of Heads on a single toss. Let
of Heads on a single toss. Let ![]() be number of heads minus number of tails
after
be number of heads minus number of tails
after ![]() tosses. Put
tosses. Put ![]() .
.
![]() is a Markov Chain. State space is
is a Markov Chain. State space is
![]() , the integers and
, the integers and
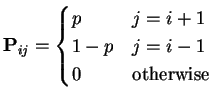
This chain has one communicating class (for ![]() ) and
all states have period 2. According to the strong law of large
numbers
) and
all states have period 2. According to the strong law of large
numbers ![]() converges to
converges to ![]() . If
. If ![]() this guarantees
that for all large enough
this guarantees
that for all large enough ![]()
![]() , that is, the number
of returns to 0 is not infinite. The state 0 is then transient
and so all states must be transient.
, that is, the number
of returns to 0 is not infinite. The state 0 is then transient
and so all states must be transient.
For ![]() the situation is different. It is a fact that
the situation is different. It is a fact that
Local Central Limit Theorem (normal approximation to
![]() ) (or Stirling's approximation) shows
) (or Stirling's approximation) shows

Start irreducible recurrent chain ![]() in state
in state ![]() .
Let
.
Let ![]() be first
be first ![]() such that
such that ![]() .
Define
.
Define
 |
||
 |
||
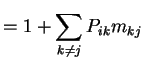 |
Example
![$\displaystyle {\bf P}=
\left[\begin{array}{cc} \frac{3}{5} & \frac{2}{5}
\\
\\
\frac{1}{5} & \frac{4}{5}
\end{array} \right]
$](img30.gif)
 |
||
 |
||
 |
||
 |
Notice stationary initial distribution is



Heuristic: start chain in ![]() . Expect to return to
. Expect to return to ![]() every
every
![]() time units. So are in state
time units. So are in state ![]() about once every
about once every
![]() time units; i.e. limiting fraction of time in state
time units; i.e. limiting fraction of time in state ![]() is
is ![]() .
.
Conclusion: for an irreducible recurrent finite state space Markov chain

Previous conclusion is still right if there is a stationary initial distribution.
Example:
![]() Heads
Heads![]() Tails after
Tails after ![]() tosses
of fair coin. Equations are
tosses
of fair coin. Equations are
 |
||
 |
Some observations:
You have to go through 1 to get to 0 from 2 so
Symmetry (switching H and T):
The transition probabilities are homogeneous:
Conclusion:
 |
||
Summary of the situation:
Every state is recurrent.
All the expected hitting times ![]() are infinite.
are infinite.
All entries
![]() converge to 0.
converge to 0.
Jargon: The states in this chain are null recurrent.
Page 229, question 21: runner goes from front or back
door, prob 1/2 each. Returns front or back, prob 1/2 each.
Has ![]() pairs of shoes, wears pair if any at departure door,
leaves at return door. No shoes? Barefoot. Long run fraction
of time barefoot?
pairs of shoes, wears pair if any at departure door,
leaves at return door. No shoes? Barefoot. Long run fraction
of time barefoot?
Solution: Let ![]() be number of shoes at front door on day
be number of shoes at front door on day ![]() .
Then
.
Then ![]() is a Markov Chain.
is a Markov Chain.
Transition probabilities:
![]() pairs at front door on day
pairs at front door on day ![]() .
. ![]() is
is ![]() if
goes out back door (prob is 1/2) or out front door and back
in front door (prob is 1/4). Otherwise
if
goes out back door (prob is 1/2) or out front door and back
in front door (prob is 1/4). Otherwise ![]() is
is ![]() .
.
![]() pairs at front door on day
pairs at front door on day ![]() .
. ![]() is
is ![]() if out back, in front (prob is 1/4).
if out back, in front (prob is 1/4). ![]() is
is ![]() if out
front, in back. Otherwise
if out
front, in back. Otherwise ![]() is
is ![]() .
.
0 pairs at front door on day ![]() .
. ![]() is 0 if
out front door (prob 1/2) or out back door and in back door
(prob 1/4) otherwise
is 0 if
out front door (prob 1/2) or out back door and in back door
(prob 1/4) otherwise ![]() is
is ![]() .
.
Transition matrix ![]() :
:
![$\displaystyle \left[\begin{array}{cccccc}
\frac{3}{4} & \frac{1}{4} & 0 & 0 &\c...
... \vdots
\\
0 & 0 & 0 & \cdots & \frac{1}{4} & \frac{3}{4}
\end{array}\right]
$](img75.gif)
Doubly stochastic: row sums and column sums are 1.
So
![]() for all
for all ![]() is stationary initial distribution.
is stationary initial distribution.
Solution to problem: 1 day in ![]() no shoes at front door. Half of
those go barefoot. Also 1 day in
no shoes at front door. Half of
those go barefoot. Also 1 day in ![]() all shoes at front door; go
barefoot half of these days. Overall go barefoot
all shoes at front door; go
barefoot half of these days. Overall go barefoot ![]() of the time.
of the time.
Insurance company's reserves fluctuate: sometimes up, sometimes down.
Ruin is event they hit 0 (company goes bankrupt). General problem.
For given model of fluctuation compute probability of ruin either
eventually or in next ![]() time units.
time units.
Simplest model: gambling on Red at Casino. Bet $1 at a time. Win
$1 with probability ![]() , lose $1 with probability
, lose $1 with probability ![]() . Start with
. Start with
![]() dollars. Quit playing
when down to $0 or up to
dollars. Quit playing
when down to $0 or up to ![]() . Compute
. Compute
![]() = fortune after
= fortune after ![]() plays.
plays. ![]() .
.
Transition matrix:
![$\displaystyle {\bf P}=
\left[\begin{array}{cccccc}
1 & 0 & 0 & 0 &\cdots & 0
\...
... & \ddots & \ddots & \vdots
\\
0 & 0 & 0 & \cdots & 0 & 1
\end{array}\right]
$](img84.gif)
Middle equation is
 |
||
 |
||
 |
||
 |

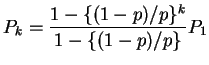
For ![]() we get
we get


Notice that if ![]() our formulas for the sum of the geometric series
are wrong. But for
our formulas for the sum of the geometric series
are wrong. But for ![]() we get
we get
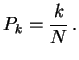
![$\displaystyle {\bf P}= \left[\begin{array}{cccc}
\frac{1}{2} & \frac{1}{2} & 0 ...
...\\
\frac{1}{4} & \frac{1}{4} & \frac{3}{8} & \frac{1}{8}
\end{array}\right]
$](img107.gif)
For ![]() or
or ![]() and
and ![]() or 4:
or 4:
For ![]() or
or ![]()
For
![]() first step analysis:
first step analysis:
 |
||
 |
||
 |
||
 |
In matrix form
![$\displaystyle \left[\begin{array}{cc} m_{3,3} &m_{3,4} \\ \\ m_{4,3} &m_{4,4}\end{array}\right]$](img125.gif) |
![$\displaystyle = \left[\begin{array}{cc} 1 & 0 \\ \\ 0 & 1 \end{array}\right] +$](img126.gif) |
|
![$\displaystyle \qquad \left[\begin{array}{cc} \frac{1}{4} & \frac{1}{4} \\ \\ \f...
...eft[\begin{array}{cc} m_{3,3} &m_{3,4} \\ \\ m_{4,3} &m_{4,4}\end{array}\right]$](img127.gif) |
Translate to matrix notation:
Solution is
![$\displaystyle {\bf I} - {\bf P}_T =
\left[\begin{array}{rr} \frac{3}{4} & -\frac{1}{4} \\ \\
-\frac{3}{8} & \frac{7}{8}
\end{array}\right]
$](img133.gif)
![$\displaystyle {\bf M} = \left[\begin{array}{rr} \frac{14}{9} & \frac{4}{9} \\ \\
\frac{2}{3} & \frac{4}{3}
\end{array}\right]
$](img134.gif)