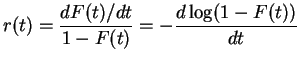Particles arriving over time at a particle detector. Several ways to describe most common model.
Approach 1: numbers of particles arriving in an interval has Poisson distribution, mean proportional to length of interval, numbers in several non-overlapping intervals independent.
For ![]() , denote number of arrivals in
, denote number of arrivals in ![]() by
by ![]() . Model is
. Model is
Approach 2:
Let
![]() be the times at which the particles
arrive.
be the times at which the particles
arrive.
Let
![]() with
with ![]() by convention.
by convention.
Then
![]() are independent Exponential random variables with mean
are independent Exponential random variables with mean ![]() .
.
Note
![]() is called survival function of
is called survival function of ![]() .
.
Approaches are equivalent. Both are deductions of a model based on local behaviour of process.
Approach 3: Assume:
All 3 approaches are equivalent. I show: 3 implies 1, 1 implies 2
and 2 implies 3. First explain ![]() ,
, ![]() .
.
Notation: given functions ![]() and
and ![]() we write
we write

[Aside: if there is a constant ![]() such that
such that

Model 3 implies 1:
Fix ![]() , define
, define ![]() to be conditional probability of 0 points in
to be conditional probability of 0 points in
![]() given value of process on
given value of process on ![]() .
.
Derive differential equation for
![]() . Given process on
. Given process on ![]() and 0 points in
and 0 points in ![]() probability of no
points in
probability of no
points in ![]() is
is


Notice: survival function of exponential rv..
General case. Notation:
![]() .
.
![]() is a non-decreasing function of
is a non-decreasing function of ![]() . Let
. Let
Given ![]() probability that
probability that
![]() is conditional
probability of
is conditional
probability of ![]() points in
points in ![]() .
.
So, for ![]() :
:

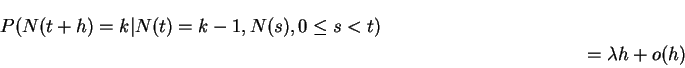

![]() is increasing so only consider
is increasing so only consider ![]() .
.
 |
||
With ![]() we get
we get
Similar ideas permit proof of

If ![]() is a Poisson Process we define
is a Poisson Process we define
![]() to be the times between 0 and the first point, the first point and
the second and so on.
to be the times between 0 and the first point, the first point and
the second and so on.
Fact:
![]() are iid exponential rvs with
mean
are iid exponential rvs with
mean ![]() .
.
We already did ![]() rigorously. The event
rigorously. The event ![]() is exactly the
event
is exactly the
event ![]() . So
. So
I do case of ![]() . Let
. Let ![]() be two positive numbers and
be two positive numbers and
![]() ,
,
![]() . Consider event
. Consider event
This is almost the same as the intersection of the four events:
More rigor:
First step: Compute

Second step: write this in terms of joint cdf of
![]() .
I do
.
I do ![]() :
:

Differentiate twice, that is, take


That completes the first part.
Now compute the joint cdf of ![]() by
by
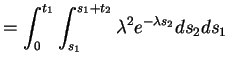 |
||
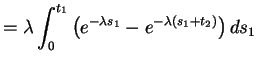 |
||
Summary so far:
Have shown:
Instantaneous rates model implies independent Poisson increments model implies independent exponential interarrivals.
Next: show independent exponential interarrivals implies the instantaneous rates model.
Suppose
![]() iid exponential rvs with means
iid exponential rvs with means ![]() . Define
. Define
![]() by
by ![]() if and only if
if and only if
Let ![]() be the event
be the event
![]() . We
are to show
. We
are to show
If ![]() is a possible trajectory consistent with
is a possible trajectory consistent with ![]() then
then ![]() has jumps at points
has jumps at points
So given
![]() with
with ![]() we are essentially being given
we are essentially being given
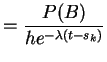 |

The computation of
Convolution: If ![]() and
and ![]() independent rvs with
densities
independent rvs with
densities ![]() and
and ![]() respectively and
respectively and ![]() then
then


If
![]() iid Exponential
iid Exponential![]() then
then
![]() has a Gamma
has a Gamma
![]() distribution. Density
of
distribution. Density
of ![]() is
is
Proof:
 |
Then
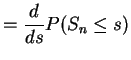 |
||
 |
||
 |
||
 |
||
Extreme Values: If
![]() are independent exponential rvs
with means
are independent exponential rvs
with means
![]() then
then
![]() has an exponential distribution with
mean
has an exponential distribution with
mean
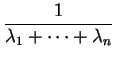
Proof:
 |
Memoryless Property: conditional distribution of
![]() given
given ![]() is
exponential if
is
exponential if ![]() has an exponential distribution.
has an exponential distribution.
Proof:
 |
||
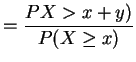 |
||
 |
||
The hazard rate, or instantaneous failure rate for a positive
random variable ![]() with density
with density ![]() and cdf
and cdf ![]() is
is



Weibull random variables have density
Since