
Indications of some proofs:
1)
![]() independent Poisson processes rates
independent Poisson processes rates ![]() ,
,
![]() . Let
. Let ![]() be the event of 2 or more points
in
be the event of 2 or more points
in ![]() in the time interval
in the time interval ![]() ,
, ![]() , the event of exactly
one point in
, the event of exactly
one point in ![]() in the time interval
in the time interval ![]() .
.
Let ![]() and
and ![]() be the corresponding events for
be the corresponding events for ![]() .
.
Let ![]() denote the history of the processes up to time
denote the history of the processes up to time ![]() ; we
condition on
; we
condition on ![]() .
.
We are given:
Note that

Since
Next let ![]() be the event of no points in
be the event of no points in
![]() in the time interval
in the time interval ![]() and
and ![]() the same
for
the same
for ![]() .
Then
.
Then
2) The infinitesimal approach used for 1 can do part of this.
See text for rest. Events defined as in 1):
The event ![]() that there is one point in
that there is one point in ![]() in
in ![]() is the event,
is the event,
![]() that there is exactly one point in any of the
that there is exactly one point in any of the ![]() processes together
with a subset of
processes together
with a subset of ![]() where there are two or more points in
where there are two or more points in ![]() in
in
![]() but exactly one is labeled
but exactly one is labeled ![]() . Since
. Since
![]()
Similarly, ![]() is a subset of
is a subset of ![]() so
so
3) Fix ![]() . Let
. Let ![]() be the number of points
in
be the number of points
in ![]() . Given
. Given ![]() the conditional distribution of
the conditional distribution of
![]() is Binomial
is Binomial![]() with
with
![]() . So
. So
 |
||
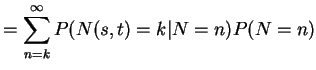 |
||
 |
||
 |
||
 |
||
 |
||
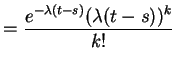 |
4): Fix ![]() for
for
![]() such that
such that

![\begin{multline*}
B \equiv \\
\bigcap_{i=1}^n \{N(s_{i-1}+h_{i-1},s_i]=0,N(s_i,s_i+h_i]=1\}
\\
\cap \{N(s_n+h_n,T]=0\}
\end{multline*}](img84.gif)

 |
||
 |
||
 |
Divide by ![]() and let all
and let all ![]() go to 0 to
get joint density of
go to 0 to
get joint density of
![]() is
is

5) Replace the event ![]() with
with
![]() . With
. With
![]() as before we want
as before we want
![\begin{multline*}
P(A\vert T < S_{n+1}< T+h)
\\
= \frac{ P(B,N(T,T+h] \ge 1)}{P(T < S_{n+1}< T+h)}
\end{multline*}](img94.gif)

We are left to compute the limit of
![$\displaystyle \frac{P(N(T,T+h] \ge 1)}{P(T < S_{n+1}< T+h)}
$](img98.gif)
![\begin{multline*}
\sum_{k=0}^n P(N(0,T]=k,N(T,T+h]=n+1-k)
\\
+o(h) = P(N(0,T]=n)\lambda h+o(h)
\end{multline*}](img99.gif)
![$\displaystyle \frac{P(N(T,T+h] \ge 1)}{P(T < S_{n+1}< T+h)}
$](img98.gif) |
 |
|
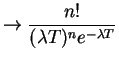 |
The idea of hazard rate can be used to extend the notion of Poisson
Process. Suppose
![]() is a function of
is a function of ![]() . Suppose
. Suppose
![]() is a counting process such that
is a counting process such that

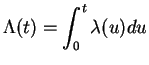
Jargon: ![]() is the intensity or instaneous intensity
and
is the intensity or instaneous intensity
and ![]() the cumulative intensity.
the cumulative intensity.
Can use the model with ![]() any non-decreasing right continuous
function, possibly without a derivative. This allows ties.
any non-decreasing right continuous
function, possibly without a derivative. This allows ties.
Imagine insurance claims arise at times of a Poisson process, ![]() ,
(more likely for an inhomogeneous process).
,
(more likely for an inhomogeneous process).
Let ![]() be the value of the
be the value of the ![]() th claim associated
with the point whose time is
th claim associated
with the point whose time is ![]() .
.
Assume that the ![]() 's are independent of each other and of
's are independent of each other and of
![]() .
.
Let
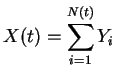
Useful properties: