Consider a population of single celled organisms in a stable environment.
Fix short time interval, length ![]() .
.
Each organism has some probability of dividing to produce two organisms and some other probability of dying.
We might suppose:
Tacit assumptions:
Constants of proportionality do not depend on time: ``stable environment''.
Constants do not depend on organism: organisms are all similar and live in similar environments.
![]() : total population at time
: total population at time ![]() .
.
![]() : history of
process up to time
: history of
process up to time ![]() .
.
Condition on event ![]() .
.
Probability of two or more divisions
(more than one division by a single organism or two or more organisms dividing)
is ![]() .
.
Probability of both a division and a death
or of two or more deaths is ![]() .
.
So probability of exactly 1 division by any one of the ![]() organisms is
organisms is
![]() .
.
Similarly probability of 1 death is
![]() .
.
We deduce:
These equations lead to:
This is the Markov Property.
Definition:A process
![]() taking values in
taking values in
![]() , a finite or countable state space is a Markov Chain
if
, a finite or countable state space is a Markov Chain
if
Definition:A Markov chain ![]() has stationary transitions if
has stationary transitions if
From now on: our chains have stationary transitions.
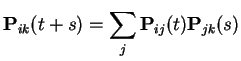








Suppose ![]() a Markov Chain with stationary transitions.
Then
a Markov Chain with stationary transitions.
Then
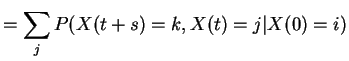 |
||
 |
||
 |
||
 |
||
This shows
Now consider the chain starting from ![]() and let
and let ![]() be
the first
be
the first ![]() for which
for which
![]() . Then
. Then ![]() is
a stopping time.
is
a stopping time.
[Technically:
Conclusion: given ![]() ,
, ![]() has memoryless property
so
has memoryless property
so ![]() has an exponential distribution. Let
has an exponential distribution. Let ![]() be the
rate parameter.
be the
rate parameter.
Let
![]() be the stopping times at which
transitions occur. Then
be the stopping times at which
transitions occur. Then
![]() . The sequence
. The sequence ![]() is a Markov chain by the
Markov property. That
is a Markov chain by the
Markov property. That
![]() reflects the fact
that
reflects the fact
that
![]() by design.
by design.
As before we say
![]() if
if
![]() for some
for some ![]() .
It is fairly clear that
.
It is fairly clear that
![]() for the
for the ![]() if and only
if
if and only
if
![]() for the embedded chain
for the embedded chain ![]() .
.
We say
![]() (
(![]() and
and ![]() communicate) if
communicate) if
![]() and
and
![]() .
.
Now consider
The Chapman-Kolmogorov equations are

The Chapman-Kolmogorov equations can also be written
Look at these equations in component form:

Let ![]() be the matrix with entries
be the matrix with entries

![]() is the infinitesimal generator of the chain.
is the infinitesimal generator of the chain.
Thus
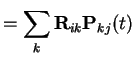 |
||
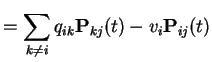 |
On the other hand
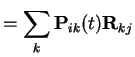 |
||
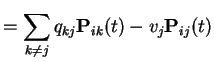 |
Remark: When the state space is infinite the forward equations may not be justified. In deriving them we interchanged a limit with an infinite sum; the interchange is always justified for the backward equations but not for forward.
Example: ![]() . Then
. Then
![$\displaystyle {\bf P}= \left[\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right]
$](img119.gif)
![$\displaystyle {\bf R}= \left[\begin{array}{cc}-v_0 & v_0 \\ v_1 & -v_1 \end{array}\right]
$](img122.gif)
Add ![]() first plus
first plus ![]() third backward equations to get
third backward equations to get

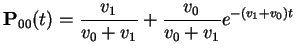
Alternative calculation:
![$\displaystyle {\bf R}= \left[\begin{array}{cc}-v_0 & v_0 \\ v_1 & -v_1 \end{array}\right]
$](img122.gif)
![$\displaystyle {\bf M} = \left[\begin{array}{cc} 1 & v_0\\ \\ 1 & -v_1\end{array}\right]
$](img147.gif)
![$\displaystyle {\bf M}^{-1} = \left[\begin{array}{cc} \frac{v_1}{v_0+v_1} & \frac{v_0}{v_0+v_1}
\\ \\ \frac{1}{v_0+v_1} & \frac{-1}{v_0+v_1}\end{array}\right]
$](img148.gif)
![$\displaystyle {\bf\Lambda} = \left[\begin{array}{cc} 0 & 0\\ \\ 0 & -(v_0+v_1)\end{array}\right]
$](img149.gif)
Then
 |
||
 |
||
 |
![$\displaystyle \sum_0^\infty{\bf\Lambda}^n\frac{t^n}{n!} = \left[\begin{array}{cc}1 & 0 \\ 0&
e^{-(v_0+v_1)t}\end{array}\right]
$](img154.gif)
![$\displaystyle = {\bf M} \left[\begin{array}{cc}1 & 0 \\ 0& e^{-(v_0+v_1)t}\end{array}\right]{\bf M}^{-1}$](img157.gif) |
||
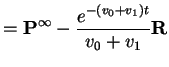 |
![$\displaystyle {\bf P}^\infty=\left[\begin{array}{cc} \frac{v_1}{v_0+v_1} & \fra...
..._0+v_1}
\\
\\
\frac{v_1}{v_0+v_1} & \frac{v_0}{v_0+v_1}
\end{array}\right]
$](img159.gif)
Notice: rows of
![]() are a stationary initial distribution. If rows are
are a stationary initial distribution. If rows are
![]() then
then
![$\displaystyle {\bf P}^\infty = \left[\begin{array}{c}1 \\ 1 \end{array}\right] \pi \equiv {\bf 1}\pi
$](img161.gif)
Fact:
![]() is long run fraction of time in
state 0.
is long run fraction of time in
state 0.
Fact:
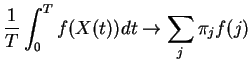
Consider a population of ![]() individuals. Suppose
in next time interval
individuals. Suppose
in next time interval ![]() probability of population
increase of 1 (called a birth) is
probability of population
increase of 1 (called a birth) is
![]() and
probability of decrease of 1 (death) is
and
probability of decrease of 1 (death) is
![]() .
.
Jargon: ![]() is a birth and death process.
is a birth and death process.
Special cases:
All ![]() ; called a pure birth process.
; called a pure birth process.
All
![]() (0 is absorbing): pure death process.
(0 is absorbing): pure death process.
![]() and
and
![]() is a linear
birth and death process.
is a linear
birth and death process.
![]() ,
,
![]() : Poisson Process.
: Poisson Process.
![]() and
and
![]() is a linear
birth and death process with immigration.
is a linear
birth and death process with immigration.
Ingredients of Queuing Problem:
1: Queue input process.
2: Number of servers
3: Queue discipline: first come first serve? last in first out? pre-emptive priorities?
4: Service time distribution.
Example:
Imagine customers arriving at a facility at times of a Poisson
Process ![]() with rate
with rate ![]() . This is the input process,
denoted
. This is the input process,
denoted ![]() (for Markov) in queuing literature.
(for Markov) in queuing literature.
Single server case:
Service distribution: exponential service times, rate ![]() .
.
Queue discipline: first come first serve.
![]() = number of customers in line at time
= number of customers in line at time ![]() .
.
![]() is a Markov process called
is a Markov process called ![]() queue:
queue:

Example:
![]() queue:
queue:
Customers arrive according to PP rate ![]() . Each
customer begins service immediately.
. Each
customer begins service immediately. ![]() is number
being served at time
is number
being served at time ![]() .
. ![]() is a birth and death process
with
is a birth and death process
with

We have seen that a stationary initial distribution ![]() is
a probability vector solving
is
a probability vector solving

So equation says:
Rate of departure from ![]() balances rate of arrival to
balances rate of arrival to ![]() . This is called
balance.
. This is called
balance.
Application to birth and death processes:
Equation is
 |
||
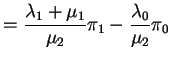 |
||
 |

Apply
![]() to get
to get


If
