Two elementary definitions of expected values:
Defn: If ![]() has density
has density ![]() then
then
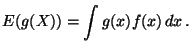
Defn: If ![]() has discrete density
has discrete density ![]() then
then
FACT: If ![]() for a smooth
for a smooth ![]()
 |
||
 |
||
In general, there are random variables which are neither absolutely continuous nor discrete. See STAT 801 for general definition of E.
Defn: We call ![]() integrable if
integrable if
Facts: ![]() is a linear, monotone, positive operator:
is a linear, monotone, positive operator:
Major technical theorems:
Monotone Convergence: If
![]() and
and
![]() (which has to exist) then
(which has to exist) then
Dominated Convergence: If
![]() and
and ![]() rv
rv ![]() such that
such that ![]() (technical
details of this convergence later in the course) and
a random variable
(technical
details of this convergence later in the course) and
a random variable ![]() such that
such that ![]() with
with
![]() then
then
Theorem: With this definition of ![]() if
if ![]() has density
has density
![]() (even in
(even in ![]() say) and
say) and ![]() then
then

Firts conclusion works, e.g., even if ![]() has a density but
has a density but ![]() doesn't.
doesn't.
Defn: The
![]() moment (about the origin) of a real
rv
moment (about the origin) of a real
rv ![]() is
is
![]() (provided it exists).
We generally use
(provided it exists).
We generally use
![]() for
for ![]() .
.
Defn: The
![]() central moment is
central moment is
Defn: For an ![]() valued random vector
valued random vector ![]()
Defn: The (
![]() ) variance covariance matrix of
) variance covariance matrix of ![]() is
is
Moments and probabilities of rare events are closely connected as will be seen in a number of important probability theorems.
Example: Markov's inequality
![$\displaystyle \le E\left[\frac{\vert X-\mu\vert^r}{t^r}1(\vert X-\mu\vert \ge t)\right]$](img48.gif) |
||
![$\displaystyle \le \frac{E[\vert X-\mu\vert^r]}{t^r}$](img49.gif) |
Special Case: Chebyshev's inequality

Example moments: If ![]() is standard normal then
is standard normal then
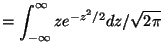 |
||
 |
||
 |
||
 |
||
 |


If now
![]() , that is,
, that is,
![]() ,
then
,
then
![]() and
and
Similarly for
![]() we have
we have ![]() with
with
![]() and
and
Theorem: If
![]() are independent and each
are independent and each ![]() is
integrable then
is
integrable then
![]() is integrable and
is integrable and