Def'n: The moment generating function of a real valued ![]() is
is
Def'n: The moment generating function of ![]() is
is
Formal connection to moments:
![$\displaystyle = \sum_{k=0}^\infty E[(tX)^k]/k!$](img8.gif) |
||
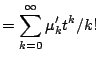 |
Example: : ![]() has density
has density
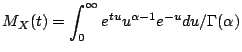
Have power series expansion
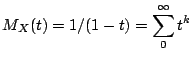
Theorem: If ![]() is finite for all
is finite for all
![]() for some
for some
![]() then
then
Note: ![]() means has continuous derivatives of all orders. Analytic
means has convergent power series expansion in neighbourhood of each
means has continuous derivatives of all orders. Analytic
means has convergent power series expansion in neighbourhood of each
![]() .
.
Theorem: Suppose ![]() and
and ![]() have mgfs
have mgfs ![]() and
and ![]() which are
finite for all
which are
finite for all
![]() . If
. If
![]() for
all
for
all
![]() then
then ![]() and
and ![]() have the same
distribution.
have the same
distribution.
The proof, and many other facts about mgfs, rely on techniques of complex variables.
If
![]() are independent and
are independent and
![]() then
the moment generating function of
then
the moment generating function of ![]() is the product of those
of the individual
is the product of those
of the individual ![]() :
:
Note: also true for multivariate ![]() .
.
Problem: power series expansion of ![]() not
nice function of expansions of individual
not
nice function of expansions of individual ![]() .
.
Related fact: first 3 moments
(meaning ![]() ,
, ![]() and
and ![]() ) of
) of ![]() are sums of those
of the
are sums of those
of the ![]() :
:
![$\displaystyle E[(Y-E(Y))^4] =
\sum \{E[(X_i-E(X_i))^4] -3E^2[(X_i-E(X_i))^2]\}
+ 3 \left\{\sum E[(X_i-E(X_i))^2]\right\}^2\, .
$](img44.gif)
It is possible, however, to replace the moments by other objects called cumulants which do add up properly.
Theorem: If ![]() and
and ![]() are two random variables such that
are two random variables such that
Example: If
![]() are independent and
are independent and ![]() has a
has a
![]() distribution
then
distribution
then
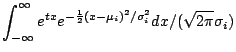 |
||
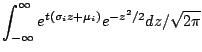 |
||
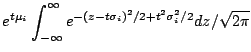 |
||
Example: Suppose that
![]() are independent
are independent
![]() rvs. Then we have defined
rvs. Then we have defined
![]() to have a
to have a ![]() distribution. It is easy to check (see earlier in course)
distribution. It is easy to check (see earlier in course)
![]() has density
has density
Example: The Cauchy density is
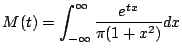
This observation has led to the development of a substitute for the mgf which is defined for every distribution, namely, the characteristic function: