Postscript version of this page

STAT 801: Mathematical Statistics

Confidence Sets

Definition: A level $\beta$ confidence set for a parameter $\phi(\theta)$ is a random subset $C$, of the set of possible values of $\phi$ such that for each $\theta$

$$P_\theta(\phi(\theta) \in C) \ge \beta$$

Confidence sets are very closely connected with hypothesis tests:

From confidence sets to tests

Suppose $C$ is a level $\beta=1-\alpha$ confidence set for $\phi$.

To test $\phi=\phi_0$: reject if $\phi\not\in C$. This test has level $\alpha$.

From tests to confidence sets

Conversely, suppose that for each $\phi_0$ we have available a level $\alpha$ test of $\phi=\phi_0$ who rejection region is say $R_{\phi_0}$.

Define $C=\{\phi_0: \phi=\phi_0$    is not rejected$\}$; get level $1-\alpha$ confidence set for $\phi$.

Example: Usual $t$ test gives rise in this way to the usual $t$ confidence intervals

$$\bar{X} \pm t_{n-1,\alpha/2} \frac{s}{\sqrt{n}}.$$

Confidence sets from Pivots

Definition: A pivot (pivotal quantity) is a function $g(\theta,X)$ whose distribution is the same for all $\theta$. ($\theta$ in pivot is same $\theta$ as being used to calculate distribution of $g(\theta,X)$.

Using pivots to generate confidence sets:

Pick a set $A$ in space of possible values for $g$.

Let $\beta=P_\theta(g(\theta,X) \in A)$; since $g$ is pivotal $\beta$ is the same for all $\theta$.

Given data $X$ solve the relation

$$g(\theta,X) \in A$$

to get

$$\theta \in C(X,A) \, .$$

Example: $(n-1) s^2/\sigma^2 \sim \chi_{n-1}^2$ is a pivot in the $N(\mu,\sigma^2)$ model.

Given $\beta=1-\alpha$ consider the two points

$$\chi_{n-1,1-\alpha/2}^2$$    and $$\chi_{n-1,\alpha/2}^2.$$

Then

$$P(\chi_{n-1,1-\alpha/2}^2 \le (n-1) s^2/\sigma^2 \le \chi_{n-1,\alpha/2}^2) = \beta$$

for all $\mu,\sigma$.

Solve this relation:

$$P( \frac{(n-1)^{1/2} s}{ \chi_{n-1,\alpha/2}} \le \sigma \le \frac{(n-1)^{1/2} s}{ \chi_{n-1,1-\alpha/2}}) = \beta$$

so interval

$$\left[\frac{(n-1)^{1/2} s}{\chi_{n-1,\alpha/2}}, \frac{(n-1)^{1/2} s}{\chi_{n-1,1-\alpha/2}}\right]$$

is a level $1-\alpha$ confidence interval.

In the same model we also have

$$P(\chi_{n-1,1-\alpha}^2 \le (n-1) s^2/\sigma^2 ) = \beta$$

which can be solved to get

$$P(\sigma \le \frac{(n-1)^{1/2} s}{ \chi_{n-1,1-\alpha}}) = \beta$$

This gives a level $1-\alpha$ interval

$$(0,(n-1)^{1/2} s/\chi_{n-1,1-\alpha}) \, .$$

The right hand end of this interval is usually called a confidence upper bound.

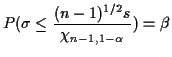
In general the interval from

$$(n-1)^{1/2} s/\chi_{n-1,\alpha_1}$$    to $$(n-1)^{1/2} s/\chi_{n-1,1-\alpha_2}$$

has level $\beta = 1 -\alpha_1-\alpha_2$. For fixed $\beta$ can minimize length of resulting interval numerically -- rarely used. See homework for an example.