Hypothesis testing: a statistical problem where you must choose,
on the basis of data ![]() , between two alternatives. We formalize this
as the problem of choosing between two hypotheses:
, between two alternatives. We formalize this
as the problem of choosing between two hypotheses:
![]() or
or
![]() where
where
![]() and
and ![]() are a partition of the model
are a partition of the model
![]() . That is
. That is
![]() and
and
![]() .
.
A rule for making the required choice can be described in two ways:
For technical reasons which will come up soon I prefer to use the
second description. However, each ![]() corresponds to a
unique rejection region
corresponds to a
unique rejection region
![]() .
.
Neyman Pearson approach treats two hypotheses asymmetrically.
Hypothesis ![]() referred to as the null hypothesis
(traditionally the hypothesis that some treatment has no effect).
referred to as the null hypothesis
(traditionally the hypothesis that some treatment has no effect).
Definition: The power function of a test ![]() (or the corresponding critical region
(or the corresponding critical region ![]() ) is
) is
Interested in optimality theory, that is,
the problem of finding the best ![]() . A good
. A good ![]() will
evidently have
will
evidently have
![]() small for
small for
![]() and large for
and large for
![]() . There is generally a
trade off which can be made in many ways, however.
. There is generally a
trade off which can be made in many ways, however.
Finding a best test is easiest when the hypotheses are very precise.
Definition: A hypothesis ![]() is simple
if
is simple
if ![]() contains only a single value
contains only a single value ![]() .
.
The simple versus simple testing problem arises when we test
![]() against
against
![]() so that
so that ![]() has only two points in it. This problem is of importance as
a technical tool, not because it is a realistic situation.
has only two points in it. This problem is of importance as
a technical tool, not because it is a realistic situation.
Suppose that the model specifies that if
![]() then
the density of
then
the density of ![]() is
is ![]() and if
and if
![]() then
the density of
then
the density of ![]() is
is ![]() . How should we choose
. How should we choose ![]() ?
To answer the question we begin by studying the problem of
minimizing the total error probability.
?
To answer the question we begin by studying the problem of
minimizing the total error probability.
Type I error: the error made when
![]() but we choose
but we choose ![]() , that is,
, that is,
![]() .
.
Type II error: when
![]() but we choose
but we choose
![]() .
.
The level of a simple versus simple test is
Other error probability denoted ![]() is
is
Minimize
![]() , the total error
probability given by
, the total error
probability given by
![$\displaystyle \int[ \phi(x) f_0(x) +(1-\phi(x))f_1(x)] dx$](img41.gif) |
Problem: choose, for each ![]() , either the value
0 or the value 1, in such a way as to minimize the integral.
But for each
, either the value
0 or the value 1, in such a way as to minimize the integral.
But for each ![]() the quantity
the quantity
Theorem: For each fixed ![]() the
quantity
the
quantity
![]() is minimized by any
is minimized by any
![]() which has
which has
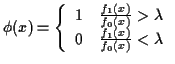
The Neyman and Pearson approach is then to minimize
![]() subject to the constraint
subject to the constraint
![]() .
Usually this is really equivalent to the constraint
.
Usually this is really equivalent to the constraint
![]() (because if you use
(because if you use
![]() you could make
you could make ![]() larger and keep
larger and keep
![]() but
make
but
make ![]() smaller. For discrete models, however, this
may not be possible.
Example: Suppose
smaller. For discrete models, however, this
may not be possible.
Example: Suppose ![]() is Binomial
is Binomial![]() and
either
and
either ![]() or
or ![]() .
.
If ![]() is any critical region
(so
is any critical region
(so ![]() is a subset of
is a subset of
![]() ) then
) then
Possible rejection regions for
![]() :
:
| Region | ||
|
|
0 | 1 |
|
|
0.03125 | |
|
|
0.03125 |
So ![]() minimizes
minimizes ![]() subject to
subject to
![]() .
.
Raise ![]() slightly to 0.0625: possible
rejection regions are
slightly to 0.0625: possible
rejection regions are ![]() ,
, ![]() ,
, ![]() and
and
![]() .
.
The first three have the same ![]() and
and ![]() as before while
as before while ![]() has
has
![]() an
an
![]() . Thus
. Thus ![]() is optimal!
is optimal!
Problem: if all trials are failures ``optimal'' ![]() chooses
chooses
![]() rather than
rather than ![]() . But
. But ![]() makes 5 failures
much more likely does
makes 5 failures
much more likely does ![]() .
.
Problem: discreteness. Here's how we get
around the problem. First we expand the set of possible values of ![]() to include numbers between 0 and 1. Values of
to include numbers between 0 and 1. Values of ![]() between
0 and 1 represent the chance that we choose
between
0 and 1 represent the chance that we choose ![]() given that we observe
given that we observe
![]() ; the idea is that we actually toss a (biased) coin to decide!
This tactic will show us the kinds of rejection regions which are
sensible. In practice we then restrict our attention to levels
; the idea is that we actually toss a (biased) coin to decide!
This tactic will show us the kinds of rejection regions which are
sensible. In practice we then restrict our attention to levels ![]() for which the best
for which the best ![]() is always either 0 or 1. In the
binomial example we will insist that the value of
is always either 0 or 1. In the
binomial example we will insist that the value of ![]() be either 0 or
be either 0 or
![]() or
or
![]() or ...
Smaller example: 4 possible values of
or ...
Smaller example: 4 possible values of ![]() and
and ![]() possible
rejection regions. Here is a table of the levels for each possible rejection region
possible
rejection regions. Here is a table of the levels for each possible rejection region ![]() :
:
| 0 | |
| {3}, {0} | 1/8 |
| {0,3} | 2/8 |
| {1}, {2} | 3/8 |
| {0,1}, {0,2}, {1,3}, {2,3} | 4/8 |
| {0,1,3}, {0,2,3} | 5/8 |
| {1,2} | 6/8 |
| {0,1,3}, {0,2,3} | 7/8 |
| {0,1,2,3} | 1 |
Best level ![]() test has rejection region
test has rejection region
![]() ,
,
![]() .
Best level
.
Best level
![]() test using randomization rejects when
test using randomization rejects when
![]() and, when
and, when ![]() tosses a coin with
tosses a coin with ![]() ,
then rejects if you get H.
Level is
,
then rejects if you get H.
Level is
![]() ; probability of
Type II error is
; probability of
Type II error is
![]() .
.
Definition: A hypothesis test is a function ![]() whose values are always in
whose values are always in ![]() . If we observe
. If we observe ![]() then we
choose
then we
choose ![]() with conditional probability
with conditional probability ![]() .
In this case we have
.
In this case we have
Note that a test using a rejection region ![]() is equivalent to
is equivalent to
The Neyman Pearson Lemma: In testing ![]() against
against ![]() the probability
the probability
![]() of a type II error is minimized, subject to
of a type II error is minimized, subject to
![]() by the test function:
by the test function:
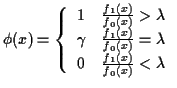
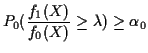
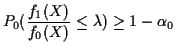
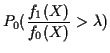 |
|||
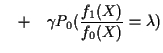 |
|||
Example: Binomial![]() with
with ![]() and
and ![]() :
ratio
:
ratio ![]() is
is
Suppose we have
![]() .
. ![]() must be one
of the possible values of
must be one
of the possible values of ![]() . If we try
. If we try
![]() then
then
Since
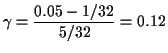
NOTE: No-one ever uses this procedure. Instead the value of ![]() used in discrete problems is chosen to be a possible value of the rejection
probability when
used in discrete problems is chosen to be a possible value of the rejection
probability when ![]() (or
(or ![]() ). When the sample size is large
you can come very close to any desired
). When the sample size is large
you can come very close to any desired ![]() with a non-randomized test.
with a non-randomized test.
If
![]() then we can either take
then we can either take ![]() to be 243/32
and
to be 243/32
and ![]() or
or
![]() and
and ![]() . However, our
definition of
. However, our
definition of ![]() in the theorem makes
in the theorem makes
![]() and
and
![]() .
.
When the theorem is used for continuous distributions it can be the case
that the cdf of
![]() has a flat spot where it is equal to
has a flat spot where it is equal to
![]() . This is the point of the word ``largest'' in the theorem.
. This is the point of the word ``largest'' in the theorem.
Example: If
![]() are iid
are iid ![]() and
we have
and
we have ![]() and
and ![]() then
then
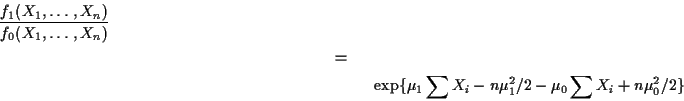
![\begin{multline*}
P_0(\sum X_i > [\log(\lambda) +n\mu_1^2/2]/\mu_1)
\\
=
\\
1-\Phi\left(\frac{\log(\lambda) +n\mu_1^2/2}{n^{1/2}\mu_1}\right)
\end{multline*}](img142.gif)
The rejection region looks complicated: reject if a complicated
statistic is larger than ![]() which has a complicated formula.
But in calculating
which has a complicated formula.
But in calculating ![]() we re-expressed the rejection
region in terms of
we re-expressed the rejection
region in terms of
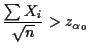
Proof of Neyman Pearson lemma: Given a test ![]() with level strictly less than
with level strictly less than ![]() we can define
the test
we can define
the test
Suppose you want to minimize ![]() subject to
subject to ![]() .
Consider first the function
.
Consider first the function
Notice that to find ![]() you set the usual partial
derivatives equal to 0; then to find the special
you set the usual partial
derivatives equal to 0; then to find the special ![]() you
add in the condition
you
add in the condition
![]() .
.
For each
![]() we have seen that
we have seen that
![]() minimizes
minimizes
![]() where
where
![]() .
.
As ![]() increases the level of
increases the level of
![]() decreases from 1
when
decreases from 1
when ![]() to 0 when
to 0 when
![]() . There is thus a
value
. There is thus a
value ![]() where for
where for
![]() the level is less than
the level is less than
![]() while for
while for
![]() the level is at least
the level is at least ![]() .
Temporarily let
.
Temporarily let
![]() . If
. If
![]() define
define
![]() . If
. If
![]() define
define
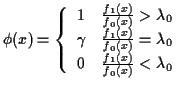
Now ![]() has level
has level ![]() and according to the theorem above
minimizes
and according to the theorem above
minimizes
![]() . Suppose
. Suppose ![]() is some other
test with level
is some other
test with level
![]() . Then
. Then
Example application of NP: Binomial![]() to test
to test ![]() versus
versus
![]() for a
for a ![]() the NP test is of the form
the NP test is of the form
Application of the NP lemma: In the ![]() model
consider
model
consider
![]() and
and
![]() or
or
![]() . The UMP level
. The UMP level ![]() test of
test of
![]() against
against
![]() is
is
Proof: For either choice of ![]() this test has level
this test has level ![]() because
for
because
for ![]() we have
we have
This phenomenon is somewhat general. What happened was this. For
any
![]() the likelihood ratio
the likelihood ratio ![]() is an increasing
function of
is an increasing
function of ![]() . The rejection region of the NP test is thus
always a region of the form
. The rejection region of the NP test is thus
always a region of the form
![]() . The value of the constant
. The value of the constant
![]() is determined by the requirement that the test have level
is determined by the requirement that the test have level ![]() and this depends on
and this depends on ![]() not on
not on ![]() .
.
Definition: The family
![]() has monotone likelihood ratio with respect to a statistic
has monotone likelihood ratio with respect to a statistic ![]() if for each
if for each
![]() the likelihood ratio
the likelihood ratio
![]() is a monotone increasing function of
is a monotone increasing function of ![]() .
.
Theorem: For a monotone likelihood ratio family the
Uniformly Most Powerful level ![]() test of
test of
![]() (or of
(or of
![]() ) against the alternative
) against the alternative
![]() is
is
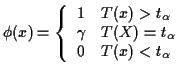
Typical family where this works: one parameter exponential family. Usually there is no UMP test.
Example: test ![]() against two sided alternative
against two sided alternative
![]() . There is no UMP level
. There is no UMP level
![]() test.
test.
If there were its power at ![]() would have to be
as high as that of the one sided level
would have to be
as high as that of the one sided level ![]() test and so its rejection
region would have to be the same as that test, rejecting for large
positive values of
test and so its rejection
region would have to be the same as that test, rejecting for large
positive values of
![]() . But it also has to have power as
good as the one sided test for the alternative
. But it also has to have power as
good as the one sided test for the alternative
![]() and
so would have to reject for large negative values of
and
so would have to reject for large negative values of
![]() .
This would make its level too large.
.
This would make its level too large.
Favourite test: usual 2 sided test rejects for large values
of
![]() .
Test maximizes power subject to two constraints: first,
level
.
Test maximizes power subject to two constraints: first,
level ![]() ; second power is minimized at
; second power is minimized at ![]() .
Second condition means
power on alternative is larger than on the null.
.
Second condition means
power on alternative is larger than on the null.