


Postscript version of this page
STAT 801: Mathematical Statistics
Unbiased Tests
Definition: A test  of
of  against
against
 is unbiased level
is unbiased level  if it has level
if it has level  and,
for every
and,
for every
 we have
we have
When testing a point null hypothesis like 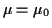 this requires
that the power function be minimized at
this requires
that the power function be minimized at  which will mean that
if
which will mean that
if 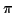 is differentiable then
is differentiable then
Example:  :
data
:
data
 .
If
.
If  is any test function then
is any test function then
Differentiate under the integral and use
to get the condition
Minimize
 subject to
two constraints
subject to
two constraints
and
Fix two
values
 and
and  and minimize
The quantity in question is just
As before this is minimized by
and minimize
The quantity in question is just
As before this is minimized by
The likelihood ratio  is simply
is simply
and this exceeds the linear function
for all  sufficiently large or small. That is,
is minimized by a rejection region of the form
Satisfy constraints: adjust
sufficiently large or small. That is,
is minimized by a rejection region of the form
Satisfy constraints: adjust  and
and  to get
level
to get
level  and
and
 . 2nd condition
shows rejection region symmetric about
. 2nd condition
shows rejection region symmetric about  so
test rejects for
so
test rejects for
Mimic Neyman Pearson lemma proof to check
that if  and
and  are adjusted so that the
unconstrained problem has the rejection region given then the
resulting test minimizes
are adjusted so that the
unconstrained problem has the rejection region given then the
resulting test minimizes  subject to the two constraints.
subject to the two constraints.
A test  is a Uniformly Most Powerful Unbiased level
is a Uniformly Most Powerful Unbiased level  test if
test if
 has level
has level
 .
.
 is unbiased.
is unbiased.
- If
 has level
has level
 and
and  is unbiased
then for every
is unbiased
then for every
 we have
we have
Conclusion: The two sided  test which rejects
if
test which rejects
if
where
is the uniformly most powerful unbiased test of 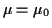 against the two sided alternative
against the two sided alternative
 .
.
Nuisance Parameters
The  -test is UMPU.
-test is UMPU.
Suppose
 iid
iid
 .
Test
.
Test 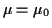 or
or
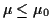 against
against 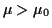 .
Parameter space is two dimensional; boundary
between the null and alternative is
.
Parameter space is two dimensional; boundary
between the null and alternative is
If a test has
 for all
for all
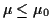 and
and
 for
all
for
all
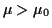 then
then
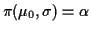 for all
for all  because the power function of any test must
be continuous. (Uses dominated convergence
theorem; power function is an integral.)
because the power function of any test must
be continuous. (Uses dominated convergence
theorem; power function is an integral.)
Think of
 as
parameter space for a model. For this parameter space
as
parameter space for a model. For this parameter space
is complete and sufficient. Remember
definitions of both completeness and sufficiency depend
on the parameter space.
Suppose
 is an unbiased level
is an unbiased level  test. Then we have
test. Then we have
for all  . Condition on
. Condition on  and get
for all
and get
for all  . Sufficiency guarantees that
is a statistic and completeness that
. Sufficiency guarantees that
is a statistic and completeness that
Now let us fix a single value of  and a
and a
 .
To make our notation simpler I take
.
To make our notation simpler I take  .
Our observations above permit us to condition on
.
Our observations above permit us to condition on  . Given
. Given
 we have a level
we have a level  test which is a function of
test which is a function of
 .
.
If we maximize the conditional power of this test for each  then
we will maximize its power. What is the conditional model
given
then
we will maximize its power. What is the conditional model
given  ? That is, what is the conditional distribution of
? That is, what is the conditional distribution of
 given
given  ? The answer is that the joint density of
? The answer is that the joint density of
 is of the form
is of the form
where
 and
and
 .
.
This makes the conditional density of  given
given  of the form
of the form
Note disappearance of  and null is
and null is
 . This permits application of NP lemma
to the conditional family to prove that UMP unbiased test has
form
where
. This permits application of NP lemma
to the conditional family to prove that UMP unbiased test has
form
where  chosen to make conditional level
chosen to make conditional level  .
The function
.
The function
 is increasing in
is increasing in  for
each
for
each  so that we can rewrite
so that we can rewrite  in the form
for some
in the form
for some  . The quantity
is the usual
. The quantity
is the usual  statistic and is exactly independent of
statistic and is exactly independent of  (see Theorem
6.1.5 on page 262 in Casella and Berger). This guarantees that
and makes our UMPU test the usual
(see Theorem
6.1.5 on page 262 in Casella and Berger). This guarantees that
and makes our UMPU test the usual  test.
test.
Optimal tests
- A good test has
 large on the alternative and small on the null.
large on the alternative and small on the null.
- For one sided one parameter families with MLR a UMP test exists.
- For two sided or multiparameter families the best to be hoped for
is UMP Unbiased or Invariant or Similar.
- Good tests are found as follows:
- Use the NP lemma to
determine a good rejection region for a simple alternative.
- Try to express that region in terms of a statistic whose
definition does not depend on the specific alternative.
- If this fails impose an additional criterion such as unbiasedness.
Then mimic the NP lemma and again try to simplify the rejection region.



Richard Lockhart
2001-03-26
![]() of
of ![]() against
against
![]() is unbiased level
is unbiased level ![]() if it has level
if it has level ![]() and,
for every
and,
for every
![]() we have
we have
![]() this requires
that the power function be minimized at
this requires
that the power function be minimized at ![]() which will mean that
if
which will mean that
if ![]() is differentiable then
is differentiable then
![]() :
data
:
data
![]() .
If
.
If ![]() is any test function then
is any test function then



![]() subject to
two constraints
subject to
two constraints
![$\displaystyle \int [\phi(x) f_0(x)(\lambda_1+\lambda_2(\bar{x} - \mu_0)) +
(1-\phi(x))f_1(x)] dx \, .
$](img22.gif)
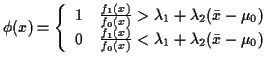
![]() is simply
is simply
![]() and
and ![]() are adjusted so that the
unconstrained problem has the rejection region given then the
resulting test minimizes
are adjusted so that the
unconstrained problem has the rejection region given then the
resulting test minimizes ![]() subject to the two constraints.
subject to the two constraints.
![]() is a Uniformly Most Powerful Unbiased level
is a Uniformly Most Powerful Unbiased level ![]() test if
test if
![]() test which rejects
if
test which rejects
if
![]() -test is UMPU.
-test is UMPU.
![]() iid
iid
![]() .
Test
.
Test ![]() or
or
![]() against
against ![]() .
Parameter space is two dimensional; boundary
between the null and alternative is
.
Parameter space is two dimensional; boundary
between the null and alternative is
![]() for all
for all
![]() and
and
![]() for
all
for
all
![]() then
then
![]() for all
for all ![]() because the power function of any test must
be continuous. (Uses dominated convergence
theorem; power function is an integral.)
because the power function of any test must
be continuous. (Uses dominated convergence
theorem; power function is an integral.)
![]() as
parameter space for a model. For this parameter space
as
parameter space for a model. For this parameter space
![]() is an unbiased level
is an unbiased level ![]() test. Then we have
test. Then we have
![]() and a
and a
![]() .
To make our notation simpler I take
.
To make our notation simpler I take ![]() .
Our observations above permit us to condition on
.
Our observations above permit us to condition on ![]() . Given
. Given
![]() we have a level
we have a level ![]() test which is a function of
test which is a function of
![]() .
.
![]() then
we will maximize its power. What is the conditional model
given
then
we will maximize its power. What is the conditional model
given ![]() ? That is, what is the conditional distribution of
? That is, what is the conditional distribution of
![]() given
given ![]() ? The answer is that the joint density of
? The answer is that the joint density of
![]() is of the form
is of the form
![]() given
given ![]() of the form
of the form
![$\displaystyle T=\frac{n^{1/2}\bar{X}}{\sqrt{n[S/n-\bar{X}^2]/(n-1)}}
$](img79.gif)