Why bother doing the Newton Raphson steps?
Why not just use the method of moments estimates?
Answer: method of moments estimates not usually as close to right answer as MLEs.
Rough principle: A good estimate
![]() of
of ![]() is usually
close to
is usually
close to ![]() if
if ![]() is the true value of
is the true value of ![]() . Closer
estimates, more often, are better estimates.
. Closer
estimates, more often, are better estimates.
This principle must be quantified if we are to ``prove'' that the mle is a good estimate. In the Neyman Pearson spirit we measure average closeness.
Definition: The Mean Squared Error (MSE) of an estimator
![]() is the function
is the function
Standard identity:
Primitive example: I take a coin from my pocket and toss it
6 times. I get ![]() . The MLE of the probability of heads is
. The MLE of the probability of heads is
Alternative estimate:
![]() .
.
That is,
![]() ignores data; guess coin is fair.
ignores data; guess coin is fair.
The MSEs of these two estimators are
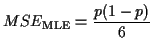
For this reason I would recommend use of ![]() for sample sizes this small.
for sample sizes this small.
Same experiment with a thumbtack: tack can land point up (U) or tipped over (O).
If I get
![]() how should I estimate
how should I estimate ![]() the probability of
the probability of ![]() ?
?
Mathematics is identical to above but is
![]() is better than
is better than ![]() ?
?
Less reason to believe
![]() than
with a coin.
than
with a coin.