Cauchy problem: for vector
![]() we define
we define
![]() to be that root of
to be that root of
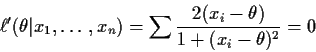
It is possible to prove that this defines a Borel function from
![]() to
to ![]() .
Now define
.
Now define
To prove this fix
![]() we prove that
we prove that
![]() where
where
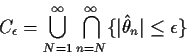
Notation:
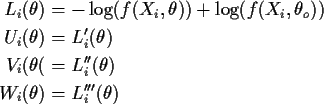
Define
![]() to be the event that there is
an N such that for all
to be the event that there is
an N such that for all ![]() and all
and all
![]() we have
we have
Already shown:
![]() .
.
Next show
![]() .
Note that
.
Note that
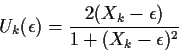
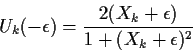
![]() ,
,
![]() averages of
iid variates. Apply SLLN and show
averages of
iid variates. Apply SLLN and show
![]()
In fact
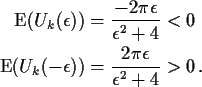
Defect: argument not easy to generalize; uses exact computation of moment.
More general tactic: use Jensen's inequality.
If ![]() is smaller at
is smaller at ![]() and at
and at ![]() than it is
at 0 then there must be a critical point in
than it is
at 0 then there must be a critical point in
![]() ,
that is, a root of
,
that is, a root of
![]() .
.
Define
![]() is the event
is the event ![]() such
that
such
that
![]()
If so then
To prove the claim we apply Jensen's inequality:
Jargon: ![]() is convex if for each x,y and
is convex if for each x,y and
![]()
If ![]() is twice differentiable and
is twice differentiable and
![]() then
then ![]() is convex; a strict inequality shows
is convex; a strict inequality shows ![]() is strictly
convex.
is strictly
convex.
Apply Jensen's inequality with
![]() to
Y=g(X)/f(X) where X has density f and g is some other
density. Then
to
Y=g(X)/f(X) where X has density f and g is some other
density. Then
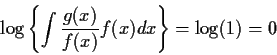
Technically: interval (a,b) is
![]() .
The assumption
.
The assumption
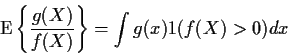
The other technical detail is that g(x) might be 0 some places where
f(x) is not 0. This might mean
P(Y=0) > 0. On the event Y=0we will agree to take
![]() and conclude
and conclude
Applied to our Cauchy problem we have shown
![]() for all
for all
![]() .
Hence
.
Hence
![]() .
.
Finally we consider
![]() .
Up to now we have been
able to make do with an arbitrary
.
Up to now we have been
able to make do with an arbitrary ![]() .
In this case, however,
the result holds only for small
.
In this case, however,
the result holds only for small
![]() .
First consider
.
First consider
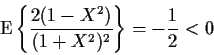
Pick
![]() so that
so that
![]() .
If B is the event
.
If B is the event
This proves that for all
![]()
We have now shown that for
![]()
Consider parametric family
Let
![]() be the event:
be the event: ![]() such that
such that
![]()
![]() has a local maximum on the interval
has a local maximum on the interval
![]() .
.
We have proved quite generally that
| (2) |
Add assumption
| (A) |
| (3) |
The event
![]() then has probability 1. On
this event there is a sequence of roots of the likelihood equations
which is consistent.
then has probability 1. On
this event there is a sequence of roots of the likelihood equations
which is consistent.
Remaining problem: prove, under
general conditions, that there is probably only one root near ![]() .
.
Consider event that
![]() is monotone on
is monotone on
![]() .
Previous proof based on showing
that next derivative was negative at
.
Previous proof based on showing
that next derivative was negative at ![]() and did not
change much over a small enough interval.
and did not
change much over a small enough interval.
Behaviour at ![]() is essentially the behaviour of
is essentially the behaviour of
Begin with
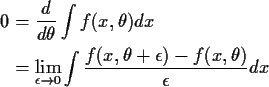
In order to take the limit inside the integral sign we must prove that for
any sequence
![]()

Normally: apply dominated convergence theorem.
If f is continuously differentiable wrt ![]() then
difference quotient is exactly
then
difference quotient is exactly
One tactic: compute
Assuming dominated convergence theorem applies:
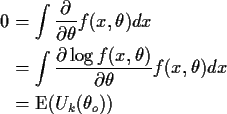
Differentiating again and again passing limits through integrals
gives
Next we consider
Define
Pick ![]() so small that
bound strictly smaller than
so small that
bound strictly smaller than