Postscript version of this file

STAT 870 Lecture 8

Markov Chains

Stochastic process: family $\{X_i;i\in I\}$ of rvs I the index set. Often $I\subset {\Bbb R}$, e.g.  $[0,\infty)$, [0,1]$\Bbb Z$ or $\Bbb N$.

Continuous time: I is an interval

Discrete time: $I\subset {\Bbb Z}$.

Generally all X_n take values in state space S. In following S is a finite or countable set; each X_n is discrete.

Usually S is $\Bbb Z$, $\Bbb N$ or $\{0,\ldots,m\}$ for some finite m.

Markov Chain: stochastic process $X_n;n \in {\Bbb N}$. taking values in a finite or countable set S such that for every n and every event of the form

$$A=\{ (X_0,\ldots,X_{n-1})\in B\subset S^n\}$$

we have

 

P(X_n+1=j|X_n=i,A) = P(X₁=j|X₀=i) (1)

Notation: ${\bf P}$ is the (possibly infinite) array with elements

P_ij = P(X₁=j|X₀=i)

indexed by $i,j \in S$.

${\bf P}$ is the (one step) transition matrix of the Markov Chain.

Conditional Probability: An Aside

If P(A) > 0 we define

$$P(B\vert A) = \frac{P(AB)}{P(A)}$$

In this chapter all random variables are discrete and so when we condition on values of a finite list of variables we will be conditioning on an event of positive probability. If we try to move to continuous state spaces we will have to improve our understanding of conditional probability and expectation.

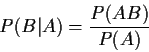
WARNING: in (1) we require the condition to hold only when

P(X_n=i,A) > 0

End of Aside

Evidently the entries in ${\bf P}$ are non-negative and

$$\sum_j P_{ij} =1$$

for all $i\in S$. Any such matrix is called stochastic.

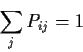
We define powers of ${\bf P}$ by

$$\left({\bf P}^n\right)_{ij} = \sum_k \left({\bf P}^{n-1}\right)_{ik}P_{kj}$$

Notice that even if S is infinite these sums converge absolutely.

Chapman-Kolmogorov Equations

Condition on X_l+n-1 to compute

P(X_l+n=j|X_l=i)

$$\begin{align*}P(&X_{l+n}=j\vert X_l=i) \\ & = \sum_k P(X_{l+n}=j,X_{l+n-1}=k\v... ...k\vert X_l=i) \\ & = \sum_k P(X_{l+n-1}=k\vert X_l=i) {\bf P}_{kj} \end{align*}$$
Now condition on X_l+n-2 to get
$$\begin{multline*}P(X_{l+n}=j\vert X_l=i) = \\ \sum_{k_1k_2} {\bf P}_{k_1k_2}{\bf P}_{k_2j} P(X_{l+n-2}=k_1\vert X_l=i) \end{multline*}$$

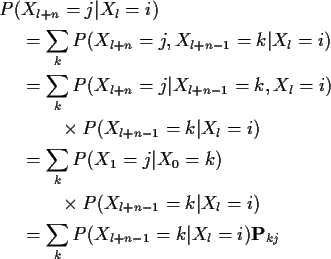
Notice: sum over k₂ computes k₁,j entry in matrix ${\bf P}{\bf P}={\bf P}^2$.
$$\begin{multline*}P(X_{l+n}=j\vert X_l=i) = \\ \sum_{k_1} ({\bf P}^2)_{k_1,j} P(X_{l+n-2}=k_1\vert X_l=i) \end{multline*}$$
We may now prove by induction on n that

$$P(X_{l+n}=j\vert X_l=i)= ({\bf P}^n)_{ij} \, .$$

This proves Chapman-Kolmogorov equations:
$$\begin{align*}P(X_{l+m+n}& = j\vert X_l=i) = \\ & \sum_k P(X_{l+m}=k\vert X_l=i) \\ & \qquad \times P(X_{l+m+n} = j\vert X_{l+m}=k) \end{align*}$$
These are simply a restatement of the identity

$${\bf P}^{n+m} = {\bf P}^n {\bf P}^m \, .$$

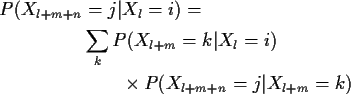
Remark: It is important to notice that these probabilities depend on m and n but not on l. We say the chain has stationary transition probabilities. A more general definition of Markov chain than (1) is
$$\begin{multline*}P(X_{n+1} = j\vert X_n=i, A) \\ = P(X_{n+1} = j\vert X_n=i) \, . \end{multline*}$$
Notice RHS now permitted to depend on n.

Define ${\bf P}^{n,m}$: matrix with i,jth entry

P(X_m=j|X_n=i)

for m>n. Then

$${\bf P}^{r,s}{\bf P}^{s,t} = {\bf P}^{r,t}$$

Also called Chapman-Kolmogorov equations. This chain does not have stationary transitions.

Remark: The calculations above involve sums in which all terms are positive. They therefore apply even if the state space S is countably infinite.

Extensions of the Markov Property

Function $f(x_0,x_1,\ldots)$ defined on $S^\infty$ = all infinite sequences of points in S.

Let B_n be the event

$$f(X_n,X_{n+1},\ldots) \in C$$

for suitable C in range space of f. Then

 

P(B_n|X_n = x, A) = P(B₀|X₀=x) (2)

for any event A of the form

$$\{(X_0,\ldots,X_{n-1}) \in D\}$$

Also

 

P(AB_n|X_n=x) = P(A|X_n=x)P(B_n|X_n=x) (3)

``Given the present the past and future are conditionally independent.''

Proof of (2):

Special case:

$$B_n = \{ (X_{n+1} = x_1 , \cdots, X_{n+m}=x_m\}$$

LHS of (2) evaluated by repeated conditioning (cf. Chapman-Kolmogorov):

$${\bf P}_{x,x_1}{\bf P}_{x_1,x_2} \cdots {\bf P}_{x_{m-1},x_m}$$

Same for RHS.

Events defined from $X_n,\ldots,X_{n+m}$: sum over appropriate vectors $x,x_1,\ldots,x_m$.

General case: montone class techniques.

To prove (3) write
$$\begin{align*}P(AB_n& \vert X_n=x) \\ & = P(B_n\vert X_n=x,A)P(A\vert X_n=x) \\ & = P(B_n\vert X_n=x)P(A\vert X_n=x) \end{align*}$$
using (2).

Classification of States

If an entry ${\bf P}_{ij}$ is 0 it is not possible to go from state ito state j in one step. It may be possible to make the transition in some larger number of steps, however. We say i leads to j(or j is accessible from i) if there is an integer $n \ge 0$ such that

$$P(X_n=j\vert X_0=i) > 0 \, .$$

We use the notation $i \leadsto j$. By defining ${\bf P}^0$ to be the identity matrix ${\bf I}$ we arrive at $i \leadsto j$ if there is an $n \ge 0$ for which $({\bf P}^n)_{ij}> 0$.

We say states i and j communicate if $i \leadsto j$ and $j\leadsto i$. We write $i {\leftrightarrow}j$ if i and j communicate. Communication is an equivalence relation, that is, a reflexive, symmetric and transitive relation on the states of S. More precisely:

Reflexive: for all i we have $i {\leftrightarrow}j$.

Symmetric: if $i {\leftrightarrow}j$ then $j {\leftrightarrow}i$.

Transitive: if $i {\leftrightarrow}j$ and $j{\leftrightarrow}k$ then $i{\leftrightarrow}k$.

Proof:

Reflexive: follows from our inclusion of n=0 in the definition of leads to.

Symmetry is obvious.

Transitivity: suffices to check that $i \leadsto j$ and $j \leadsto k$ imply that $i\leadsto k$. But if $({\bf P}^m)_{ij}>0$ and $({\bf P}^n)_{jk}>0$ then
$$\begin{align*}({\bf P}^{m+n})_{ik}& = \sum_l ({\bf P}^m)_{il} ({\bf P}^n)_{lk} \\ & \ge ({\bf P}^m)_{ij}({\bf P}^n)_{jk} \\ & > 0 \end{align*}$$

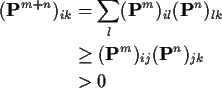
Any equivalence relation on a set partitions the set into equivalence classes; two elements are in the same equivalence class if and only if they are equivalent.

Communication partitions S into equivalence classes called communicating classes.

Example:

$${\bf P}= \left[\begin{array}{cccccccc} \frac{1}{4} & \frac{1}... ... & 0 & 0 &0 &0 & \frac{1}{2} & \frac{1}{2} \end{array}\right]$$

Find communicating classes: start with say state 1, see where it leads.

• $1\leadsto 2$, $1\leadsto 3$ and $1\leadsto 4$ in row 1.

• Row 4: $4\leadsto 1$. So: (transitivity) 1, 2, 3 and 4 all in the same communicating class.

• Claim: none of these leads to 5, 6, 7 or 8.

  Suppose $i\in \{1,2,3,4\}$ and $j\in \{5,6,7,8\}$. Then $({\bf P}^n)_{ij}$ is sum of products of ${\bf P}_{kl}$. Cannot be positive unless there is a sequence $i_0=i,i_1,\ldots,i_n=j$with ${\bf P}_{i_{k-1},i_{k}}>0$ for $k=1,\ldots,n$.

  Consider first k for which $i_k \in \{5,6,7,8\}$ Then $i_{k-1}\in \{1,2,3,4\}$ and so ${\bf P}_{i_{k-1},i_{k}}=0$.

So: $\{1,2,3,4\}$ is a communicating class.

• $5 \leadsto 1$, $5 \leadsto 2$, $5\leadsto 3$ and $5\leadsto 4$.

• None of these lead to any of $\{5,6,7,8\}$ so $\{5\}$ must be communicating class.

• Similarly $\{6\}$ and $\{7,8\}$ are communicating classes.

Note: states 5 and 6 have special property. Each time you are in either state you run a risk of going to one of the states 1, 2, 3 or 4. Eventually you will make such a transition and then never return to state 5 or 6.

States 5 and 6 are transient.

To make this precise define hitting times:

$$T_k= \min\{n>0: X_n=k\}$$

We define

$$f_k = P(T_k < \infty\vert X_0=k)$$

State k is transient if f_k< 1 and recurrent if f_k=1.

Let N_k be number of times chain is ever in state k.

Claims:

1.

If f_i < 1 then N_k has a Geometric distribution:

P(N_k=r|X₀=k) = f_k^r-1(1-f_k)

for $r=1,2,\ldots$.

2.

If f_i=1 then

$$P(N_k=\infty\vert X_0=k) = 1$$

Proof using strong Markov property:

Stopping time for the Markov chain is a random variable T taking values in $\{0, 1,\cdots\}\cup\{\infty\}$ such that for each finite k there is a function f_k such that

$$1(T=k) = f_k(X_0,\ldots,X_k)$$

Notice that T_k in theorem is a stopping time.

Standard shorthand notation: by

P^x(A)

we mean

$$P(A\vert X_0=x) \, .$$

Similarly we define

$${\rm E}^x(Y)= {\rm E}(Y\vert X_0=x) \, .$$