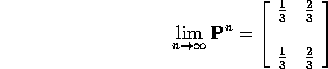
STAT 870 Lecture 11
> p:= matrix(2,2,[[3/5,2/5],[1/5,4/5]]);
[3/5 2/5]
p := [ ]
[1/5 4/5]
> p2:=evalm(p*p):
> p4:=evalm(p2*p2):
> p8:=evalm(p4*p4):
> p16:=evalm(p8*p8):
This computes the powers (evalm understands
matrix algebra).
Fact:
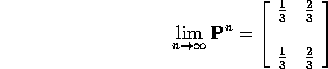
> evalf(evalm(p));
[.6000000000 .4000000000]
[ ]
[.2000000000 .8000000000]
> evalf(evalm(p2));
[.4400000000 .5600000000]
[ ]
[.2800000000 .7200000000]
> evalf(evalm(p4));
[.3504000000 .6496000000]
[ ]
[.3248000000 .6752000000]
> evalf(evalm(p8));
[.3337702400 .6662297600]
[ ]
[.3331148800 .6668851200]
> evalf(evalm(p16));
[.3333336197 .6666663803]
[ ]
[.3333331902 .6666668098]
Where did 1/3 and 2/3 come from?
Suppose we toss a coin 
and start the
chain with Dry if we get heads and Wet if we get
tails.
Then
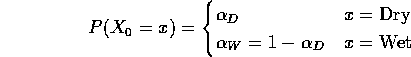
and
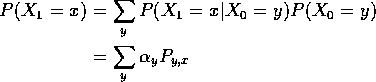
Notice last line is a matrix multiplication of
row vector 
by matrix 
.
A special : if we put 
and 
then
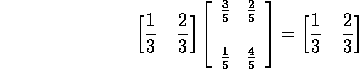
So: if 
then 
and analogously for W. This means that 
and 
have the
same distribution.
A probability vector is called the initial distribution for
the chain if
A Markov Chain is stationary if
for all i
Finding stationary initial distributions. Consider
above. The equation
is really
The first can be rearranged to
and so can the second. If is to be a
probability vector then
so we get
leading to
Some more examples:
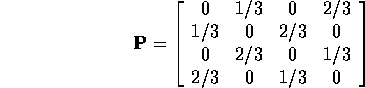
Set 
and get
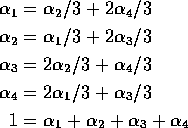
First plus third gives
so both sums 1/2. Continue algebra to get
p:=matrix([[0,1/3,0,2/3],[1/3,0,2/3,0],
[0,2/3,0,1/3],[2/3,0,1/3,0]]);
[ 0 1/3 0 2/3]
[ ]
[1/3 0 2/3 0 ]
p := [ ]
[ 0 2/3 0 1/3]
[ ]
[2/3 0 1/3 0 ]
> p2:=evalm(p*p);
[5/9 0 4/9 0 ]
[ ]
[ 0 5/9 0 4/9]
p2:= [ ]
[4/9 0 5/9 0 ]
[ ]
[ 0 4/9 0 5/9]
> p4:=evalm(p2*p2):
> p8:=evalm(p4*p4):
> p16:=evalm(p8*p8):
> p17:=evalm(p8*p8*p):
> evalf(evalm(p16));
[.5000000116 , 0 , .4999999884 , 0]
[ ]
[0 , .5000000116 , 0 , .4999999884]
[ ]
[.4999999884 , 0 , .5000000116 , 0]
[ ]
[0 , .4999999884 , 0 , .5000000116]
> evalf(evalm(p17));
[0 , .4999999961 , 0 , .5000000039]
[ ]
[.4999999961 , 0 , .5000000039 , 0]
[ ]
[0 , .5000000039 , 0 , .4999999961]
[ ]
[.5000000039 , 0 , .4999999961 , 0]
> evalf(evalm((p16+p17)/2));
[.2500, .2500, .2500, .2500]
[ ]
[.2500, .2500, .2500, .2500]
[ ]
[.2500, .2500, .2500, .2500]
[ ]
[.2500, .2500, .2500, .2500]
doesn't converges but 
does.
Next example:
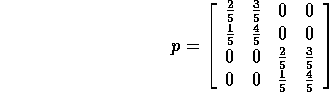
Solve :
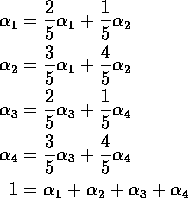
Second and fourth equations redundant. Get
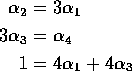
Pick 
in [0,1/4];
put 
.
solves .
So solution is not unique.
> p:=matrix([[2/5,3/5,0,0],[1/5,4/5,0,0],
[0,0,2/5,3/5],[0,0,1/5,4/5]]);
[2/5 3/5 0 0 ]
[ ]
[1/5 4/5 0 0 ]
p := [ ]
[ 0 0 2/5 3/5]
[ ]
[ 0 0 1/5 4/5]
> p2:=evalm(p*p):
> p4:=evalm(p2*p2):
> p8:=evalm(p4*p4):
> evalf(evalm(p8*p8));
[.2500000000 , .7500000000 , 0 , 0]
[ ]
[.2500000000 , .7500000000 , 0 , 0]
[ ]
[0 , 0 , .2500000000 , .7500000000]
[ ]
[0 , 0 , .2500000000 , .7500000000]
Notice that rows converge but to two different vectors:
and
Solutions of revisited?
Check that
and
If 
( 
) then
so again solution is not unique. Last example:
> p:=matrix([[2/5,3/5,0],[1/5,4/5,0],
[1/2,0,1/2]]);
[2/5 3/5 0 ]
[ ]
p := [1/5 4/5 0 ]
[ ]
[1/2 0 1/2]
> p2:=evalm(p*p):
> p4:=evalm(p2*p2):
> p8:=evalm(p4*p4):
> evalf(evalm(p8*p8));
[.2500000000 .7500000000 0 ]
[ ]
[.2500000000 .7500000000 0 ]
[ ]
[.2500152588 .7499694824 .00001525878906]
Interpretation of examples
all rows converge to some . In
this case this is a stationary initial distribution. the locations of zeros flip flop. does
not converge. Observation: average
does converge.
some rows converge to one and some to
another. In this case the solution of is not
unique.
Basic distinguishing features: pattern of 0s in matrix .
The ergodic theorem
Consider a finite state space chain.
If x is a vector then the ith entry in 
is
Rows of probability vectors, so a
weighted average of the entries in x.
If the weights are
strictly between 0 and 1 and the largest and smallest entries
in x are not the same then 
is strictly
between the largest and smallest entries in x. In fact
and
Now multiply 
by 
.
ijth entry in 
is a weighted average of the jth
column of .
So, if all the entries in row i of
are positive and the jth column of is not constant, the
ith entry in the jth column of must be strictly
between the minimum and maximum entries of the jth column of
.
In fact, fix a j.
maximum entry in column j of
the minimum
entry.
Suppose all entries of are positive.
Let 
be the smallest entry in . Our argument above
shows that
and
Putting these together gives
In summary the column maximum decreases, the column minimum increases
and the gap between the two decreases exponentially along
the sequence 
.
This idea can be used to prove
Proof: First for k>r
For each i there is a k for which 
and since
we see 
.
The argument before the proposition shows that
exists for each m and 
. This proves has a limit which
we call 
. Since 
also converges to we
find
Hence each row of is a solution of 
. The argument
before the statement of the proposition shows all rows of are equal.
Let 
be this common row.
Now if is any vector whose entries sum to 1
then 
converges to
If is any solution of 
we have by induction
so 
so 
.
That is exactly one vector whose entries sum to 1 satisfies .
Note conditions:
There is an r for which all entries in are positive.
The chain has a finite state space.
Consider finite state space case:
need not have limit. Example:
Note 
is the identity while 
.
Note, too, that
Consider the equations 
with 
.
We get
so that the solution to is again unique.
Definition: The period d of a state i is the greatest common divisor of
Definition: A state is aperiodic if its period is 1.
Proof: I do the case d=1. Fix i. Let
If 
then 
.
This (and aperiodic) implies (number theory argument) that there is an r such
that implies 
.
Now find m and n so that
For k>r+m+n we see 
so the gcd of the
set of k such that is 1.
The case of period d>1 can be dealt with by considering
.
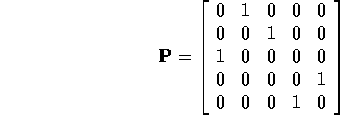
For this example 
is a class of period 3 states
and 
a class of period 2 states.
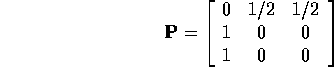
has a single communicating class of period 2.
A chain is aperiodic if all its states are aperiodic.