![]()
![]()
![]() Postscript version of this file
Postscript version of this file
Meaning of unconditional expected values?
Markov property specifies only conditional probabilities; no way to deduce marginal distributions.
For every distribution ![]() on S and transition matrix
on S and transition matrix ![]() there is a
a stochastic process
there is a
a stochastic process
![]() with
with
Notice Strong Markov Property proof used only conditional expectations.
Notation: ![]() a probability on S.
a probability on S.
![]() and
and ![]() are expected values and probabilities for chain with initial
distribution
are expected values and probabilities for chain with initial
distribution ![]() .
.
Summary of easily verified facts:
![]() For any sequence of states
For any sequence of states
![]()
![]() For any event A:
For any event A:
![]() For any bounded rv
For any bounded rv
![]()
Now consider a transient state k, that is, a state for which
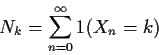
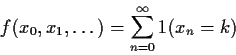
In short:
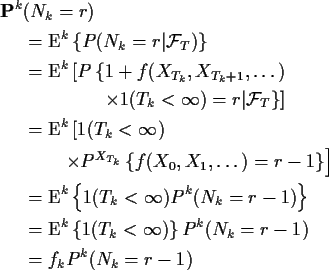
It is easily verified by induction, then, that
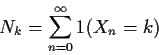
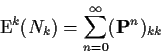
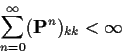
Proof: Suppose i is recurrent and
![]() .
There are integers
m and n such that
.
There are integers
m and n such that

A finite state space chain has at least one recurrent state:
If all states we transient we would have for each k
![]() .
This would mean
.
This would mean
![]() .
But for any
.
But for any ![]() there must be at least one k for which
there must be at least one k for which
![]() (the total of a finite list of finite numbers is finite).
(the total of a finite list of finite numbers is finite).
Infinite state space chain may have all states transient:
The chain Xn satisfying Xn+1=Xn+1 on the integers has all states transient.
More interesting example:
![]() Toss a coin repeatedly.
Toss a coin repeatedly.
![]() Let
Xn be X0 plus the number of heads minus the number of tails
in the first n tosses.
Let
Xn be X0 plus the number of heads minus the number of tails
in the first n tosses.
![]() Let p denote the probability of heads
on an individual trial.
Let p denote the probability of heads
on an individual trial.
Xn-X0 is a sum of n iid random variables Yiwhere P(Yi=1)=p and P(Yi=-1)=1-p.
SLLN shows Xn/n converges almost surely to 2p-1. If
![]() this is not 0.
this is not 0.
In order for Xn/n to have a
positive limit we must have
![]() almost surely so
all states are visited only finitely many times. That is, all
states are transient. Similarly for p<1/2
almost surely so
all states are visited only finitely many times. That is, all
states are transient. Similarly for p<1/2
![]() almost surely and all states are transient.
almost surely and all states are transient.
Now look at p=1/2. The law of large numbers argument no long shows anything. I will show that all states are recurrent.
Proof: We show
![]() and show the sum is infinite.
If n is odd then
(pn)00 = 0 so we evaluate
and show the sum is infinite.
If n is odd then
(pn)00 = 0 so we evaluate
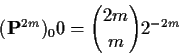
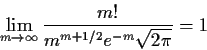
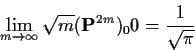
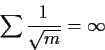
Compute expected times to return.
For ![]() let Tx denote the hitting time for
x.
let Tx denote the hitting time for
x.
Suppose x recurrent in irreducible chain (only one communicating class).
Derive equations for expected values of different Tx.
Each Tx is a certain function fx applied to
![]() .
Setting
.
Setting
![]() we find
we find
This gives
Here is a simple example:
![\begin{displaymath}{\bf P}= \left[\begin{array}{ccc}
0 & \frac{1}{2} & \frac{1}{...
...ac{1}{2}
\\
\frac{1}{2} & \frac{1}{2} & 0
\end{array}\right]
\end{displaymath}](img57.gif)
The identity (1) becomes
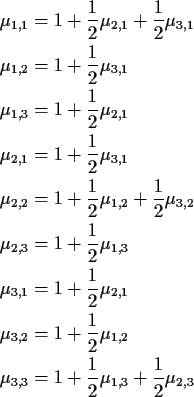
Seventh and fourth show
![]() .
Similar
calculations lead to
.
Similar
calculations lead to
![]() and, for
and, for ![]()
![]() .
.
Example: The coin tossing Markov Chain with p=1/2 shows
that the situation can be different when S is infinite.
The equations above become:
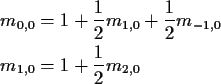
and many more.
Some observations:
You have to go through 1 to get to 0 from 2 so
Symmetry (switching H and T):
The transition probabilities are homogeneous:
Conclusion:
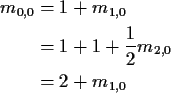
Notice that there are no finite solutions!
Summary of the situation:
Every state is recurrent.
All the expected hitting times mij are infinite.
All entries
![]() converge to 0.
converge to 0.
Jargon: The states in this chain are null recurrent.