Postscript version of this file

STAT 870 Lecture 13

Equivalence of Modelling Approaches

All 3 approaches to Poisson process are equivalent. I show: 3 implies 1, 1 implies 2 and 2 implies 3. First explain o, O.

Model 3 implies 1: Fix t, define to be conditional probability of 0 points in (t,t+s] given value of process on [0,t].

Derive differential equation for f. Given process on [0,t] and 0 points in (t,t+s] probability of no points in (t,t+s+h] is

Given the process on [0,t] the probability of no points in (t,t+s] is . Using P(AB|C)=P(A|BC)P(B|C) gives

Now rearrange, divide by h to get

Let and find

Differential equation has solution

Things to notice:

• is survival function of exponential rv..
• We had suppressed dependence of on but solution does not depend on condition.
• So: the event of getting 0 points in (t,t+s] is independent of .
• We used: . Other rules:

  

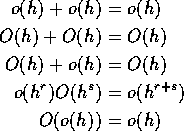
General case:

Notation: N(t) =N(0,t).

N(t) is a non-decreasing function of t. Let

Evaluate by conditioning on and N(t)=j.

Given N(t)=j probability that N(t+h) = k is conditional probability of k-j points in (t,t+h].

So, for :

For j=k-1 we have

For j=k we have

N is increasing so only consider .

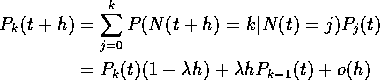
Rearrange, divide by h and let t get

For k=0 the term is dropped and

Using we get

Put this into the equation for k=1 to get

Multiply by to see

With we get

For general k we have and

Check by induction that

Hence: N(t) has Poisson distribution.

Similar ideas permit proof of

From which (by induction) we can prove that N has independent Poisson increments.

Exponential Interarrival Times

If N is a Poisson Process we define to be the times between 0 and the first point, the first point and the second and so on.

Fact: are iid exponential rvs with mean .

We already did rigorously. The event T;SPMgt;t is exactly the event N(t)=0. So

which is the survival function of an exponential rv.

I do case of . Let be two positive numbers and , . The event

This is almost the same as the intersection of the four events:

which has probability

Divide by and let and go to 0 to get joint density of is

which is the joint density of two independent exponential variates.

More rigor:

• Find joint density of .
• Use change of variables to find joint density of .

First step: Compute

This is just the event of exactly 1 point in each interval for ( ) and at least one point in which has probability

Second step: write this in terms of joint cdf of . I do k=2:

Notice tacit assumption .

Differentiate twice, that is, take

to get

Simplify to

Recall tacit assumption to get

That completes the first part.

Now compute the joint cdf of by

This is

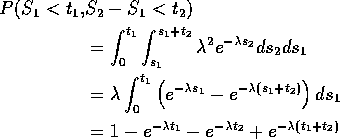
Differentiate twice to get

which is the joint density of two independent exponential random variables.

Summary so far:

Have shown:

Instantaneous rates model implies independent Poisson increments model implies independent exponential interarrivals.

Next: show independent exponential interarrivals implies the instantaneous rates model.

Suppose iid exponential rvs with means . Define by if and only if

Let A be the event . We are to show

and

If n(s) is a possible trajectory consistent with N(t) = k then n has jumps at points

and at no other points in (0,t].

So given with n(t)=k we are essentially being given

and asked the conditional probabilty in the first case of the event B given by

Conditioning on irrelevant (independence).

The numerator may be evaluated by integration:

Let to get the limit

as required.

The computation of

is similar.

Properties of exponential rvs

Convolution: If X and Y independent rvs with densities f and g respectively and Z=X+Y then

Differentiating wrt z we get

This integral is called the convolution of densities f and g.

If iid Exponential then has a Gamma distribution. Density of is

for s;SPMgt;0.

Proof:

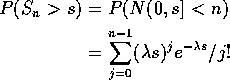
Then

This telescopes to

Extreme Values: If are independent exponential rvs with means then has an exponential distribution with mean

Proof:

Memoryless Property: conditional distribution of X-x given is exponential if X has an exponential distribution.

Proof:

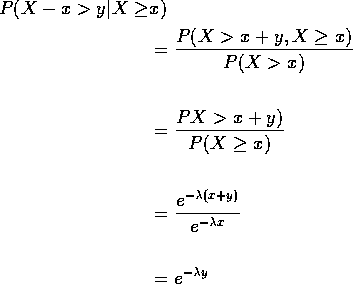
Hazard Rates

The hazard rate, or instantaneous failure rate for a positive random variable T with density f and cdf F is

This is just

For an exponential random variable with mean this is

The exponential distribution has constant failure rate.

Weibull random variables have density

for t;SPMgt;0. The corresponding survival function is

and the hazard rate is

which is increasing for , decreasing for . For this is the exponential distribution.

Since

we can integrate to find

so that r determines F and f.