

Any distribution supported on 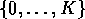 with a mean differing
by say
with a mean differing
by say
 from the nearest integer must belong to the set
from the nearest integer must belong to the set
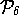 of the previous section for
of the previous section for 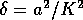 . Thus
for large enough
. Thus
for large enough  the set
the set  is a subset of
is a subset of 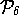 for some positive
for some positive 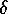 .
According to Theorem 1
.
According to Theorem 1
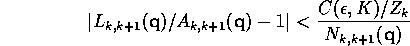
for all  in
in 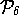 .
In view of the inequality
.
In view of the inequality
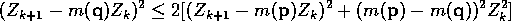
and 7 above we find
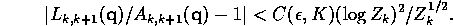
On the explosion set there is a 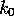 (random) such that the right
hand of this
inequality is less than
(random) such that the right
hand of this
inequality is less than  for all
for all  . A Taylor
expansion of the
logarithm thus shows
. A Taylor
expansion of the
logarithm thus shows
for all large 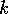 and all
and all  in
in 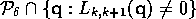 .
Since
.
Since
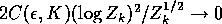 almost surely the lemma is
proved.
almost surely the lemma is
proved.