Example 27.1: Fisher's Iris Data
The iris data published by Fisher (1936) have been widely used
for examples in discriminant analysis and cluster analysis.
The sepal length, sepal width, petal length, and petal width
are measured in millimeters on fifty iris specimens from
each of three species, Iris setosa, I. versicolor,
and I. virginica. Mezzich and Solomon (1980) discuss
a variety of cluster analyses of the iris data.
In this example, the FASTCLUS procedure is
used to find two and, then, three clusters.
An output data set is created, and PROC FREQ is invoked
to compare the clusters with the species classification.
See Output 27.1.1 and
Output 27.1.2 for these results.
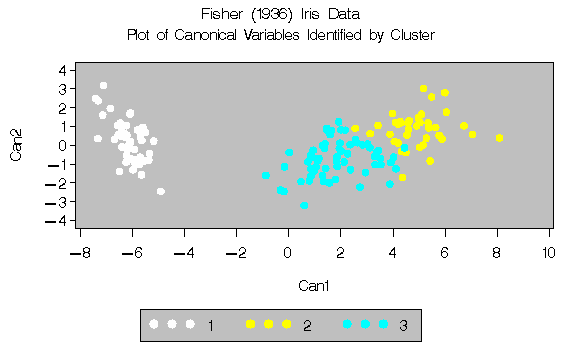
For three clusters, you can use the CANDISC procedure to
compute canonical variables for plotting the clusters.
See Output 27.1.3 for the results.
proc format;
value specname
1='Setosa '
2='Versicolor'
3='Virginica ';
run;
data iris;
title 'Fisher (1936) Iris Data';
input SepalLength SepalWidth PetalLength PetalWidth Species @@;
format Species specname.;
label SepalLength='Sepal Length in mm.'
SepalWidth ='Sepal Width in mm.'
PetalLength='Petal Length in mm.'
PetalWidth ='Petal Width in mm.';
symbol = put(species, specname10.);
datalines;
50 33 14 02 1 64 28 56 22 3 65 28 46 15 2 67 31 56 24 3
63 28 51 15 3 46 34 14 03 1 69 31 51 23 3 62 22 45 15 2
59 32 48 18 2 46 36 10 02 1 61 30 46 14 2 60 27 51 16 2
65 30 52 20 3 56 25 39 11 2 65 30 55 18 3 58 27 51 19 3
68 32 59 23 3 51 33 17 05 1 57 28 45 13 2 62 34 54 23 3
77 38 67 22 3 63 33 47 16 2 67 33 57 25 3 76 30 66 21 3
49 25 45 17 3 55 35 13 02 1 67 30 52 23 3 70 32 47 14 2
64 32 45 15 2 61 28 40 13 2 48 31 16 02 1 59 30 51 18 3
55 24 38 11 2 63 25 50 19 3 64 32 53 23 3 52 34 14 02 1
49 36 14 01 1 54 30 45 15 2 79 38 64 20 3 44 32 13 02 1
67 33 57 21 3 50 35 16 06 1 58 26 40 12 2 44 30 13 02 1
77 28 67 20 3 63 27 49 18 3 47 32 16 02 1 55 26 44 12 2
50 23 33 10 2 72 32 60 18 3 48 30 14 03 1 51 38 16 02 1
61 30 49 18 3 48 34 19 02 1 50 30 16 02 1 50 32 12 02 1
61 26 56 14 3 64 28 56 21 3 43 30 11 01 1 58 40 12 02 1
51 38 19 04 1 67 31 44 14 2 62 28 48 18 3 49 30 14 02 1
51 35 14 02 1 56 30 45 15 2 58 27 41 10 2 50 34 16 04 1
46 32 14 02 1 60 29 45 15 2 57 26 35 10 2 57 44 15 04 1
50 36 14 02 1 77 30 61 23 3 63 34 56 24 3 58 27 51 19 3
57 29 42 13 2 72 30 58 16 3 54 34 15 04 1 52 41 15 01 1
71 30 59 21 3 64 31 55 18 3 60 30 48 18 3 63 29 56 18 3
49 24 33 10 2 56 27 42 13 2 57 30 42 12 2 55 42 14 02 1
49 31 15 02 1 77 26 69 23 3 60 22 50 15 3 54 39 17 04 1
66 29 46 13 2 52 27 39 14 2 60 34 45 16 2 50 34 15 02 1
44 29 14 02 1 50 20 35 10 2 55 24 37 10 2 58 27 39 12 2
47 32 13 02 1 46 31 15 02 1 69 32 57 23 3 62 29 43 13 2
74 28 61 19 3 59 30 42 15 2 51 34 15 02 1 50 35 13 03 1
56 28 49 20 3 60 22 40 10 2 73 29 63 18 3 67 25 58 18 3
49 31 15 01 1 67 31 47 15 2 63 23 44 13 2 54 37 15 02 1
56 30 41 13 2 63 25 49 15 2 61 28 47 12 2 64 29 43 13 2
51 25 30 11 2 57 28 41 13 2 65 30 58 22 3 69 31 54 21 3
54 39 13 04 1 51 35 14 03 1 72 36 61 25 3 65 32 51 20 3
61 29 47 14 2 56 29 36 13 2 69 31 49 15 2 64 27 53 19 3
68 30 55 21 3 55 25 40 13 2 48 34 16 02 1 48 30 14 01 1
45 23 13 03 1 57 25 50 20 3 57 38 17 03 1 51 38 15 03 1
55 23 40 13 2 66 30 44 14 2 68 28 48 14 2 54 34 17 02 1
51 37 15 04 1 52 35 15 02 1 58 28 51 24 3 67 30 50 17 2
63 33 60 25 3 53 37 15 02 1
;
proc fastclus data=iris maxc=2 maxiter=10 out=clus;
var SepalLength SepalWidth PetalLength PetalWidth;
run;
proc freq;
tables cluster*species;
run;
proc fastclus data=iris maxc=3 maxiter=10 out=clus;
var SepalLength SepalWidth PetalLength PetalWidth;
run;
proc freq;
tables cluster*Species;
run;
proc candisc anova out=can;
class cluster;
var SepalLength SepalWidth PetalLength PetalWidth;
title2 'Canonical Discriminant Analysis of Iris Clusters';
run;
legend1 frame cframe=ligr label=none cborder=black
position=center value=(justify=center);
axis1 label=(angle=90 rotate=0) minor=none;
axis2 minor=none;
proc gplot data=Can;
plot Can2*Can1=Cluster/frame cframe=ligr
legend=legend1 vaxis=axis1 haxis=axis2;
title2 'Plot of Canonical Variables Identified by Cluster';
run;
Output 27.1.1: Fisher's Iris Data: PROC FASTCLUS
with MAXC=2 and PROC FREQ
|
| The FASTCLUS Procedure |
| Replace=FULL Radius=0 Maxclusters=2 Maxiter=10 Converge=0.02 |
| Initial Seeds |
| Cluster |
SepalLength |
SepalWidth |
PetalLength |
PetalWidth |
| 1 |
43.00000000 |
30.00000000 |
11.00000000 |
1.00000000 |
| 2 |
77.00000000 |
26.00000000 |
69.00000000 |
23.00000000 |
| Minimum Distance Between Initial Seeds = |
70.85196 |
|
|
| The FASTCLUS Procedure |
| Replace=FULL Radius=0 Maxclusters=2 Maxiter=10 Converge=0.02 |
| Iteration History |
| Iteration |
Criterion |
Relative Change in Cluster
Seeds |
| 1 |
2 |
| 1 |
11.0638 |
0.1904 |
0.3163 |
| 2 |
5.3780 |
0.0596 |
0.0264 |
| 3 |
5.0718 |
0.0174 |
0.00766 |
| Convergence criterion is satisfied. |
| Criterion Based on Final Seeds = |
5.0417 |
| Cluster Summary |
| Cluster |
Frequency |
RMS Std Deviation |
Maximum Distance
from Seed
to Observation |
Radius
Exceeded |
Nearest Cluster |
Distance Between
Cluster Centroids |
| 1 |
53 |
3.7050 |
21.1621 |
|
2 |
39.2879 |
| 2 |
97 |
5.6779 |
24.6430 |
|
1 |
39.2879 |
| Statistics for Variables |
| Variable |
Total STD |
Within STD |
R-Square |
RSQ/(1-RSQ) |
| SepalLength |
8.28066 |
5.49313 |
0.562896 |
1.287784 |
| SepalWidth |
4.35866 |
3.70393 |
0.282710 |
0.394137 |
| PetalLength |
17.65298 |
6.80331 |
0.852470 |
5.778291 |
| PetalWidth |
7.62238 |
3.57200 |
0.781868 |
3.584390 |
| OVER-ALL |
10.69224 |
5.07291 |
0.776410 |
3.472463 |
| Pseudo F Statistic = |
513.92 |
| Approximate Expected Over-All R-Squared = |
0.51539 |
| Cubic Clustering Criterion = |
14.806 |
| WARNING: The two above values are invalid for correlated variables. |
|
|
| The FASTCLUS Procedure |
| Replace=FULL Radius=0 Maxclusters=2 Maxiter=10 Converge=0.02 |
| Cluster Means |
| Cluster |
SepalLength |
SepalWidth |
PetalLength |
PetalWidth |
| 1 |
50.05660377 |
33.69811321 |
15.60377358 |
2.90566038 |
| 2 |
63.01030928 |
28.86597938 |
49.58762887 |
16.95876289 |
| Cluster Standard Deviations |
| Cluster |
SepalLength |
SepalWidth |
PetalLength |
PetalWidth |
| 1 |
3.427350930 |
4.396611045 |
4.404279486 |
2.105525249 |
| 2 |
6.336887455 |
3.267991438 |
7.800577673 |
4.155612484 |
|
|
Frequency
Percent
Row Pct
Col Pct |
|
| Table of CLUSTER by Species |
| CLUSTER(Cluster |
Species |
Total |
| Setosa |
Versicolor |
Virginica |
| 1 |
50
33.33
94.34
100.00 |
3
2.00
5.66
6.00 |
0
0.00
0.00
0.00 |
53
35.33
|
| 2 |
0
0.00
0.00
0.00 |
47
31.33
48.45
94.00 |
50
33.33
51.55
100.00 |
97
64.67
|
| Total |
50
33.33 |
50
33.33 |
50
33.33 |
150
100.00 |
|
|
Output 27.1.2: Fisher's Iris Data: PROC FASTCLUS
with MAXC=3 and PROC FREQ
|
| The FASTCLUS Procedure |
| Replace=FULL Radius=0 Maxclusters=3 Maxiter=10 Converge=0.02 |
| Initial Seeds |
| Cluster |
SepalLength |
SepalWidth |
PetalLength |
PetalWidth |
| 1 |
58.00000000 |
40.00000000 |
12.00000000 |
2.00000000 |
| 2 |
77.00000000 |
38.00000000 |
67.00000000 |
22.00000000 |
| 3 |
49.00000000 |
25.00000000 |
45.00000000 |
17.00000000 |
| Minimum Distance Between Initial Seeds = |
38.23611 |
|
|
| The FASTCLUS Procedure |
| Replace=FULL Radius=0 Maxclusters=3 Maxiter=10 Converge=0.02 |
| Iteration History |
| Iteration |
Criterion |
Relative Change in Cluster Seeds |
| 1 |
2 |
3 |
| 1 |
6.7591 |
0.2652 |
0.3205 |
0.2985 |
| 2 |
3.7097 |
0 |
0.0459 |
0.0317 |
| 3 |
3.6427 |
0 |
0.0182 |
0.0124 |
| Convergence criterion is satisfied. |
| Criterion Based on Final Seeds = |
3.6289 |
| Cluster Summary |
| Cluster |
Frequency |
RMS Std Deviation |
Maximum Distance
from Seed
to Observation |
Radius
Exceeded |
Nearest Cluster |
Distance Between
Cluster Centroids |
| 1 |
50 |
2.7803 |
12.4803 |
|
3 |
33.5693 |
| 2 |
38 |
4.0168 |
14.9736 |
|
3 |
17.9718 |
| 3 |
62 |
4.0398 |
16.9272 |
|
2 |
17.9718 |
| Statistics for Variables |
| Variable |
Total STD |
Within STD |
R-Square |
RSQ/(1-RSQ) |
| SepalLength |
8.28066 |
4.39488 |
0.722096 |
2.598359 |
| SepalWidth |
4.35866 |
3.24816 |
0.452102 |
0.825156 |
| PetalLength |
17.65298 |
4.21431 |
0.943773 |
16.784895 |
| PetalWidth |
7.62238 |
2.45244 |
0.897872 |
8.791618 |
| OVER-ALL |
10.69224 |
3.66198 |
0.884275 |
7.641194 |
| Pseudo F Statistic = |
561.63 |
| Approximate Expected Over-All R-Squared = |
0.62728 |
| Cubic Clustering Criterion = |
25.021 |
| WARNING: The two above values are invalid for correlated variables. |
|
|
| The FASTCLUS Procedure |
| Replace=FULL Radius=0 Maxclusters=3 Maxiter=10 Converge=0.02 |
| Cluster Means |
| Cluster |
SepalLength |
SepalWidth |
PetalLength |
PetalWidth |
| 1 |
50.06000000 |
34.28000000 |
14.62000000 |
2.46000000 |
| 2 |
68.50000000 |
30.73684211 |
57.42105263 |
20.71052632 |
| 3 |
59.01612903 |
27.48387097 |
43.93548387 |
14.33870968 |
| Cluster Standard Deviations |
| Cluster |
SepalLength |
SepalWidth |
PetalLength |
PetalWidth |
| 1 |
3.524896872 |
3.790643691 |
1.736639965 |
1.053855894 |
| 2 |
4.941550255 |
2.900924461 |
4.885895746 |
2.798724562 |
| 3 |
4.664100551 |
2.962840548 |
5.088949673 |
2.974997167 |
|
|
Frequency
Percent
Row Pct
Col Pct |
|
| Table of CLUSTER by Species |
| CLUSTER(Cluster |
Species |
Total |
| Setosa |
Versicolor |
Virginica |
| 1 |
50
33.33
100.00
100.00 |
0
0.00
0.00
0.00 |
0
0.00
0.00
0.00 |
50
33.33
|
| 2 |
0
0.00
0.00
0.00 |
2
1.33
5.26
4.00 |
36
24.00
94.74
72.00 |
38
25.33
|
| 3 |
0
0.00
0.00
0.00 |
48
32.00
77.42
96.00 |
14
9.33
22.58
28.00 |
62
41.33
|
| Total |
50
33.33 |
50
33.33 |
50
33.33 |
150
100.00 |
|
|
Output 27.1.3: Fisher's Iris Data: PROC CANDISC and PROC GPLOT
|
| Fisher (1936) Iris Data |
| Canonical Discriminant Analysis of Iris Clusters |
| Observations |
150 |
DF Total |
149 |
| Variables |
4 |
DF Within Classes |
147 |
| Classes |
3 |
DF Between Classes |
2 |
| Class Level Information |
| CLUSTER |
Variable
Name |
Frequency |
Weight |
Proportion |
| 1 |
_1 |
50 |
50.0000 |
0.333333 |
| 2 |
_2 |
38 |
38.0000 |
0.253333 |
| 3 |
_3 |
62 |
62.0000 |
0.413333 |
|
|
| Fisher (1936) Iris Data |
| Canonical Discriminant Analysis of Iris Clusters |
| Univariate Test Statistics |
| F Statistics, Num DF=2, Den DF=147 |
| Variable |
Label |
Total
Standard
Deviation |
Pooled
Standard
Deviation |
Between
Standard
Deviation |
R-Square |
R-Square
/ (1-RSq) |
F Value |
Pr > F |
| SepalLength |
Sepal Length in mm. |
8.2807 |
4.3949 |
8.5893 |
0.7221 |
2.5984 |
190.98 |
<.0001 |
| SepalWidth |
Sepal Width in mm. |
4.3587 |
3.2482 |
3.5774 |
0.4521 |
0.8252 |
60.65 |
<.0001 |
| PetalLength |
Petal Length in mm. |
17.6530 |
4.2143 |
20.9336 |
0.9438 |
16.7849 |
1233.69 |
<.0001 |
| PetalWidth |
Petal Width in mm. |
7.6224 |
2.4524 |
8.8164 |
0.8979 |
8.7916 |
646.18 |
<.0001 |
| Average R-Square |
| Unweighted |
0.7539604 |
| Weighted by Variance |
0.8842753 |
| Multivariate Statistics and F Approximations |
| S=2 M=0.5 N=71 |
| Statistic |
Value |
F Value |
Num DF |
Den DF |
Pr > F |
| Wilks' Lambda |
0.03222337 |
164.55 |
8 |
288 |
<.0001 |
| Pillai's Trace |
1.25669612 |
61.29 |
8 |
290 |
<.0001 |
| Hotelling-Lawley Trace |
21.06722883 |
377.66 |
8 |
203.4 |
<.0001 |
| Roy's Greatest Root |
20.63266809 |
747.93 |
4 |
145 |
<.0001 |
| NOTE: |
F Statistic for Roy's Greatest Root is an upper bound. |
|
| NOTE: |
F Statistic for Wilks' Lambda is exact. |
|
|
|
| Fisher (1936) Iris Data |
| Canonical Discriminant Analysis of Iris Clusters |
| |
Canonical
Correlation |
Adjusted
Canonical
Correlation |
Approximate
Standard
Error |
Squared
Canonical
Correlation |
Eigenvalues of Inv(E)*H
= CanRsq/(1-CanRsq) |
Test of H0: The canonical correlations in the current row and all that follow are zero |
| |
Eigenvalue |
Difference |
Proportion |
Cumulative |
Likelihood
Ratio |
Approximate
F Value |
Num DF |
Den DF |
Pr > F |
| 1 |
0.976613 |
0.976123 |
0.003787 |
0.953774 |
20.6327 |
20.1981 |
0.9794 |
0.9794 |
0.03222337 |
164.55 |
8 |
288 |
<.0001 |
| 2 |
0.550384 |
0.543354 |
0.057107 |
0.302923 |
0.4346 |
|
0.0206 |
1.0000 |
0.69707749 |
21.00 |
3 |
145 |
<.0001 |
|
|
| Fisher (1936) Iris Data |
| Canonical Discriminant Analysis of Iris Clusters |
| Total Canonical Structure |
| Variable |
Label |
Can1 |
Can2 |
| SepalLength |
Sepal Length in mm. |
0.831965 |
0.452137 |
| SepalWidth |
Sepal Width in mm. |
-0.515082 |
0.810630 |
| PetalLength |
Petal Length in mm. |
0.993520 |
0.087514 |
| PetalWidth |
Petal Width in mm. |
0.966325 |
0.154745 |
| Between Canonical Structure |
| Variable |
Label |
Can1 |
Can2 |
| SepalLength |
Sepal Length in mm. |
0.956160 |
0.292846 |
| SepalWidth |
Sepal Width in mm. |
-0.748136 |
0.663545 |
| PetalLength |
Petal Length in mm. |
0.998770 |
0.049580 |
| PetalWidth |
Petal Width in mm. |
0.995952 |
0.089883 |
| Pooled Within Canonical Structure |
| Variable |
Label |
Can1 |
Can2 |
| SepalLength |
Sepal Length in mm. |
0.339314 |
0.716082 |
| SepalWidth |
Sepal Width in mm. |
-0.149614 |
0.914351 |
| PetalLength |
Petal Length in mm. |
0.900839 |
0.308136 |
| PetalWidth |
Petal Width in mm. |
0.650123 |
0.404282 |
|
|
| Fisher (1936) Iris Data |
| Canonical Discriminant Analysis of Iris Clusters |
| Total-Sample Standardized Canonical Coefficients |
| Variable |
Label |
Can1 |
Can2 |
| SepalLength |
Sepal Length in mm. |
0.047747341 |
1.021487262 |
| SepalWidth |
Sepal Width in mm. |
-0.577569244 |
0.864455153 |
| PetalLength |
Petal Length in mm. |
3.341309573 |
-1.283043758 |
| PetalWidth |
Petal Width in mm. |
0.996451144 |
0.900476563 |
| Pooled Within-Class Standardized Canonical Coefficients |
| Variable |
Label |
Can1 |
Can2 |
| SepalLength |
Sepal Length in mm. |
0.0253414487 |
0.5421446856 |
| SepalWidth |
Sepal Width in mm. |
-.4304161258 |
0.6442092294 |
| PetalLength |
Petal Length in mm. |
0.7976741592 |
-.3063023132 |
| PetalWidth |
Petal Width in mm. |
0.3205998034 |
0.2897207865 |
| Raw Canonical Coefficients |
| Variable |
Label |
Can1 |
Can2 |
| SepalLength |
Sepal Length in mm. |
0.0057661265 |
0.1233581748 |
| SepalWidth |
Sepal Width in mm. |
-.1325106494 |
0.1983303556 |
| PetalLength |
Petal Length in mm. |
0.1892773419 |
-.0726814163 |
| PetalWidth |
Petal Width in mm. |
0.1307270927 |
0.1181359305 |
| Class Means on Canonical Variables |
| CLUSTER |
Can1 |
Can2 |
| 1 |
-6.131527227 |
0.244761516 |
| 2 |
4.931414018 |
0.861972277 |
| 3 |
1.922300462 |
-0.725693908 |
|
Copyright © 1999 by SAS Institute Inc., Cary, NC, USA. All rights reserved.