Measures of Association

The FREQ Procedure

Measures of Association

When you specify the MEASURES option in the TABLES statement, PROC FREQ computes several statistics that describe the association between the two variables of the contingency table. The following are measures of ordinal association that consider whether the variable Y tends to increase as X increases: gamma, Kendall's tau-b, Stuart's tau-c, and Somers' D. These measures are appropriate for ordinal variables, and they classify pairs of observations as concordant or discordant. A pair is concordant if the observation with the larger value of X also has the larger value of Y. A pair is discordant if the observation with the larger value of X has the smaller value of Y. Refer to Agresti (1996) and the other references cited in the discussion of each measure of association.

The Pearson correlation coefficient and the Spearman rank correlation coefficient are also appropriate for ordinal variables. The Pearson correlation describes the strength of the linear association between the row and column variables, and it is computed using the row and column scores specified by the SCORES= option in the TABLES statement. The Spearman correlation is computed with rank scores. The polychoric correlation (requested by the PLCORR option) also requires ordinal variables and assumes that the variables have an underlying bivariate normal distribution. The following measures of association do not require ordinal variables, but they are appropriate for nominal variables: lambda asymmetric, lambda symmetric, and uncertainty coefficients.

PROC FREQ computes estimates of the measures according to the formulas given in the discussion of each measure of association. For each measure, PROC FREQ computes an asymptotic standard error (ASE), which is the square root of the asymptotic variance denoted by var in the following sections.

Confidence Limits

If you specify the CL option in the TABLES statement, PROC FREQ computes asymptotic confidence limits for all MEASURES statistics. The confidence coefficient is determined according to the value of the ALPHA= option, which by default equals 0.05 and produces 95% confidence limits.

The confidence limits are computed as

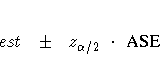
$est +- z_{\alpha/2} \cdot {ASE}$

where est is the estimate of the measure, $z_{\alpha/2}$ is the $100(1 - \alpha/2)$ percentile of the standard normal distribution, and ASE is the asymptotic standard error of the estimate.

Asymptotic Tests

For each measure that you specify in the TEST statement, PROC FREQ computes an asymptotic test of the null hypothesis that the measure equals zero. Asymptotic tests are available for the following measures of association: gamma, Kendall's tau-b, Stuart's tau-c, Somers' D(R|C), Somers' D(C|R), the Pearson correlation coefficient, and the Spearman rank correlation coefficient. To compute an asymptotic test, PROC FREQ uses a standardized test statistic z, which has an asymptotic standard normal distribution under the null hypothesis. The standardized test statistic is computed as

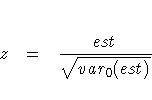
$z = \frac{est}{\sqrt{var_0(est)}}$

where est is the estimate of the measure and var₀(est) is the variance of the estimate under the null hypothesis. Formulas for var₀(est) are given in the discussion of each measure of association.

Note that the ratio of est to $\sqrt{var_0(est)}$ is the same for the following measures: gamma, Kendall's tau-b, Stuart's tau-c, Somers' D(R|C), and Somers' D(C|R). Therefore, the tests for these measures are identical. For example, the p-values for the test of H₀: gamma = 0 equal the p-values for the test of H₀: tau-b = 0.

PROC FREQ computes one-sided and two-sided p-values for each of these tests. When the test statistic z is greater than its null hypothesis expected value of zero, PROC FREQ computes the right-sided p-value, which is the probability of a larger value of the statistic occurring under the null hypothesis. A small right-sided p-value supports the alternative hypothesis that the true value of the measure is greater than zero. When the test statistic is less than or equal to zero, PROC FREQ computes the left-sided p-value, which is the probability of a smaller value of the statistic occurring under the null hypothesis. A small left-sided p-value supports the alternative hypothesis that the true value of the measure is less than zero. The one-sided p-value P₁ can be expressed as

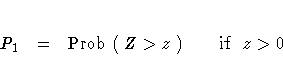
$P_{1} = {\rm Prob} (Z \gt z) {\rm if} z \gt 0$

$P_{1} = {\rm Prob} (Z \lt z) {\rm if} z \leq 0$

where Z has a standard normal distribution. The two-sided p-value P₂ is computed as

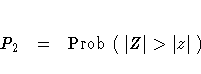
$P_{2} = {\rm Prob} (| Z| \gt | z|)$

Exact Tests

Exact tests are available for two measures of association, the Pearson correlation coefficient and the Spearman rank correlation coefficient. If you specify the PCORR option in the EXACT statement, PROC FREQ computes the exact test of the hypothesis that the Pearson correlation equals zero. If you specify the SCORR option in the EXACT statement, PROC FREQ computes the exact test of the hypothesis that the Spearman correlation equals zero. See the section "Exact Statistics" for information on exact tests.

Gamma

The estimator of gamma is based only on the number of concordant and discordant pairs of observations. It ignores tied pairs (that is, pairs of observations that have equal values of X or equal values of Y). Gamma is appropriate only when both variables lie on an ordinal scale. It has the range $-1 \leq \Gamma \leq 1$ . If the two variables are independent, then the estimator of gamma tends to be close to zero. Gamma is estimated by

G = [(P-Q)/(P + Q)]

with asymptotic variance

$var = \frac{16}{(P + Q)^4} \sum_i \sum_j n_{ij} (QA_{ij} - PD_{ij})^2$

The variance of the estimator under the null hypothesis that gamma equals zero is computed as

$var_0(G) = \frac{4}{(P+Q)^2} ( \sum_i \sum_j n_{ij} (A_{ij}-D_{ij})^2 - (P-Q)^2/n )$

For 2 ×2 tables, gamma is equivalent to Yule's Q. Refer to Goodman and Kruskal (1979), Agresti (1990), and Brown and Benedetti (1977).

Kendall's Tau-b

Kendall's tau-b is similar to gamma except that tau-b uses a correction for ties. Tau-b is appropriate only when both variables lie on an ordinal scale. Tau-b has the range $-1 \leq \tau_b \leq 1$ .It is estimated by

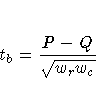
$t_b = \frac{P - Q}{\sqrt{w_r w_c}}$

with

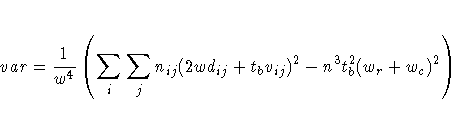
$var = \frac{1}{w^4} ( \sum_i \sum_j n_{ij} (2wd_{ij} + t_b v_{ij})^2 - n^3 t_b^2 (w_r + w_c)^2 )$

where

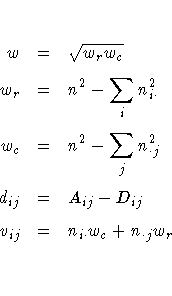
$w & = & \sqrt{w_r w_c} \ w_r & = & n^2 - \sum_i n_{i \cdot}^2 \ w_c & = & n^2 ... ...d_{ij} & = & A_{ij} - D_{ij} \ v_{ij} & = & n_{i \cdot} w_c + n_{\cdot j} w_r \$

The variance of the estimator under the null hypothesis that tau-b equals zero is computed as

$var_0(t_b) = \frac{4}{w_r w_c} ( \sum_i \sum_j n_{ij} (A_{ij} - D_{ij})^2 - (P-Q)^2/n )$

Refer to Kendall (1955) and Brown and Benedetti (1977).

Stuart's Tau-c

Stuart's tau-c makes an adjustment for table size in addition to a correction for ties. Tau-c is appropriate only when both variables lie on an ordinal scale. Tau-c has the range $-1 \leq \tau_c \leq 1$ .It is estimated by

t_c = [(m(P - Q))/(n²(m - 1))]

with

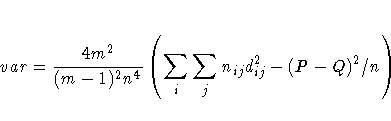
$var = \frac{4m^2}{(m - 1)^2 n^4} ( \sum_i \sum_j n_{ij} d_{ij}^2 - (P-Q)^2/n )$

where

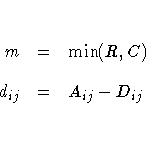
$m & = & \min (R,C) \ d_{ij} & = & A_{ij} - D_{ij} \$

The variance of the estimator under the null hypothesis that tau-c equals zero is

var₀(t_c) = var

Refer to Brown and Benedetti (1977).

Somers' D (C |R ) and D (R |C )

Somers' D(C|R) and Somers' D(R|C) are asymmetric modifications of tau-b. C|R denotes that the row variable X is regarded as an independent variable, while the column variable Y is regarded as dependent. Similarly, R|C denotes that the column variable Y is regarded as an independent variable, while the row variable X is regarded as dependent. Somers' D differs from tau-b in that it uses a correction only for pairs that are tied on the independent variable. Somers' D is appropriate only when both variables lie on an ordinal scale. It has the range $-1 \leq D \leq 1$ . Formulas for Somers' D(R|C) are obtained by interchanging the indices.

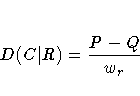
$D(C| R) = \frac{P - Q}{w_r}$

with

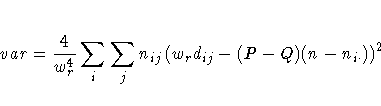
$var = \frac{4}{w_r^4} \sum_i \sum_j n_{ij} ( w_r d_{ij} - (P - Q)(n - n_{i \cdot}) )^2$

where

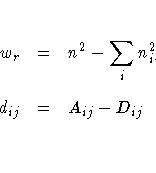
$w_r & = & n^2 - \sum_i n_{i \cdot}^2 \ d_{ij} & = & A_{ij} - D_{ij} \$

The variance of the estimator under the null hypothesis that D(C|R) equals zero is computed as

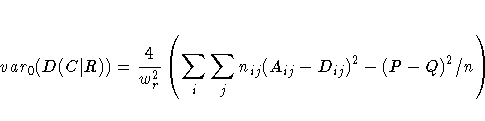
$var_0(D(C| R)) = \frac{4}{w_r^2} ( \sum_i \sum_j n_{ij} (A_{ij} - D_{ij})^2 - (P-Q)^2/n )$

Refer to Somers (1962), Goodman and Kruskal (1979), and Liebetrau (1983).

Pearson Correlation Coefficient

PROC FREQ computes the Pearson correlation coefficient using the scores specified in the SCORES= option. The Pearson correlation is appropriate only when both variables lie on an ordinal scale. It has the range $-1 \leq \rho \leq 1$ . The Pearson correlation coefficient is computed as

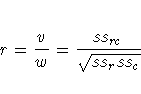
$r = \frac{v}w = \frac{ss_{rc}}{\sqrt{ss_r ss_c}}$

with

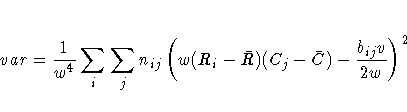
$var = \frac{1}{w^4} \sum_i \sum_j n_{ij} ( w (R_i - \bar{R}) (C_j - \bar{C}) - \frac{b_{ij} v}{2w} )^2$

The row scores R_i and the column scores C_j are determined by the SCORES= option in the TABLES statement, and

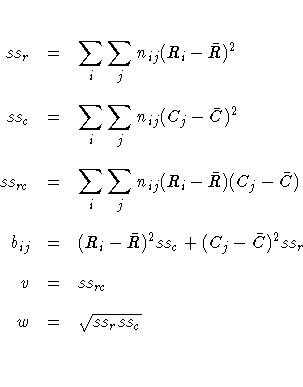
$ss_r & = & \sum_i \sum_j n_{ij} (R_i-\bar{R})^2 \ ss_c & = & \sum_i \sum_j n_{i... ...2 ss_c + (C_j-\bar{C})^2 ss_r \ v & = & ss_{rc} \ w & = & \sqrt{ss_r ss_c} \$

Refer to Snedecor and Cochran (1989) and Brown and Benedetti (1977).

To compute an asymptotic test for the Pearson correlation, PROC FREQ uses a standardized test statistic $r^{\ast}$ , which has an asymptotic standard normal distribution under the null hypothesis that the correlation equals zero. The standardized test statistic is computed as

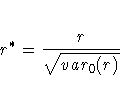
$r^{\ast} = \frac{r}{\sqrt{var_0(r)}}$

where var₀(r) is the variance of the correlation under the null hypothesis.

$var_0(r) = \frac{\sum_i \sum_j n_{ij} (R_i - \bar{R})^2 (C_j - \bar{C})^2 - ss_{rc}^2 / n} {ss_r ss_c}$

The asymptotic variance is derived for multinomial sampling in a contingency table framework, and it differs from the form obtained under the assumption that both variables are continuous and normally distributed. Refer to Brown and Benedetti (1977).

PROC FREQ also computes the exact test for the hypothesis that the Pearson correlation equals zero when you specify the PCORR option in the EXACT statement. See the section "Exact Statistics" for information on exact tests.

Spearman Rank Correlation Coefficient

The Spearman correlation coefficient is computed using rank scores R1_i and C1_j, defined in the section "Scores". It is appropriate only when both variables lie on an ordinal scale. It has the range $-1 \leq \rho_s \leq 1$ .The Spearman correlation coefficient is computed as

r_s = [v/w]

with

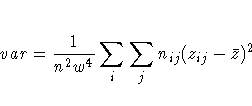
$var = \frac{1}{n^2 w^4} \sum_i \sum_j n_{ij} (z_{ij} - \bar{z})^2$

where

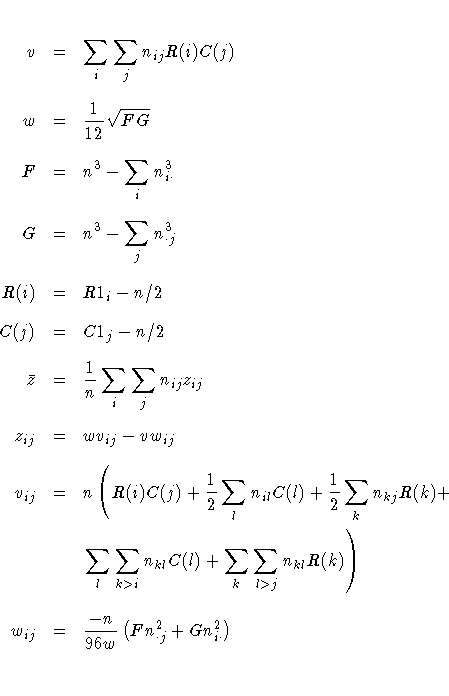
$v & = & \sum_i \sum_j n_{ij} R(i) C(j) \ w & = & \frac{1}{12} \sqrt{FG} \ F & ... ...k) ) \ w_{ij} & = & \frac{-n}{96w} ( F n_{\cdot j}^2 + G n_{i \cdot}^2 ) \$

Refer to Snedecor and Cochran (1989) and Brown and Benedetti (1977).

To compute an asymptotic test for the Spearman correlation, PROC FREQ uses a standardized test statistic $r_{s}^{\ast}$ ,which has an asymptotic standard normal distribution under the null hypothesis that the correlation equals zero. The standardized test statistic is computed as

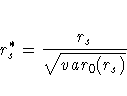
$r_{s}^{\ast} = \frac{r_s}{\sqrt{var_0(r_s)}}$

where var₀(r_s) is the variance of the correlation under the null hypothesis.

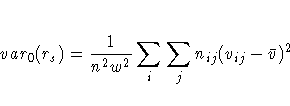
$var_0(r_s) = \frac{1}{n^2 w^2} \sum_i \sum_j n_{ij} (v_{ij} - \bar{v})^2$

where

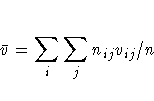
$\bar{v} = \sum_i \sum_j n_{ij} v_{ij} / n$

PROC FREQ also computes the exact test for the hypothesis that the Spearman rank correlation equals zero when you specify the SCORR option in the EXACT statement. See the section "Exact Statistics" for information on exact tests.

Polychoric Correlation

When you specify the PLCORR option in the TABLES statement, PROC FREQ computes the polychoric correlation. This measure of association is based on the assumption that the ordered, categorical variables of the frequency table have an underlying bivariate normal distribution. For 2 ×2 tables, the polychoric correlation is also known as the tetrachoric correlation. Refer to Drasgow (1986) for an overview of polychoric correlation. The polychoric correlation coefficient is the maximum likelihood estimate of the product-moment correlation between the normal variables, estimating thresholds from the observed table frequencies. The range of the polychoric correlation is from -1 to 1. Olsson (1979) gives the likelihood equations and an asymptotic covariance matrix for the estimates.

To estimate the polychoric correlation, PROC FREQ iteratively solves the likelihood equations by a Newton-Raphson algorithm using the Pearson correlation coefficient as the initial approximation. Iteration stops when the convergence measure falls below the convergence criterion or when the maximum number of iterations is reached, whichever occurs first. The CONVERGE= option sets the convergence criterion, and the default value is 0.0001. The MAXITER= option sets the maximum number of iterations, and the default value is 20.

Lambda Asymmetric

Asymmetric lambda, $\lambda(C| R)$ , is interpreted as the probable improvement in predicting the column variable Y given knowledge of the row variable X. Asymmetric lambda has the range $0 \leq \lambda(C| R) \leq 1$ . It is computed as

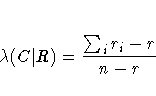
$\lambda (C| R) = \frac{\sum_i r_i - r}{n - r}$

with

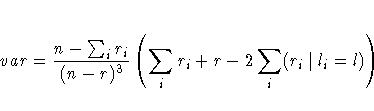
$var = \frac{n - \sum_i r_i}{(n - r)^3} ( \sum_i r_i + r - 2 \sum_i (r_i|l_i = l) )$

where

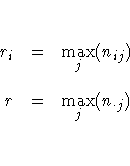
$r_i & = & \max_j (n_{ij}) \ r & = & \max_j (n_{\cdot j}) \$

Also, let l_i be the unique value of j such that r_i=n_ij, and let l be the unique value of j such that r = n_·j.

Because of the uniqueness assumptions, ties in the frequencies or in the marginal totals must be broken in an arbitrary but consistent manner. In case of ties, l is defined here as the smallest value of j such that r = n_·j. For a given i, if there is at least one value j such that n_ij=r_i=c_j, then l_i is defined here to be the smallest such value of j. Otherwise, if n_il=r_i, then l_i is defined to be equal to l. If neither condition is true, then l_i is taken to be the smallest value of j such that n_ij=r_i. The formulas for lambda asymmetric (R|C) can be obtained by interchanging the indices.

Refer to Goodman and Kruskal (1979).

Lambda Symmetric

The nondirectional lambda is the average of the two asymmetric lambdas, $\lambda(C| R)$ and $\lambda (R| C)$ .Lambda symmetric has the range $0 \leq \lambda \leq 1$ . Lambda symmetric is defined as

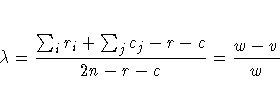
$\lambda = \frac{\sum_i r_i + \sum_j c_j - r - c}{2n - r - c} = \frac{w - v}w$

with

$var = \frac{1}{w^4} ( wvy - 2w^2 [ n-\sum_i \sum_j (n_{ij}|j=l_i,i=k_j) ] - 2v^2 (n - n_{kl}) )$

where

$c_j & = & \max_i (n_{ij}) \ c & = & \max_i (n_{i \cdot}) \ w & = & 2n - r - c... ... l_i=l ) + \sum_j (c_j | k_j=k) + r_k + c_l \ y & = & 8n - w - v - 2x \$

Refer to Goodman and Kruskal (1979).

Uncertainty Coefficients (C |R ) and (R |C )

The uncertainty coefficient, U(C|R), is the proportion of uncertainty (entropy) in the column variable Y that is explained by the row variable X. It has the range $0 \leq U(C| R) \leq 1$ . The formulas for U(R|C) can be obtained by interchanging the indices.

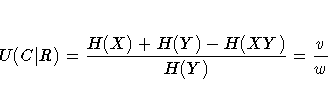
$U(C| R) = \frac{H(X) + H(Y) - H(XY)}{H(Y)} = \frac{v}w$

with

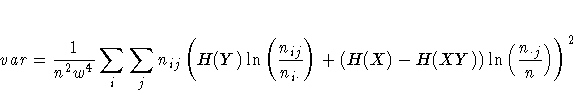
$var = \frac{1}{n^2 w^4} \sum_i \sum_j n_{ij} ( H(Y) \ln ( \frac{n_{ij}}{n_{i \cdot}} ) + (H(X) - H(XY)) \ln ( \frac{n_{\cdot j}}n ) )^2$

where

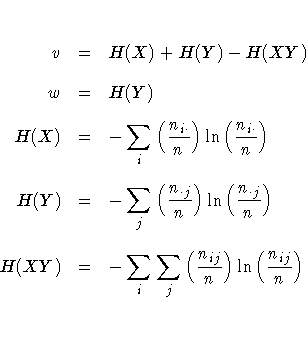
$v & = & H(X) + H(Y) - H(XY) \ w & = & H(Y) \ H(X) & = & -\sum_i ( \frac{n_{i \... ...}n ) \ H(XY) & = & -\sum_i \sum_j ( \frac{n_{ij}}n ) \ln ( \frac{n_{ij}}n ) \$

Refer to Theil (1972, pp. 115 -120) and Goodman and Kruskal (1979).

Uncertainty Coefficient (U )

The uncertainty coefficient, U, is the symmetric version of the two asymmetric coefficients. It has the range $0 \leq U \leq 1$ . It is defined as

U = [( 2(H(X) + H(Y) - H(XY)) )/( H(X) + H(Y) )]

with

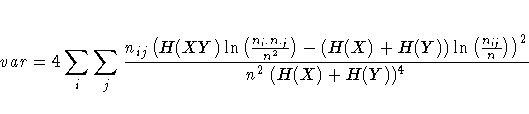
$var = 4 \sum_i \sum_j \frac{ n_{ij} ( H(XY) \ln ( \frac{n_{i \cdot} n_{\c... ... ) - (H(X) + H(Y)) \ln ( \frac{n_{ij}}n ) )^2 } {n^2 (H(X) + H(Y))^4}$

Refer to Goodman and Kruskal (1979).

Chapter Contents
Previous
Next
Top