Exact Statistics

The FREQ Procedure

Exact Statistics

Exact statistics can be useful in situations where the asymptotic assumptions are not met, and so the asymptotic p-values are not close approximations for the true p-values. Standard asymptotic methods involve the assumption that the test statistic follows a particular distribution when the sample size is sufficiently large. When the sample size is not large, asymptotic results may not be valid, with the asymptotic p-values differing perhaps substantially from the exact p-values. Asymptotic results may also be unreliable when the distribution of the data is sparse, skewed, or heavily tied. Refer to Agresti (1996) and Bishop, Fienberg, and Holland (1975). Exact computations are based on the statistical theory of exact conditional inference for contingency tables, reviewed by Agresti (1992).

In addition to computation of exact p-values, PROC FREQ provides the option of estimating exact p-values by Monte Carlo simulation. This can be useful for problems that are so large that exact computations require a great amount of time and memory, but for which asymptotic approximations may not be sufficient.

PROC FREQ provides exact p-values for the following tests for two-way tables: Pearson chi-square, likelihood-ratio chi-square, Mantel-Haenszel chi-square, Fisher's exact test, Jonckheere-Terpstra test, Cochran-Armitage test for trend, and McNemar's test. PROC FREQ also computes exact p-values for tests of hypotheses that the following statistics equal zero: Pearson correlation coefficient, Spearman correlation coefficient, simple kappa coefficient, and weighted kappa coefficient. Additionally, PROC FREQ computes exact confidence limits for the odds ratio for 2 × 2 tables. For one-way frequency tables, PROC FREQ provides the exact chi-square goodness-of-fit test (for equal proportions or for proportions or frequencies that you specify). Also for one-way tables, PROC FREQ provides exact confidence limits for the binomial proportion and an exact test for the binomial proportion value.

The following sections summarize the exact computational algorithms, define the exact p-values that PROC FREQ computes, discuss the computational resource requirements, and describe the Monte Carlo estimation option.

Computational Algorithms

PROC FREQ computes exact p-values for general R ×C tables using the network algorithm developed by Mehta and Patel (1983). This algorithm provides a substantial advantage over direct enumeration, which can be very time-consuming and feasible only for small problems. Refer to Agresti (1992) for a review of algorithms for computation of exact p-values, and refer to Mehta, Patel, and Tsiatis (1984) and Mehta, Patel, and Senchaudhuri (1991) for information on the performance of the network algorithm.

The reference set for a given contingency table is the set of all contingency tables with the observed marginal row and column sums. Corresponding to this reference set, the network algorithm forms a directed acyclic network consisting of nodes in a number of stages. A path through the network corresponds to a distinct table in the reference set. The distances between nodes are defined so that the total distance of a path through the network is the corresponding value of the test statistic. At each node, the algorithm computes the shortest and longest path distances for all the paths that pass through that node. For statistics that can be expressed as a linear combination of cell frequencies multiplied by increasing row and column scores, PROC FREQ computes shortest and longest path distances using the algorithm given in Agresti, Mehta, and Patel (1990). For statistics of other forms, PROC FREQ computes an upper bound for the longest path and a lower bound for the shortest path, following the approach of Valz and Thompson (1994).

The longest and shortest path distances or bounds for a node are compared to the value of the test statistic to determine whether all paths through the node contribute to the p-value, none of the paths through the node contribute to the p-value, or neither of these situations occur. If all paths through the node contribute, the p-value is incremented accordingly, and these paths are eliminated from further analysis. If no paths contribute, these paths are eliminated from the analysis. Otherwise, the algorithm continues, still processing this node and the associated paths. The algorithm finishes when all nodes have been accounted for, incrementing the p-value accordingly, or eliminated.

In applying the network algorithm, PROC FREQ uses full precision to represent all statistics, row and column scores, and other quantities involved in the computations. Although it is possible to use rounding to improve the speed and memory requirements of the algorithm, PROC FREQ does not do this since it can result in reduced accuracy of the p-values.

PROC FREQ computes exact confidence limits for the odds ratio according to an iterative algorithm based on that presented by Thomas (1971). Refer also to Gart (1971). Because this is a discrete problem, the confidence coefficient is not exactly $1-\alpha$ , but it is at least $1-\alpha$ . Thus, these confidence limits are conservative.

For one-way tables, PROC FREQ computes the exact chi-square goodness-of-fit test by the method of Radlow and Alf (1975). PROC FREQ generates all possible one-way tables with the observed total sample size and number of categories. For each possible table, PROC FREQ compares its chi-square value with the value for the observed table. If the table's chi-square value is greater than or equal to the observed chi-square, PROC FREQ increments the exact p-value by the probability of that table, which is calculated under the null hypothesis using the multinomial frequency distribution. By default, the null hypothesis states that all categories have equal proportions. If you specify null hypothesis proportions or frequencies using the TESTP= or TESTF= option in the TABLES statement, then PROC FREQ calculates the exact chi-square test based on that null hypothesis.

For binomial proportions in one-way tables, PROC FREQ computes exact confidence limits using the F distribution method given in Collett (1991) and also described by Leemis and Trivedi (1996). PROC FREQ computes the exact test for a binomial proportion (H0: p = p₀) by summing binomial probabilities over all alternatives. See the section "Binomial Proportion" for details. By default, PROC FREQ uses p₀ = 0.5 as the null hypothesis proportion. Alternatively, you can specify the null hypothesis proportion with the P= option in the TABLES statement.

Definition of p-Values

For several tests in PROC FREQ, the test statistic is nonnegative, and large values of the test statistic indicate a departure from the null hypothesis. Such tests include Pearson's chi-square, the likelihood-ratio chi-square, the Mantel-Haenszel chi-square, Fisher's exact test for tables larger than 2 × 2 tables, McNemar's test, and the one-way chi-square goodness-of-fit test. The exact p-value for these nondirectional tests is the sum of probabilities for those tables having a test statistic greater than or equal to the value of the observed test statistic.

There are other tests where it may be appropriate to test against either a one-sided or a two-sided alternative hypothesis. For example, when you test the null hypothesis that the true parameter value equals 0 (T = 0), the alternative of interest may be one-sided ( $T \leq 0$ , or $T \geq 0$ ) or two-sided ( $T \neq 0$ ). Such tests include the Pearson correlation coefficient, Spearman correlation coefficient, Jonckheere-Terpstra test, Cochran-Armitage test for trend, simple kappa coefficient, and weighted kappa coefficient. For these tests, PROC FREQ outputs the right-sided p-value when the observed value of the test statistic is greater than its expected value. The right-sided p-value is the sum of probabilities for those tables having a test statistic greater than or equal to the observed test statistic. Otherwise, when the test statistic is less than or equal to its expected value, PROC FREQ outputs the left-sided p-value. The left-sided p-value is the sum of probabilities for those tables having a test statistic less than or equal to the one observed. The one-sided p-value P₁ can be expressed as

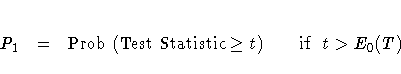
$P_{1} = {\rm Prob} ({\rm TestStatistic} \geq t) {\rm if} t \gt E_{0}(T)$

$P_{1} = {\rm Prob} ({\rm TestStatistic} \leq t) {\rm if} t \leq E_{0}(T)$

where t is the observed value of the test statistic and E₀(T) is the expected value of the test statistic under the null hypothesis. PROC FREQ computes the two-sided p-value as the sum of the one-sided p-value and the corresponding area in the opposite tail of the distribution of the statistic, equidistant from the expected value. The two-sided p-value P₂ can be expressed as

$P_{2} = {\rm Prob} ( | {\rm TestStatistic} - E_{0}(T) | \geq | t - E_{0}(T) | )$

Computational Resources

PROC FREQ uses relatively fast and efficient algorithms for exact computations. These recently developed algorithms, together with improvements in computer power, make it feasible now to perform exact computations for data sets where previously only asymptotic methods could be applied. Nevertheless, there are still large problems that may require a prohibitive amount of time and memory for exact computations, depending on the speed and memory available on your computer. For large problems, consider whether exact methods are really needed or whether asymptotic methods might give results quite close to the exact results, while requiring much less computer time and memory. When asymptotic methods may not be sufficient for such large problems, consider using Monte Carlo estimation of exact p-values, as described in the "Monte Carlo Estimation" section.

A formula does not exist that can predict in advance how much time and memory are needed to compute an exact p-value for a certain problem. The time and memory required depend on several factors, including which test is being performed, the total sample size, the number of rows and columns, and the specific arrangement of the observations into table cells. Generally, larger problems (in terms of total sample size, number of rows, and number of columns) tend to require more time and memory. Additionally, for a fixed total sample size, time and memory requirements tend to increase as the number of rows and columns increases, since this corresponds to an increase in the number of tables in the reference set. Also for a fixed sample size, time and memory requirements increase as the marginal row and column totals become more homogeneous. Refer to Agresti, Mehta, and Patel (1990) and Gail and Mantel (1977).

At any time while PROC FREQ is computing exact p-values, you can terminate the computations by pressing the system interrupt key sequence (refer to the SAS Companion for your system) and choosing to stop computations. After you terminate exact computations, PROC FREQ completes all other remaining tasks. The procedure produces the requested output and reports missing values for any exact p-values that were not computed by the time of termination.

You can also use the MAXTIME= option in the EXACT statement to limit the amount of time PROC FREQ uses for exact computations. You specify a MAXTIME= value that is the maximum amount of clock time (in seconds) that PROC FREQ can use to compute an exact p-value. If PROC FREQ does not finish computing an exact p-value within that time, it terminates the computation and completes all other remaining tasks.

Monte Carlo Estimation

If you specify the option MC in the EXACT statement, PROC FREQ computes Monte Carlo estimates of the exact p-values instead of directly computing the exact p-values. Monte Carlo estimation can be useful for large problems that require a great amount of time and memory for exact computations but for which asymptotic approximations may not be sufficient. To describe the precision of each Monte Carlo estimate, PROC FREQ provides the asymptotic standard error and $100(1 - \alpha)$ % confidence limits. The confidence level $\alpha$ is determined by the ALPHA= option in the EXACT statement, which, by default, equals 0.01, and produces 99% confidence limits. The N=n option in the EXACT statement specifies the number of samples that PROC FREQ uses for Monte Carlo estimation; the default is 10000 samples. You can specify a larger value for n to improve the precision of the Monte Carlo estimates. Because larger values of n generate more samples, the computation time increases. Alternatively, you can specify a smaller value of n to reduce the computation time.

To compute a Monte Carlo estimate of an exact p-value, PROC FREQ generates a random sample of tables with the same total sample size, row totals, and column totals as the observed table. PROC FREQ uses the algorithm of Agresti, Wackerly, and Boyett (1979), which generates tables in proportion to their hypergeometric probabilities conditional on the marginal frequencies. For each sample table, PROC FREQ computes the value of the test statistic and compares it to the value for the observed table. When estimating a right-sided p-value, PROC FREQ counts all sample tables for which the test statistic is greater than or equal to the observed test statistic. Then the p-value estimate equals the number of these tables divided by the total number of tables sampled.

$\hat{P}_{{\small MC}} & = & M / N \ M & = & {number of samples with} ({Test ... ...geq t) \ N & = & {total number of samples} \ t & = & {observed Test Statistic} \$

PROC FREQ computes left-sided and two-sided p-value estimates in a similar manner. For left-sided p-values, PROC FREQ evaluates whether the test statistic for each sampled table is less than or equal to the observed test statistic. For two-sided p-values, PROC FREQ examines the sample test statistics according to the expression for P₂ given in the "Asymptotic Tests" section. The variable M is a binomially distributed variable with N trials and success probability p. It follows that the asymptotic standard error of the Monte Carlo estimate is

$se(\hat{P}_{{\small MC}}) = \sqrt{\hat{P}_{{\small MC}} ( 1 - \hat{P}_{{\small MC}}) / (N-1) }$

PROC FREQ constructs asymptotic confidence limits for the p-values according to

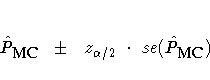
$\hat{P}_{{\small MC}}\pmz_{\alpha/2} \cdot se(\hat{P}_{{\small MC}})$

where $z_{\alpha/2}$ is the $100(1 - \alpha/2)$ percentile of the standard normal distribution, and the confidence level $\alpha$ is determined by the ALPHA= option in the EXACT statement.

When the Monte Carlo estimate $\hat{P}_{{\small MC}}$ equals 0, then PROC FREQ computes the confidence limits for the p-value as

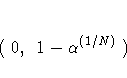
$( 0, 1 - \alpha^{(1/N)} )$

When the Monte Carlo estimate $\hat{P}_{MC}$ equals 1, then PROC FREQ computes the confidence limits as

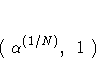
$( \alpha^{(1/N)}, 1 )$

Chapter Contents
Previous
Next
Top