Chapter Contents

Previous

Next

Solving Standard Least-Squares Problems

This section illustrates how to solve some ordinary least-squares problems and generalizations of those problems by formulating them as transformation regression problems. One problem involves finding linear and nonlinear regression functions in a scatter plot. The next problem involves simultaneously fitting two lines or curves through a scatter plot. The last problem involves finding the overall fit of a multi-way main-effects and interactions analysis-of-variance model.

Nonlinear Regression Functions

   proc transreg;
      model identity(y) = identity(x);
      output predicted;
   run;

A monotone regression function (in this case, a monotonically decreasing regression function, since the correlation coefficient is negative) can be found by requesting an MSPLINE transformation of the independent variable, as follows.

   proc transreg;
      model identity(y) = mspline(x / nknots=9);
      output predicted;
   run;

The monotonicity restriction can be relaxed by requesting a SPLINE transformation of the independent variable, as shown below.

   proc transreg;
      model identity(y) = spline(x / nknots=9);
      output predicted;
   run;

In this example, it is not useful to plot the transformation TX, since TX is just an intermediate result used in finding a regression function through the original X and Y scatter plot.

The following statements provide a specific example of using the TRANSREG procedure for fitting nonlinear regression functions. These statements produce Figure 65.15 through Figure 65.18.

   title 'Linear and Nonlinear Regression Functions';
   *---Generate an Artificial Nonlinear Scatter Plot---;
   *---SAS/IML Software is Required for this Example---;
   proc iml;
      N   = 500;
      X   = (1:N)`;
      X   = X/(N/200);
      Y   = -((X/50)-1.5)##2 + sin(X/8) + sqrt(X)/5 + 2*log(X) + cos(X);
      X   = X - X[:,];
      X   = -X / sqrt(X[##,]/(n-1));
      Y   = Y - Y[:,];
      Y   = Y / sqrt(Y[##,]/(n-1));
      all = Y || X;
      create outset from all;
      append        from all;
      quit;

   data A;
      set outset(rename=(col1=Y col2=X));
      if Y<-2 then Y=-2 + ranuni(7654321)/2;
      X1=X; X2=X; X3=X; X4=X;
   run;

   *---Predicted Values for the Linear Regression Line---;
   proc transreg data=A;
      title2 'A Linear Regression Line';
      model identity(Y)=identity(X);
      output out=A pprefix=L;
      id X1-X4;
   run;

   *---Predicted Values for the Monotone Regression Function---;
   proc transreg data=A;
      title2 'A Monotone Regression Function';
      model identity(Y)=mspline(X / nknots=9);
      output out=A pprefix=M;
      id X1-X4 LY;
   run;

   *---Predicted Values for the Nonmonotone Regression Function---;
   proc transreg data=A;
      title2 'A Nonmonotone Regression Function';
      model identity(Y)=spline(X / nknots=9);
      output out=A predicted;
      id X1-X4 LY MY;
   run;

   *---Plot the Results---;
   goptions goutmode=replace nodisplay;
   %let opts = haxis=axis2 vaxis=axis1 frame cframe=ligr;
   * Depending on your goptions, these plot options may work better:
   * %let opts = haxis=axis2 vaxis=axis1 frame;

   proc gplot data=A;
      title;
      axis1 minor=none label=(angle=90 rotate=0)
            order=(-2 to 2 by 2);
      axis2 minor=none order=(-2 to 2 by 2);
      plot Y*X1=1         /         &opts name='tregnl1';
      plot Y*X2=1 LY*X2=2 / overlay &opts name='tregnl2';
      plot Y*X3=1 MY*X3=2 / overlay &opts name='tregnl3';
      plot Y*X4=1 PY*X4=2 / overlay &opts name='tregnl4';
      symbol1 color=blue   v=star i=none;
      symbol2 color=yellow v=none i=join;
      label X1 = 'Nonlinear Scatter Plot'
            X2 = 'Linear Regression, r**2 = 0.14580'
            X3 = 'Monotone Function, r**2 = 0.60576'
            X4 = 'Nonlinear Function, r**2 = 0.89634';
   run; quit;

   goptions display;
   proc greplay nofs tc=sashelp.templt template=l2r2;
      igout gseg;
      treplay 1:tregnl1 2:tregnl3 3:tregnl2 4:tregnl4;
   run; quit;

The squared correlation is only 0.15 for the linear regression, showing that a simple linear regression model is not appropriate for these data. By relaxing the constraints placed on the regression line, the proportion of variance accounted for increases from 0.15 (linear) to 0.61 (monotone) to 0.90 (nonmonotone). Relaxing the linearity constraint allows the regression function to bend and more closely follow the right portion of the scatter plot. Relaxing the monotonicity constraint allows the regression function to follow the periodic portion of the left side of the plot more closely. The nonlinear MSPLINE transformation is a quadratic spline with knots at the deciles. The nonlinear nonmonotonic SPLINE transformation is a cubic spline with knots at the deciles.

Different knots and different degrees would produce slightly different results. The two nonlinear regression functions could be closely approximated by simpler piecewise linear regression functions. The monotone function could be approximated by a two-piece line with a single knot at the elbow. The nonmonotone function could be approximated by a six-piece function with knots at the five elbows.

With this type of problem (one dependent variable with no missing values that is not transformed and one independent variable that is nonlinearly transformed), PROC TRANSREG always iterates exactly twice (although only one iteration is necessary). The first iteration reports the R² for the linear regression line and finds the optimal transformation of X. Since the data change in the first iteration, a second iteration is performed, which reports the R² for the final nonlinear regression function, and zero data change. The predicted values, which are a linear function of the optimal transformation of X, contain the y-coordinates for the nonlinear regression function. The variance of the predicted values divided by the variance of Y is the R² for the fit of the nonlinear regression function. When X is monotonically transformed, the transformation of X is always monotonically increasing, but the predicted values increase if the correlation is positive and decrease for negative correlations.

Simultaneously Fitting Two Regression Functions

   proc transreg data=A dummy;
      title 'Parallel Lines, Separate Intercepts';
      model identity(Y)=class(G) identity(X);
      output predicted;
   run;

   proc transreg data=A;
      title 'Parallel Monotone Curves, Separate Intercepts';
      model identity(Y)=class(G) mspline(X / knots=-1.5 to 2.5 by 0.5);
      output predicted;
   run;

   proc transreg data=A dummy;
      title 'Parallel Curves, Separate Intercepts';
      model identity(Y)=class(G) spline(X / knots=-1.5 to 2.5 by 0.5);
      output predicted;
   run;

   proc transreg data=A;
      title 'Separate Slopes, Same Intercept';
      model identity(Y)=class(G / zero=none) * identity(X);
      output predicted;
   run;

   proc transreg data=A;
      title 'Separate Monotone Curves, Same Intercept';
      model identity(Y) = class(G / zero=none) *
                          mspline(X / knots=-1.5 to 2.5 by 0.5);
      output predicted;
   run;

   proc transreg data=A dummy;
      title 'Separate Curves, Same Intercept';
      model identity(Y) = class(G / zero=none) *
                          spline(X / knots=-1.5 to 2.5 by 0.5);
      output predicted;
   run;

   proc transreg data=A;
      title 'Separate Slopes, Separate Intercepts';
      model identity(Y) = class(G / zero=none) | identity(X);
      output predicted;
   run;

   proc transreg data=A;
      title 'Separate Monotone Curves, Separate Intercepts';
      model identity(Y) = class(G / zero=none) |
                          mspline(X / knots=-1.5 to 2.5 by 0.5);
      output predicted;
   run;

   proc transreg data=A dummy;
      title 'Separate Curves, Separate Intercepts';
      model identity(Y) = class(G / zero=none) |
                          spline(X / knots=-1.5 to 2.5 by 0.5);
      output predicted;
   run;

Since the variables X1 and X2 both have a large partition of zeros, the KNOTS= t-option is specified instead of the NKNOTS= t-option. The following example generates an artificial data set with two curves. In the interest of space, only the preceding separate curves, separate intercepts example is run.

   title 'Separate Curves, Separate Intercepts';

   data A;
      do X = -2 to 3 by 0.025;
         G = 1;
         Y = 8*(X*X + 2*cos(X*6)) + 15*normal(7654321);
         output;
         G = 2;
         Y = 4*(-X*X + 4*sin(X*4)) - 40 + 15*normal(7654321);
         output;
         end;
   run;

   proc transreg data=A dummy;
      model identity(Y) = class(G / zero=none) |
                          spline(X / knots=-1.5 to 2.5 by 0.5);
      output predicted;
   run;

   proc gplot;
      axis1 minor=none;
      axis2 minor=none label=(angle=90 rotate=0);
      symbol1 color=blue   v=star i=none;
      symbol2 color=yellow v=dot  i=none;
      plot Y*X=1 PY*X=2 /overlay frame cframe=ligr haxis=axis1 
                         vaxis=axis2 HREF=0 vref=0;
   run; quit;

The previous statements produce Figure 65.19 through Figure 65.20.

Unbalanced ANOVA without Dummy Variables

Finding the overall fit of a large, unbalanced analysis of variance model can be handled as an optimal scoring problem without creating large, sparse design matrices. For example, consider an unbalanced full main-effects and interactions ANOVA model with six factors. Assume that a SAS data set is created with factor level indicator variables C1 through C6 and dependent variable Y. If each factor level consists of nonblank single characters, you can create a cell indicator in a DATA step with the statement

   x=compress(c1||c2||c3||c4||c5||c6);

The following statements optimally score X (using the OPSCORE transformation) and do not transform Y. The final R² reported is the R² for the full analysis of variance model.

   proc transreg;
      model identity(y)=opscore(x);
      output;
   run;

The R² displayed by the preceding statements is the same as the R² that would be reported by both of the following PROC GLM runs.

   proc glm;
      class x;
      model y=x;
   run;

   proc glm;
      class c1-c6;
      model y=c1|c2|c3|c4|c5|c6;
   run;

PROC TRANSREG optimally scores the classes of X, within the space of a single variable with values linearly related to the cell means, so the full ANOVA problem is reduced to a simple regression problem with an optimal independent variable. PROC TRANSREG requires only one iteration to find the optimal scoring of X but, by default, performs a second iteration, which reports no data changes.

Hypothesis Tests for Simple Univariate Models

   data htex;
      do i = 0.5 to 10 by 0.5;
         x1 = log(i);
         x2 = sqrt(i) + sin(i);
         x3 = 0.05 * i * i + cos(i);
         y  = x1 - x2 + x3 + 3 * normal(7);
         x1 = x1 + normal(7);
         x2 = x2 + normal(7);
         x3 = x3 + normal(7);
         output;
      end;
   run;

Both PROC TRANSREG and PROC REG are run to fit the same polynomial regression model. The ANOVA and regression tables from PROC TRANSREG are displayed in Figure 65.21. The ANOVA and regression tables from PROC REG are displayed in Figure 65.22. The SHORT a-option is specified to suppress the iteration history.

   proc transreg data=htex ss2 short;
      title 'Fit a Polynomial Regression Model with PROC TRANSREG';
      model identity(y) = spline(x1);
   run;

   data htex2;
      set htex;
      x1_1 = x1;
      x1_2 = x1 * x1;
      x1_3 = x1 * x1 * x1;
   run;

   proc reg;
      title 'Fit a Polynomial Regression Model with PROC REG';
      model y = x1_1 - x1_3;
   run;

The PROC TRANSREG regression table differs in several important ways from the parameter estimate table produced by PROC REG. The REG procedure displays standard errors and ts. PROC TRANSREG displays Type II sums of squares, mean squares, and Fs. The difference is because the numerator degrees of freedom are not always 1, so t-tests are not uniformly appropriate. When the degrees of freedom for variable x_j is 1, the following relationships hold between the standard errors and the Type II sums of squares (SS_j):

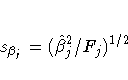
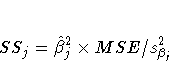
PROC TRANSREG does not provide tests of the individual terms that go into the transformation. (However it could if BSPLINE or PSPLINE had been specified instead of SPLINE.) The test of SPLINE(X1) is the same as the test of the overall model. The intercepts are different due to the different numbers of variables and their standardizations.

In the next example, both X1 and X2 are transformed in the first PROC TRANSREG step, and PROC TRANSREG is used instead of a DATA step to create the polynomials for PROC REG. Both PROC TRANSREG and PROC REG fit the same polynomial regression model. The output from PROC TRANSREG is in Figure 65.23. The output from PROC REG is in Figure 65.24.

   proc transreg data=htex ss2 dummy;
      title 'Two-Variable Polynomial Regression';
      model identity(y) = spline(x1 x2);
   run;

   proc transreg noprint data=htex maxiter=0;
      /* Use PROC TRANSREG to prepare input to PROC REG */
      model identity(y) = pspline(x1 x2);
      output out=htex2;
   run;

   proc reg;
      model y = x1_1-x1_3 x2_1-x2_3;
      test x1_1, x1_2, x1_3;
      test x2_1, x2_2, x2_3;
   run;

   model identity(y) = spline(x2);

which excludes SPLINE(X1). The third is for

   model identity(y) = spline(x1);

which excludes SPLINE(X2). The difference between the first and second R² times the total sum of squares is the model sum of squares for SPLINE(X1)

(0.17287 - 0.15249) ×224.143800 = 4.568165

(0.17287 - 0.02604) ×224.143800 = 32.911247

Hypothesis Tests with Monotonicity Constraints

   proc transreg data=htex ss2 short;
      title 'Monotone Splines';
      model identity(y) = mspline(x1-x3 / nknots=3);
   run;

The SHORT a-option is specified to suppress the iteration histories. Two ANOVA tables are displayed -one using liberal degrees of freedom and one using conservative degrees of freedom. All sums of squares and the R²s are the same for both tables. What differs are the degrees of freedom and statistics that are computed using degrees of freedom. The liberal test has 8 model degrees of freedom and 11 error degrees of freedom, whereas the conservative test has 15 model degrees of freedom and only 4 error degrees of freedom. The "true" p-value is between 0.8462 and 0.9997, so clearly you would fail to reject the null hypothesis. Unfortunately, results are not always this clear. See Figure 65.25.

Hypothesis Tests with Dependent Variable Transformations

The second difference concerns the usual multivariate test statistics: Pillai's Trace, Wilks' Lambda, Hotelling-Lawley Trace, and Roy's Greatest Root. The first three statistics are defined in terms of all the squared canonical correlations. Here, there is only one linear combination (the transformation) and, hence, only one squared canonical correlation of interest, which is equal to the R². It may seem that Roy's Greatest Root, which uses only the largest squared canonical correlation, is the only statistic of interest. Unfortunately, Roy's Greatest Root is very liberal and provides only a lower bound on the p-value. Approximate upper bounds are provided by adjusting the other three statistics for the one linear combination case. The Wilks' Lambda, Pillai's Trace, and Hotelling-Lawley Trace statistics are a conservative adjustment of the usual statistics.

These statistics are normally defined in terms of the squared canonical correlations, which are the eigenvalues of the matrix H (H+E)^-1, where H is the hypothesis sum-of-squares matrix and E is the error sum-of-squares matrix. Here the R² is used for the first eigenvalue, and all other eigenvalues are set to 0 since only one linear combination is used. Degrees of freedom are computed assuming that all linear combinations contribute to the Lambda and Trace statistics, so the F tests for those statistics are conservative. The p-values for the liberal and conservative statistics provide approximate lower and upper bounds on p. In practice, the adjusted Pillai's Trace is very conservative -perhaps too conservative to be useful. Wilks' Lambda is less conservative, and the Hotelling-Lawley Trace seems to be the least conservative. The conservative statistics and the liberal Roy's Greatest Root provide a bound on the true p-value. Unfortunately, they sometimes report a bound of 0.0001 and 1.0000.

Here is an example with a dependent variable transformation.

   proc transreg data=htex ss2 dummy short;
      title 'Transform Dependent and Independent Variables';
      model spline(y) = spline(x1-x3);
   run;

The univariate results match Roy's Greatest Root results. Clearly, the proper action is to fail to reject the null hypothesis. However, as stated previously, results are not always this clear. See Figure 65.26.

Hypothesis Tests with One-Way ANOVA

   data oneway;
      input y x $;
      datalines;
   0 a
   1 a
   2 a
   7 b
   8 b
   9 b
   3 c
   4 c
   5 c
   ;

   proc transreg ss2 data=oneway short;
      title 'Implicit Intercept Model';
      model identity(y) = class(x / zero=none);
      output out=oneway2;
   run;

   proc reg data=oneway2;
      model y = xa xb xc;         /* Implicit Intercept ANOVA      */
      model y = xa xb xc / noint; /* Implicit Intercept Regression */
   run;

Chapter Contents

Previous

Next

Top

Copyright © 1999 by SAS Institute Inc., Cary, NC, USA. All rights reserved.