Postscript version of this page

STAT 450 Lecture 2

Change of variables

Reading for Today's Lecture: Sections 1 to 3 of Chapter 4 of Mood, Graybill and Boes.

Goals of Today's Lecture:

• Show some examples of cdfs and densities.

• Introduce the idea of distribution theory.

Today's notes

Last time: We defined Probability Space $(\Omega,{\cal F},P)$, real and R^p valued random variables, cumulative distribution functions, $F_X(x) =P(X\le x)$, described properties of Ffor p=1 and proved a couple of these facts about F.

Definition: The distribution of a random variable X is discrete (we also call the random variable discrete) if there is a countable set $x_1,x_2,\cdots$ such that

$$P(X \in \{ x_1,x_2 \cdots\}) =1 = \sum_i P(X=x_i)$$

In this case the discrete density or probability mass function of X is

f_X(x) = P(X=x)

The distribution of a random variable X is absolutely continuous if there is a function f such that

$$P(X\in A) = \int_A f(x) dx$$

for any set A. This is a p dimensional integral in general. This condition is equivalent (for p=1) to

$$F(x) = \int_{-\infty}^x f(y) \, dy$$

We call f the density of X. For most values of x we then have F is differentiable at x and (for p=1)

$$F^\prime(x) =f(x) \, .$$

Notation: Some students will not be used to the notation $\int_A f(x) dx$ for a multiple integral. For instance if p=2 and the set A is the disk of radius 1 centered at the origin then

$$\int_A f(x) dx \equiv \int_{-1}^1 \int_{-\sqrt{1-x_1^2}}^{\sqrt{1-x_1^2}} f(x_1,x_2) \, dx_2 \, dx_1$$

Example: X is exponential.

$$F(x) = \left\{ \begin{array}{ll} 1- e^{-x} & x > 0 \\ 0 & x \le 0 \end{array}\right.$$

$$f(x) = \left\{ \begin{array}{ll} e^{-x} & x> 0 \\ \mbox{undefined} & x= 0 \\ 0 & x < 0 \end{array}\right.$$

Example: The function

$$f(u,v) = \begin{cases} u+v & 0 < u,v < 1 \\ 0 & \text{otherwise} \end{cases}$$

is a density. The corresponding cdf is

$$F(x,y) = \begin{cases} 0 & x\le 0 \text{ or } y\le 0 \\ xy(x... ... x \ge 1 \text{ and } 0 < y < 1 \\ 1 & x,y \ge 1 \end{cases}$$

Distribution Theory

General Problem: Start with assumptions (the very important process of thinking up these assumptions for a real problem is called modelling) about the density or CDF of a random vector $X=(X_1,\ldots,X_p)$. Define $Y=g(X_1,\ldots,X_p)$ to be some function of X (usually some statistic of interest). How can we compute the distribution or CDF or density of Y?

Univariate Techniques

Method 1: compute the CDF by integration and differentiate to find f_Y.

Example: $U \sim \mbox{Uniform}[0,1]$ and $Y=-\log U$. Then

$$\begin{eqnarray*}F_Y(y) & = & P(Y \le y) = P(-\log U \le y) \\ & = & P(\log U ... ...{array}{ll} 1- e^{-y} & y > 0 \\ 0 & y \le 0 \end{array}\right. \end{eqnarray*}$$

so that Y has a standard exponential distribution.

Example: $Z \sim N(0,1)$, i.e.

$$f_Z(z) = \frac{1}{\sqrt{2\pi}} e^{-z^2/2}$$

and Y=Z². Then

$$F_Y(y) = P(Z^2 \le y) = \left\{ \begin{array}{ll} 0 & y < ... ... P(-\sqrt{y} \le Z \le \sqrt{y}) & y \ge 0 \end{array}\right.$$

Now

$$P(-\sqrt{y} \le Z \le \sqrt{y}) = F_Z(\sqrt{y}) -F_Z(-\sqrt{y})$$

can be differentiated to obtain

$$f_Y(y) = \left\{ \begin{array}{ll} 0 & y < 0 \\ \frac{d}{dy... ...\right] & y > 0 \\ \mbox{undefined} & y=0 \end{array}\right.$$

Then

$$\begin{eqnarray*}\frac{d}{dy} F_Z(\sqrt{y}) & = & f_Z(\sqrt{y})\frac{d}{dy}\sqrt... ...frac{1}{2} y^{-1/2} \\ & = & \frac{1}{2\sqrt{2\pi y}} e^{-y/2} \end{eqnarray*}$$

with a similar formula for the other derivative. Thus

$$f_Y(y) = \left\{ \begin{array}{ll} \frac{1}{\sqrt{2\pi y}} e... ...0 \\ 0 & y < 0 \\ \mbox{undefined} & y=0 \end{array}\right.$$

We will find indicator notation useful:

$$1(y>0) = \left\{ \begin{array}{ll} 1 & y>0 \\ 0 & y \le 0 \end{array}\right.$$

which we use to write

$$f_Y(y) = \frac{1}{\sqrt{2\pi y}} e^{-y/2} 1(y>0)$$

(changing the definition unimportantly at y=0).

Notice: I never evaluated F_Y before differentiating it. In fact F_Y and F_Z are integrals I can't do but I can differentiate then anyway. You should remember the fundamental theorem of calculus:

$$\frac{d}{dx} \int_a^x f(y) \, dy = f(x)$$

at any x where f is continuous.

Method 2: Change of variables.

Now assume g is one to one. I will do the case where g is increasing and I will be assuming that g is differentiable. The density has the following interpretation (mathematically what follows is just the expression of the fact that the density is the derivative of the cdf):

$$f_Y(y) = \lim_{\delta y \to 0} \frac{P(y \le Y \le y+\delta y... ... \lim_{\delta y \to 0} \frac{F_Y(y+\delta y)-F_Y(y)}{\delta y}$$

and

$$f_X(x) = \lim_{\delta x \to 0} \frac{P(x \le X \le x+\delta x)}{\delta x}$$

Now assume that y=g(x). Then

$$P( y \le Y \le g(x+\delta x) ) = P( x \le X \le x+\delta x)$$

Each of these probabilities is the integral of a density. The first is the integral of the density of Y over the small interval from y=g(x) to $y=g(x+\delta x)$. Since the interval is narrow the function f_Y is nearly constant over this interval and we get

$$P( y \le Y \le g(x+\delta x) ) \approx f_Y(y)(g(x+\delta x) - g(x))$$

Since g has a derivative the difference

$$g(x+\delta x) - g(x) \approx \delta x g^\prime(x)$$

and we get

$$P( y \le Y \le g(x+\delta x) ) \approx f_Y(y) g^\prime(x) \delta x$$

On the other hand the same idea applied to the probability expressed in terms of X gives

$$P( x \le X \le x+\delta x) \approx f_X(x) \delta x$$

which gives

$$f_Y(y) g^\prime(x) \delta x \approx f_X(x) \delta x$$

or, cancelling the $\delta x$ in the limit

$$f_Y(y) g^\prime(x) = f_X(x)$$

If you remember y=g(x) then you get

$$f_X(x) = f_Y(g(x)) g^\prime(x)$$

or if you solve the equation y=g(x) to get x in terms of y, that is, x=g^-1(y) then you get the usual formula

$$f_Y(y) = f_X(g^{-1}(y)) / g^\prime(g^{-1}(y))$$

I find it easier to remember the first of these formulas. This is just the change of variables formula for doing integrals.

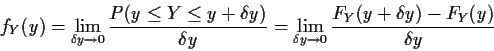
Remark: If g had been decreasing the derivative $g^\prime$ would have been negative but in the argument above the interval $(g(x), g(x+\delta x))$would have to have been written in the other order. This would have meant that our formula had $g(x) - g(x+\delta x) \approx -g^\prime(x) \delta x$. In both cases this amounts to the formula

$$f_X(x) = f_Y(g(x))\vert g^\prime(x)\vert \, .$$

The quantity $\vert g^\prime(x)\vert$ is called the Jacobian of the transformation g.

Example: $X\sim\mbox{Weibull(shape $\alpha$ , scale $\beta$ )}$or (see Chapter 3 for definitions of a number of ``standard'' distributions)

$$f_X(x)= \frac{\alpha}{\beta} \left(\frac{x}{\beta}\right)^{\alpha-1} \exp\left\{ -(x/\beta)^\alpha\right\} 1(x>0)$$

Let $Y=\log X$ so that $g(x) = \log(x)$. Setting $y=\log x$ and solving gives $x=\exp(y)$ so that g^-1(y) = e^y. Then $g^\prime(x) = 1/x$ and $1/g^\prime(g^{-1}(y)) = 1/(1/e^y) =e^y$. Hence

$$f_Y(y) = \frac{\alpha}{\beta} \left(\frac{e^y}{\beta}\right)^... ...a-1} \exp\left\{ -(e^y/\beta)^\alpha\right\} 1(e^y>0) e^y \, .$$

The indicator is always equal to 1 since e^y is always positive. Simplifying we get

$$f_Y(y) = \frac{\alpha}{\beta^\alpha} \exp\left\{\alpha y -e^{\alpha y}/\beta^\alpha\right\} \, .$$

If we define $\phi = \log\beta$ and $\theta = 1/\alpha$ then the density can be written as

$$f_Y(y) = \frac{1}{\theta} \exp\left\{\frac{y-\phi}{\theta} -\exp\left\{\frac{y-\phi}{\theta}\right\}\right\}$$

which is called an Extreme Value density with location parameter $\phi$ and scale parameter $\theta$. (Note: there are several distributions going under the name Extreme Value. If we had used $Y=-\log X$ we would have found

$$f_Y(y) = \frac{1}{\theta} \exp\left\{-\frac{y-\phi}{\theta} -\exp\left\{-\frac{y-\phi}{\theta}\right\}\right \}$$

which the book calls the Gumbel distribution.)