


Postscript version of this file
STAT 450 Lecture 3
Reading for Today's Lecture:
Sections 1, 2 and 3 of Chapter 2. Sections 1 and 2 of Chapter 4.
Goals of Today's Lecture:
- Learn how to compute density of Y=g(X) from density
of X when X and Y are real valued.
Last time: We defined:
- discrete distributions
- pmf:
f(x) = P(X=x).
- absolutely continuous rv X
- density f:
 .
.
We introduced distribution theory
- X has known distribution
- Y=g(X) -- problem is to find distribution of Y.
Method 1: Two steps:
- 1.
- Compute FY(y), the cdf of Y.
- 2.
- Find fY(y) by differentiating FY.
For Y=g(X) with X and Y each real valued
Take the derivative with respect to y to compute the density
Often we can differentiate this integral without doing the integral.
Example: :
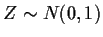 ,
i.e.
,
i.e.
and Y=Z2. Then
Now
can be differentiated to obtain
Then
with a similar formula for the other derivative. Thus
We will find indicator notation useful:
which we use to write
(changing the definition unimportantly at y=0).
Notice: I never evaluated FY before differentiating it. In fact
FY and FZ are integrals I can't do but I can differentiate then anyway.
You should remember the fundamental theorem of calculus:
at any x where f is continuous.
Method 2: Change of variables.
Now assume g is one to one.
I will do the case where g is increasing
and I will be assuming that g is differentiable.
The density has the following interpretation (mathematically
what follows is just the expression of the fact that
the density is the derivative of the cdf):
and
Now assume that y=g(x). Then
Each of these probabilities is the integral of a density. The first is the
integral of the density of Y over the small interval from y=g(x) to
 .
Since the interval is narrow the function fY is
nearly constant over this interval and we get
.
Since the interval is narrow the function fY is
nearly constant over this interval and we get
Since g has a derivative the difference
and we get
On the other hand the same idea applied to the probability expressed in terms
of X gives
which gives
or, cancelling the  in the limit
in the limit
If you remember y=g(x) then you get
or if you solve the equation y=g(x) to get x in terms of y,
that is,
x=g-1(y) then you get the usual formula
I find it easier to remember the first of these formulas.
This is just the change of variables formula for doing integrals.
Remark: If g had been decreasing the
derivative  would have been negative but in
the argument above the interval
would have been negative but in
the argument above the interval
 would have to have been written in the other order.
This would have meant that our formula had
would have to have been written in the other order.
This would have meant that our formula had
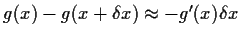 .
In both cases this amounts to the formula
.
In both cases this amounts to the formula
The quantity
 is called the Jacobian of the
transformation g.
is called the Jacobian of the
transformation g.
Example:
 or (see Chapter 3 for definitions of a number of ``standard''
distributions)
or (see Chapter 3 for definitions of a number of ``standard''
distributions)
Let  so that
so that
 .
Setting
.
Setting  and solving
gives
and solving
gives  so that
g-1(y) = ey. Then
so that
g-1(y) = ey. Then
 and
and
 .
Hence
.
Hence
The indicator is always equal to 1 since ey is always positive. Simplifying
we get
If we define
 and
and
 then the density
can be written as
then the density
can be written as
which is called an Extreme Value density with location parameter  and scale parameter
and scale parameter  .
(Note: there are several distributions going
under the name Extreme Value. If we had used
.
(Note: there are several distributions going
under the name Extreme Value. If we had used  we would have
found
we would have
found
which the book calls the Gumbel distribution.)
Marginalization
Now we turn to multivariate problems. The simplest version has
 and Y=X1 (or in general any Xj).
and Y=X1 (or in general any Xj).
Theorem 1
If
X has (joint) density

then

(with
q <
p) has a density
fY given by
We call
 the marginal density of
the marginal density of
 and use the
expression joint density for fX but
and use the
expression joint density for fX but
 is exactly the
usual density of
is exactly the
usual density of
 .
The adjective ``marginal'' is just there to
distinguish the object from the joint density of X.
.
The adjective ``marginal'' is just there to
distinguish the object from the joint density of X.
Example The function
f(x1,x2) = Kx1x21(x1> 0) 1(x2 >0) 1(x1+x2 < 1)
is a density for a suitable choice of K, namely the value of Kmaking
The integral is
so that K=24.
The marginal density of x1 is
which is the same as
This is a
 density.
density.
The general multivariate problem has
Case 1: If q>p then Y will not have a density
for ``smooth'' g. Y will have a singular or discrete distribution.
This sort of problem is rarely
of real interest. (However, variables of interest often have a
singular distribution - this is almost always true of the set of residuals
in a regression problem.)
Case 2 If q=p then we will be able to use a
change of variables
formula which generalizes the one derived above for the
case p=q=1. (See below.)
Case 3: If q < p we will try a two step process.
In the first step we pad out Y
by adding on p-q more variables (carefully chosen)
and calling them
 .
Formally we find functions
.
Formally we find functions
 and define
and define
If we have chosen the functions carefully we will find that
 satisfies the conditions for applying
the change of variables formula from the previous case.
Then we apply that case to compute fZ. Finally we marginalize
the density of Z to find that of Y:
satisfies the conditions for applying
the change of variables formula from the previous case.
Then we apply that case to compute fZ. Finally we marginalize
the density of Z to find that of Y:



Richard Lockhart
1999-09-14

![]() ,
i.e.
,
i.e.

![\begin{displaymath}f_Y(y) = \left\{ \begin{array}{ll}
0 & y < 0
\\
\frac{d}{dy...
...\right] & y > 0
\\
\mbox{undefined} & y=0
\end{array}\right.
\end{displaymath}](img9.gif)





![]() would have been negative but in
the argument above the interval
would have been negative but in
the argument above the interval
![]() would have to have been written in the other order.
This would have meant that our formula had
would have to have been written in the other order.
This would have meant that our formula had
![]() .
In both cases this amounts to the formula
.
In both cases this amounts to the formula
![]() or (see Chapter 3 for definitions of a number of ``standard''
distributions)
or (see Chapter 3 for definitions of a number of ``standard''
distributions)

![]() so that
so that
![]() .
Setting
.
Setting ![]() and solving
gives
and solving
gives ![]() so that
g-1(y) = ey. Then
so that
g-1(y) = ey. Then
![]() and
and
![]() .
Hence
.
Hence



![]() and Y=X1 (or in general any Xj).
and Y=X1 (or in general any Xj).
![]() the marginal density of
the marginal density of
![]() and use the
expression joint density for fX but
and use the
expression joint density for fX but
![]() is exactly the
usual density of
is exactly the
usual density of
![]() .
The adjective ``marginal'' is just there to
distinguish the object from the joint density of X.
.
The adjective ``marginal'' is just there to
distinguish the object from the joint density of X.

![]() .
Formally we find functions
.
Formally we find functions
![]() and define
and define