


Postscript version of this file
STAT 450 Lecture 4
Reading for Today's Lecture:
Sections 1, 2 and 3 of Chapter 2. Sections 1 and 2 of Chapter 4.
Goals of Today's Lecture:
- Define independent events and random variables.
- Define joint and marginal densities.
- Define conditional probabilities, conditional densities.
Last time: We introduced distribution theory
- X has known distribution
- Y=g(X) -- problem is to find distribution of Y.
We derived change of variables method:
- Requires g one to one.
- Solve y=g(x) for x to get x=h(y); technically,
h is just g-1, the inverse function of g.
- Get
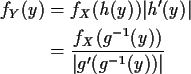
Note: Last time I did only the case g increasing
where  would be positive. Thus my derivation misses the
absolute sign needed if g is decreasing.
would be positive. Thus my derivation misses the
absolute sign needed if g is decreasing.
Reading for Today's Lecture: Chapter 4 sections
1, 2 and 3. Chapter 1 section 3.6.
Goals of Today's Lecture:
- Define independent events and random variables.
- Describe relation between joint and marginal densities.
- Describe structure of joint cdf and density of independent
random variables.
- Define conditional probabilities.
- Motivate definition of conditional density.
Today's notes
Long term plan:
The general multivariate problem has
and our goal is to compute fY from fX.
Case 1: If q>p then Y will not have a density
for ``smooth'' g. Y will have a singular or discrete
distribution.
This sort of problem is rarely
of real interest. (However, variables of interest often have a
singular distribution - this is almost always true of the set of residuals
in a regression problem.)
Case 2 If q=p then we will be able to use a
change of variables formula.
Case 3: If q < p we will try a two step process,
first applying a change of variables formula then a technique called
marginalization.
Before we do any of this we develop mathematical tools to manipulate
joint densities: independence, marginal densities, conditional densities.
Independence, conditional distributions
In the examples so far the density for X has been specified
explicitly. In many situations, however, the process of modelling
the data leads to a specification in terms of marginal and conditional
distributions.
Definition: Events A and B are independent if
(Note the notation: AB is the event that both A and B happen. It
is also written  .)
.)
Definition: Events Ai,
 are independent if
are independent if
for any set of distinct indices
 between 1 and p.
between 1 and p.
Example: p=3
You need all these equations to be true for independence!
Definition: Random variables X and Y are
independent if
for all A and B.
Definition: Random variables
 are
independent if
are
independent if
for any choice of
 .
.
Theorem 1
- 1.
- If X and Y are independent then
FX,Y(x,y) = FX(x)FY(y)
for all x,y
- 2.
- if X and Y have densities fX and fY and X and Y are independent
then
(X,Y) has density
- 3.
- if X and Y are independent and (X,Y) has density f(x,y)then X has a density, say fX, and Y has a density, say fY such
that for all x and y
- 4.
- If
FX,Y(x,y) = FX(x)FY(y)
for all x,y then X and Y are independent.
- 5.
- If (X,Y) has density f(x,y) and there are functions
g(x) and h(y) such that
f(x,y) = g(x) h(y)
for all (well technically almost all) (x,y) then
X and Y are independent and they each have a density
given by
X and Y are independent and they each have a density
given by
and
Proof:
- 1.
- Since X and Y are independent so are the events
 and
and  ;
hence
;
hence
- 2.
- For any A and B we have

If we define
g(x,y) = fX(x)fY(y) then we have proved that
for

Our definition of density is that g is the density if this
formula holds for all (Borel) C. I will not discuss this
proof in class but here is the key idea:
To prove that g is the joint density of (X,Y) we need only
prove that this integral formula is valid for an arbitrary Borel set
C, not just a rectangle
 .
This is proved via a
monotone class argument. You prove that the collection of sets Cfor which the identity holds has closure properties which guarantee that
this collection includes the Borel sets.
.
This is proved via a
monotone class argument. You prove that the collection of sets Cfor which the identity holds has closure properties which guarantee that
this collection includes the Borel sets.
- 3.
- For clarity suppose X and Y are real valued.
In assignment 2 I have asked you to prove that the existence of fX,Yimplies that fX and fY exist (and are given by the marginal density
formula).
Then for any sets A and B

Since
 we see that for any sets
A and B
we see that for any sets
A and B
It follows (via measure theory) that the quantity in [] is 0
(for almost every pair (x,y)).
- 4.
- This is proved via another monotone class argument.
- 5.
-

Take B=R1 to see that
where
 .
From the definition of density
we see that c1 g is the density of X.
Since
.
From the definition of density
we see that c1 g is the density of X.
Since
 we see that
we see that
 so that
so that
 .
A similar argument works for Y.
.
A similar argument works for Y.
Theorem 2
If

are independent and
Yi =
gi(
Xi) then

are independent.
Moreover,

and

are
independent.
Conditional probability
Def'n:
P(A|B) = P(AB)/P(B) provided
 .
.
Def'n: For discrete random variables X and Y the conditional
probability mass function of Y given X is

For absolutely continuous X the problem is that
P(X=x) = 0 for all
x so how can we define P(A| X=x) or
fY|X(y|x)?
The solution is to take a limit
If, for instance, X,Y have joint density fX,Y then with
 we have
we have

Divide the top and bottom by  and let
and let  tend to 0.
The denominator converges to fX(x) while the numerator converges to
tend to 0.
The denominator converges to fX(x) while the numerator converges to
So we define the conditional cdf of Y given X=x to be
Differentiate with respect to y to get the definition of the
conditional density of Y given X=x namely
fY|X(y|x) = fX,Y(x,y)/fX(x)
or in words ``conditional = joint/marginal''.
Marginalization
Now we turn to multivariate problems. The simplest version has
 and Y=X1 (or in general any Xj).
and Y=X1 (or in general any Xj).
Theorem 3
If
X has (joint) density

then

(with
q <
p) has a density
fY given by
We call
 the marginal density of
the marginal density of
 and use the
expression joint density for fX but
and use the
expression joint density for fX but
 is exactly the
usual density of
is exactly the
usual density of
 .
The adjective ``marginal'' is just there to
distinguish the object from the joint density of X.
.
The adjective ``marginal'' is just there to
distinguish the object from the joint density of X.
Example The function
f(x1,x2) = Kx1x21(x1> 0) 1(x2 >0) 1(x1+x2 < 1)
is a density for a suitable choice of K, namely the value of Kmaking
The integral is
so that K=24.
The marginal density of x1 is
which is the same as
This is a
 density.
density.
The general multivariate problem has
Case 1: If q>p then Y will not have a density
for ``smooth'' g. Y will have a singular or discrete distribution.
This sort of problem is rarely
of real interest. (However, variables of interest often have a
singular distribution - this is almost always true of the set of residuals
in a regression problem.)
Case 2 If q=p then we will be able to use a
change of variables
formula which generalizes the one derived above for the
case p=q=1. (See below.)
Case 3: If q < p we will try a two step process.
In the first step we pad out Y
by adding on p-q more variables (carefully chosen)
and calling them
 .
Formally we find functions
.
Formally we find functions
 and define
and define
If we have chosen the functions carefully we will find that
 satisfies the conditions for applying
the change of variables formula from the previous case.
Then we apply that case to compute fZ. Finally we marginalize
the density of Z to find that of Y:
satisfies the conditions for applying
the change of variables formula from the previous case.
Then we apply that case to compute fZ. Finally we marginalize
the density of Z to find that of Y:



Richard Lockhart
1999-09-14
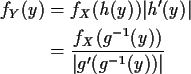
![]() would be positive. Thus my derivation misses the
absolute sign needed if g is decreasing.
would be positive. Thus my derivation misses the
absolute sign needed if g is decreasing.
![]() are independent if
are independent if


![]() are
independent if
are
independent if



![]() .
.



![]() and Y=X1 (or in general any Xj).
and Y=X1 (or in general any Xj).
![]() the marginal density of
the marginal density of
![]() and use the
expression joint density for fX but
and use the
expression joint density for fX but
![]() is exactly the
usual density of
is exactly the
usual density of
![]() .
The adjective ``marginal'' is just there to
distinguish the object from the joint density of X.
.
The adjective ``marginal'' is just there to
distinguish the object from the joint density of X.

![]() .
Formally we find functions
.
Formally we find functions
![]() and define
and define