Postscript version of this file

STAT 450 Lecture 5

Reading for Today's Lecture: Chapter 2

Goals of Today's Lecture:

• Define marginal densities.

• Introduce change of variables formula.

• Define multivariate normal distribution.

Last time: We defined:

• independent events.
• independent random variables.
• conditional probabilities.
• conditional discrete densities.

We stated theorem saying independence is ``equivalent'' to factorization of either joint density or joint cdf.

We began to define conditional densities.

Reading for Today's Lecture: Chapter 4 sections 1, 2 and 3. Chapter 1 section 3.6.

Today's notes

Defining a conditional density

We will define the conditional density of Y given X=x to be

$$f_{Y\vert X}(y\vert x) = \frac{\partial}{\partial y} P(Y \le y\vert X=x)$$

and we will define

$$P(Y \le y\vert X=x) = \lim_{\delta x \to 0} P(Y \le y\vert x \le X \le x+\delta x) \, .$$

If X,Y have joint density f_X,Y then with $A=\{ Y \le y\}$ we have
$$\begin{align*}P(A\vert x \le X \le x+\delta x) & = \frac{P(A \cap x \le X \le x+... ...{x+\delta x} f_{X,Y}(u,v)dudv }{ \int_x^{x+\delta x} f_X(u) du } \end{align*}$$
Divide the top and bottom by $\delta x$ and let $\delta x$ tend to 0. The denominator converges to f_X(x) while the numerator converges to

$$\int_{-\infty}^y f_{X,Y}(x,v) dv$$

So we define the conditional cdf of Y given X=x to be

$$P(Y \le y \vert X=x) = \frac{ \int_{-\infty}^y f_{X,Y}(x,v) dv }{ f_X(x) }$$

Differentiate with respect to y to get the definition of the conditional density of Y given X=x namely

f_Y|X(y|x) = f_X,Y(x,y)/f_X(x)

or in words ``conditional = joint/marginal''.

Marginalization

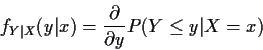
Now we turn to multivariate problems. The simplest version has $X=(X_1,\ldots,X_p)$ and Y=X₁ (or in general any X_j).

Theorem 1   If X has (joint) density $f(x_1,\ldots,x_p)$ then $Y=(X_1,\ldots,X_q)$ (with q < p) has a density f_Y given by

$$f_{X_1,\ldots,X_q}(x_1,\ldots,x_q) = \int_{-\infty}^\infty \c... ...-\infty}^\infty f(x_1,x_2,\ldots,x_p) \, dx_{q+1} \ldots dx_p$$

We call $f_{X_1,\ldots,X_q}$ the marginal density of $X_1,\ldots,X_q$ and use the expression joint density for f_X but $f_{X_1,\ldots,X_q}$ is exactly the usual density of $(X_1,\ldots,X_q)$. The adjective ``marginal'' is just there to distinguish the object from the joint density of X.

Example The function

f(x₁,x₂) = Kx₁x₂1(x₁> 0) 1(x₂ >0) 1(x₁+x₂ < 1)

is a density for a suitable choice of K, namely the value of Kmaking

$$P(X\in R^2) = \int_{-\infty}^\infty \int_{-\infty}^\infty f(x_1,x_2)\, dx_1\, dx_2 = 1 \, .$$

The integral is

$$\begin{eqnarray*}K \int_0^1 \int_0^{1-x_1} x_1 x_2 \, dx_1\, dx_2 & = & K \int_0... ...1(1-x_1)^2 \, dx_1 /2 \\ & = & K(1/2 -2/3+1/4)/2 \\ & = & K/24 \end{eqnarray*}$$

so that K=24.

The marginal density of x₁ is

$$f_{X_1}(x_1) = \int_{-\infty}^\infty 24 x_1 x_2 1(x_1> 0) 1(x_2 >0) 1(x_1+x_2 < 1)\, dx_2$$

which is the same as

$$f_{X_1}(x_1) = 24 \int_0^{1-x_1} x_1 x_2 1(x_1> 0) 1(x_1 < 1) \, dx_2 = 12 x_1(1-x_1)^2 1(0 < x_1 < 1)$$

This is a $\mbox{Beta}(2,3)$ density.

The general multivariate problem has

$$Y=(Y_1,\ldots,Y_q) = ( g_1(X_1,\ldots,X_p), \ldots, g_q(X_1,\ldots,X_p))$$

Case 1: If q>p then Y will not have a density for ``smooth'' g. Y will have a singular or discrete distribution. This sort of problem is rarely of real interest. (However, variables of interest often have a singular distribution - this is almost always true of the set of residuals in a regression problem.)

Case 2 If q=p then we will be able to use a change of variables formula which generalizes the one derived above for the case p=q=1. (See below.)

Case 3: If q < p we will try a two step process. In the first step we pad out Y by adding on p-q more variables (carefully chosen) and calling them $Y_{q+1},\ldots,Y_p$. Formally we find functions $g_{q+1}, \ldots,g_p$ and define

$$Z=(Y_1,\ldots,Y_q,g_{q+1}(X_1,\ldots,X_p),\ldots,g_p(X_1,\ldots,X_p))$$

If we have chosen the functions carefully we will find that $g=(g_1,\ldots,g_p)$ satisfies the conditions for applying the change of variables formula from the previous case. Then we apply that case to compute f_Z. Finally we marginalize the density of Z to find that of Y:

$$f_Y(y_1,\ldots,y_q) = \int_{-\infty}^\infty \cdots \int_{-\in... ...f_Z(y_1,\ldots,y_q,z_{q+1},\ldots,z_p) \, dz_{q+1} \ldots dz_p$$

Change of Variables

Suppose $Y=g(X) \in R^p$ with $X\in R^p$ having density f_X. Assume the g is a one to one (``injective") map, that is, g(x₁) = g(x₂) if and only if x₁ = x₂. Then we find f_Y as follows:

Step 1: Solve for x in terms of y: x=g^-1(y).

Step 2: Remember the following basic equation

f_Y(y) dy =f_X(x) dx

and rewrite it in the form

$$f_Y(y) = f_X(g^{-1}(y)) \frac{dx}{dy}$$

It is now a matter of interpreting this derivative $\frac{dx}{dy}$ when p>1. The interpretation is simply

$$\frac{dx}{dy} = \left\vert \mbox{det}\left(\frac{\partial x_i}{\partial y_j}\right)\right\vert$$

which is the so called Jacobian of the transform. An equivalent formula inverts the matrix and writes

$$f_Y(y) = \frac{f_X(g^{-1}(y))}{ \left\vert\frac{dy}{dx}\right\vert}$$

This notation means

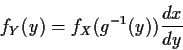
$$\left\vert\frac{dy}{dx}\right\vert = \left\vert \mbox{det} \... ...rac{\partial y_p}{\partial x_p} \end{array} \right]\right\vert$$

but with x replaced by the corresponding value of y, that is, replace x by g^-1(y).

Example: The density

$$f_X(x_1,x_2) = \frac{1}{2\pi} \exp\left\{ -\frac{x_1^2+x_2^2}{2}\right\}$$

is called the standard bivariate normal density. Let Y=(Y₁,Y₂) where $Y_1=\sqrt{X_1^2+X_2^2}$ and Y₂ is the angle (between 0 and $2\pi$) in the plane from the positive x axis to the ray from the origin to the point (X₁,X₂). In other words, Y is X in polar co-ordinates.

The first step is to solve for x in terms of y which gives

$$\begin{eqnarray*}X_1 & = & Y_1 \cos(Y_2) \\ X_2 & = & Y_1 \sin(Y_2) \end{eqnarray*}$$

so that in formulas

$$\begin{eqnarray*}g(x_1,x_2) & = & (g_1(x_1,x_2),g_2(x_1,x_2)) \\ & = & (\sqrt{x... ..._2) & y_1 \cos(y_2) \end{array}\right) \right\vert \\ & = & y_1 \end{eqnarray*}$$

It follows that

$$f_Y(y_1,y_2) = \frac{1}{2\pi}\exp\left\{-\frac{y_1^2}{2}\right\}y_1 1(0 \le y_1 < \infty) 1(0 \le y_2 < 2\pi )$$

Next problem: what are the marginal densities of Y₁ and Y₂? Note that f_Y can be factored into f_Y(y₁,y₂) = h₁(y₁)h₂(y₂) where

$$h_1(y_1) = y_1e^{-y_1^2/2} 1(0 \le y_1 < \infty)$$

and

$$h_2(y_2) = 1(0 \le y_2 < 2\pi )/ (2\pi)$$

It is then easy to see that

$$f_{Y_1}(y_1) = \int_{-\infty}^\infty h_1(y_1)h_2(y_2) \, dy_2 = h_1(y_1) \int_{-\infty}^\infty h_2(y_2) \, dy_2$$

which says that the marginal density of Y₁ must be a multiple of h₁. The multiplier needed will make the density integrate to 1 but in this case we can easily get

$$\int_{-\infty}^\infty h_2(y_2) \, dy_2 = \int_0^{2\pi} (2\pi)^{-1} dy_2 = 1$$

so that

$$f_{Y_1}(y_1) = y_1e^{-y_1^2/2} 1(0 \le y_1 < \infty)$$

which is special Weibull density also called a Rayleigh distribution. Similarly

$$f_{Y_2}(y_2) = 1(0 \le y_2 < 2\pi )/ (2\pi)$$

which is the Uniform($(0,2\pi)$ density. You should be able to check that W=Y₁²/2 has a standard exponential distribution. You should also know that by definition U=Y₁² has a $\chi^2$ distribution on 2 degrees of freedom and be able to find the $\chi^2_2$ density.

Note: This is an example of the general theorem I wrote down: when a joint density factors into a product you will always see the phenomenon above -- the factor involving the variable not be integrated out will come out of the integral and so the marginal density will be a multiple of the factor in question. This happens when and only when the two parts of random vector are independent.