Postscript version of this file

STAT 450 Lecture 6

Reading for Today's Lecture: Section 5 of Chapter 4. Chapter 6 section 4.

Goals of Today's Lecture:

• Learn properties of independence
• Define Multivariate Normal Dist.
• Do 1 sample normal distribution theory.

Last time

We derived the change of variables formula:

$$f_Y(y) = f_X(x) \left\vert \frac{dx}{dy}\right\vert$$

where x is replaced by the formula for x in terms of yand the second term means the absolute value of the determinant of the matrix full of all possible derivatives of x_i with respect to y_j.

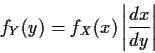
We showed that if (X,Y) has a density f_X,Y(x,y) then X has (marginal) density

$$f_X(x) = \int_{-\infty}^\infty f_{X,Y}(x,y) dy$$

The jargon ``marginal'' just serves to emphasize that we are also thinking about the ``joint'' density f_X,Y.

Today's notes

The Multivariate Normal Distribution

Def'n: $Z \in R^1 \sim N(0,1)$ iff

$$f_Z(z) = \frac{1}{\sqrt{2\pi}} e^{-z^2/2}$$

Def'n: $Z \in R^p \sim MVN(0,I)$ iff $Z=(Z_1,\ldots,Z_p)^t$ (a column vector for later use) with the Z_i independent and each $Z_i\sim N(0,1)$.

In this case according to our theorem
$$\begin{align*}f_Z(z_1,\ldots,z_p) &= \prod \frac{1}{\sqrt{2\pi}} e^{-z_i^2/2} \\ & = (2\pi)^{-p/2} \exp\{ -z^t z/2\} \end{align*}$$
where the superscript t denotes matrix transpose.

[Notes on linear algebra.]

Def'n: $X\in R^p$ has a multivariate normal distribution if it has the same distribution as $AZ+\mu$ for some $\mu\in R^p$, some $p\times p$ matrix of constants A and $Z\sim MVN(0,I)$.

If the matrix A is singular then X will not have a density. If A is invertible then we can derive the multivariate normal density by the change of variables formula:

$$X=AZ+\mu \Leftrightarrow Z=A^{-1}(X-\mu)$$

$$\frac{\partial X}{\partial Z} = A \qquad \frac{\partial Z}{\partial X } = A^{-1}$$

So
$$\begin{align*}f_X(x) &= f_Z(A^{-1}(x-\mu)) \vert \det(A^{-1})\vert \\ &= \frac{... ...p\{-(x-\mu)^t (A^{-1})^t A^{-1} (x-\mu)/2\} }{ \vert\det{A}\vert } \end{align*}$$
Now define $\Sigma=AA^t$ and notice that

$$\Sigma^{-1} = (A^t)^{-1} A^{-1} = (A^{-1})^t A^{-1}$$

and

$$\det \Sigma = \det A \det A^t = (\det A)^2$$

Thus

$$f_X(x) = (2\pi)^{-p/2} (\det\Sigma)^{-1/2} \exp\{ -(x-\mu)^t \Sigma^{-1} (x-\mu) /2 \}$$

which is called the $MVN(\mu,\Sigma)$ density. Notice that the density is the same for all A such that $AA^t=\Sigma$. This justifies the notation $MVN(\mu,\Sigma)$.

For which vectors $\mu$ and matrices $\Sigma$ is this a density? Any $\mu$ will work but if $x \in R^p$ then
$$\begin{align*}x^t \Sigma x & = x^t A A^t x \\ &= (A^t x)^t (A^t x) \\ & = \sum_1^p y_i^2 \\ &\ge 0 \end{align*}$$
where y=A^t x. The inequality is strict except for y=0 which is equivalent to x=0. Thus $\Sigma$ is a positive definite symmetric matrix. Conversely, if $\Sigma$ is a positive definite symmetric matrix then there is a square invertible matrix A such that $AA^t=\Sigma$ so that there is a $MVN(\mu,\Sigma)$ distribution. (The matrix A can be found via the Cholesky decomposition, for example.)

More generally we say that X has a multivariate normal distribution if it has the same distribution as $AZ+\mu$ where now we remove the restriction that A be non-singular. When A is singular X will not have a density because there will exist an a such that $P(a^t X = a^t \mu) =1$, that is, so that X is confined to a hyperplane. It is still true, however, that the distribution of X depends only on the matrix $\Sigma=AA^t$ in the sense that if AA^t = BB^t then $AZ+\mu$ and $BZ+\mu$ have the same distribution.

Properties of the MVN distribution

1: All margins are multivariate normal: if

$$X = \left[\begin{array}{c} X_1\\ X_2\end{array} \right]$$

$$\mu = \left[\begin{array}{c} \mu_1\\ \mu_2\end{array} \right]$$

and

$$\Sigma = \left[\begin{array}{cc} \Sigma_{11} & \Sigma_{12} \\ \Sigma_{21} & \Sigma_{22} \end{array} \right]$$

then $X\sim MVN(\mu,\Sigma)$ implies that $X_1\sim MVN(\mu_1,\Sigma_{11})$.

2: All conditionals are normal: the conditional distribution of X₁given X₂=x₂ is $MVN(\mu_1+\Sigma_{12}\Sigma_{22}^{-1} (x_2-\mu_2),\Sigma_{11}-\Sigma_{12}\Sigma_{22}^{-1}\Sigma_{21})$

3: $MX+\nu \sim MVN(M\mu+\nu, M \Sigma M^t)$. That is, an affine transformation of a Multivariate Normal is normal.

Normal samples: Distribution Theory

Theorem 1   Suppose $X_1,\ldots,X_n$ are independent $N(\mu,\sigma^2)$ random variables. (That is each satisfies my definition above in 1 dimension.) Then

1.

The sample mean $\bar X$ and the sample variance s² are independent.

2.

$n^{1/2}(\bar{X} - \mu)/\sigma \sim N(0,1)$

3.

$(n-1)s^2/\sigma^2 \sim \chi^2_{n-1}$

4.

$n^{1/2}(\bar{X} - \mu)/s \sim t_{n-1}$

Proof: Let $Z_i=(X_i-\mu)/\sigma$. Then $Z_1,\ldots,Z_p$ are independent N(0,1) so $Z=(Z_1,\ldots,Z_p)^t$ is multivariate standard normal. Note that $\bar{X} = \sigma\bar{Z}+\mu$ and $s^2 = \sum(X_i-\bar{X})^2/(n-1) = \sigma^2 \sum(Z_i-\bar{Z})^2/(n-1)$Thus

$$\frac{n^{1/2}(\bar{X}-\mu)}{\sigma} = n^{1/2}\bar{Z}$$

$$\frac{(n-1)s^2}{\sigma^2} = \sum(Z_i-\bar{Z})^2$$

and

$$T=\frac{n^{1/2}(\bar{X} - \mu)}{s} = \frac{n^{1/2} \bar{Z}}{s_Z}$$

where $(n-1)s_Z^2 = \sum(Z_i-\bar{Z})^2$.

Thus we need only give a proof in the special case $\mu=0$ and $\sigma=1$.